
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Понятие кодирования цифровой информации
Вопросы и упражнения
1.1. Дайте определение цифрового сигнала.
1.2. Назовите достоинства обработки радиотехнических сигналов цифровыми методами.
1.3. Что подразумевается под понятием «серия цифровых микросхем»?
1.4. Дайте определение АЦП и ЦАП.
1.5. Переведите числа (А) = 177 и (В) = 53 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
1.6. Определите правила выполнения арифметических операций с двоичными числами.
1.7. Напишите правила выполнения операции суммирования по модулю два.
Лекция 2. Логические функции и тождества
Кодирование цифровой информации. Двоично-десятичные коды. Логические функции двух аргументов и двухвходовые логические элементы. Функционально полный набор элементов. Элементы Пирса и Шеффера
Цифровая информация может быть представлена определенным набором символов. Этот процесс носит название кодирования, а состав символов для конкретной цифровой информации является алфавитом данного кода.
Все коды можно классифицировать на две самостоятельные группы. Коды, использующие все возможные комбинации, – не избыточные коды. И вторая группа – это коды, в которых используется лишь часть всех возможных комбинаций, или избыточные коды. Оставшиеся комбинации несут в себе информацию об ошибках в системах обработки и передачи данных [13, 14].
Указанные коды классифицируются на равномерные и неравномерные, взвешенные и не взвешенные и т.д. Например, натуральный двоичный код является взвешенным кодом, поскольку каждый разряд имеет свой вес, равный степени числа 2.
Существуют различные взвешенные двоично-десятичные коды, например: 8421, 7421, 5311, 5221, 4421, 4321, 3331.
Для определения символов в различных кодах введено обобщенное правило:
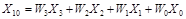 , (2.1)
, (2.1)
где символы WЗ... W0 являются постоянными весовыми коэффициентами соответствующего кода; символы ХЗ... ХО – двоичные цифры 1 или 0. В соответствии с формулой в табл. 2.1 приведены комбинации.
Таблица 2.1
| X10 | Не взвешенный | ||||
| 0 1 2 3 4 | 0000 0001 0010 0011 0100 | 0000 0001 0010 0011 0110 | 0000 0001 0010 0011 0110 | 0000 0001 0010 0011 0100 | 0000 0001 0010 0101 1000 |
Окончание табл. 2.1
| 5 6 7 8 9 | 0101 0110 0111 1000 | 0111 1010 1011 1110 1111 | 0111 1110 1111 1100 1101 | 1011 1100 1101 1110 1111 | 0111 1010 1101 1110 1111 |
2.2 Представление операндов
в прямом, обратном и дополнительном кодах
При выполнении арифметических операций с двоичными числами операнды представляются специальными кодами, содержащими информацию о знаке числа. Под знаковый, как правило, отводят старший двоичный разряд числа: если он равен нулю – число положительное, единице – отрицательное. Простое добавление знакового разряда слева к двоичному представлению числа означает, что число представлено в прямом коде. Числа с одинаковым знаком в прямом коде складываются довольно просто по правилам арифметики. Однако сложение чисел с разными знаками (т.е. фактически реализация операции вычитания) выполняется сложнее. Сложим, например, два числа 1210 и –710:
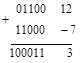 .
.
Как видно, вместо того, чтобы получить 5, в результате мы получили бессмысленную информацию. Более простым является вычитание чисел в обратном коде. Этот код (для отрицательных чисел) получается инвертированием всех разрядов прямого кода, кроме знакового. Попробуем повторить предыдущее действие, используя обратный код:
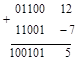 .
.
Как видно, для получения искомого результата разряд, возникающий в результате переноса из старшего разряда результата, необходимо прибавить к младшему разряду результата. В этом заключается правило вычитания чисел в обратном коде. Неудобным является то, что правила сложения и вычитания (т.е. сложения чисел с разными знаками) в обратном коде являются различными. Для унификации правил вводится так называемый дополнительный код числа: для положительных чисел его представление совпадает с прямым кодом, для отрицательных берется обратный код, к младшему разряду которого добавляется единица.
Разряд, возникающий в результате переноса из старших разрядов, просто игнорируется.
| <== предыдущая страница | | | следующая страница ==> |
| Краткие сведения о системах счисления | | | Основные логические функции |
Дата добавления: 2014-02-26; просмотров: 405; Нарушение авторских прав

Мы поможем в написании ваших работ!