Студопедия

Главная страница Случайная лекция


Мы поможем в написании ваших работ!

Порталы:

БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика



Мы поможем в написании ваших работ!




Основные логические функции

Читайте также:
  1. I. Основные принципы и идеи философии эпохи Просвещения.
  2. II. ОСНОВНЫЕ ФАКТОРЫ РАДИАЦИОННОЙ ОПАСНОСТИ И МЕДИЦИНСКИЕ ПОСЛЕДСТВИЯ ОТ ИХ ВОЗДЕЙСТВИЯ НА ОРГАНИЗМ.
  3. II. РАСПРЕДЕЛЕНИЕ ЛЕКАРСТВЕННЫХ СРЕДСТВ В ОРГАНИЗМЕ. БИОЛОГИЧЕСКИЕ БАРЬЕРЫ. ДЕПОНИРОВАНИЕ
  4. III. Основные политические идеологии современности.
  5. III. Предмет, метод и функции философии.
  6. IV. По функции различают мышцы: сгибатели и разгибатели, отводящие и приводящие и вращатели.
  7. IV.5. Основные тенденции развития позднефеодальной ренты (вторая половина XVII—XVIII в.)
  8. V. АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД И МАССИВОВ. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД
  9. V6. ОСНОВНЫЕ СЕМАНТИКО-СТИЛЕВЫЕ ОСОБЕННОСТИ ХУДОЖЕСТВЕННОЙ ЛИТЕРАТУРЫ. ОБРАЗ АВТОРА
  10. Акцентологические нормы

Математический аппарат, используемый при проектировании ЦУ, основан на алгебре-логике (булевой алгебре). Основными функциями булевой алгебры являются дизъюнкция, конъюнкция и инверсия. Дадим их краткие определения. Дизъюнкция – это логическое сложение (обозначается знаком V и читается ИЛИ). Конъюнкция – логическое умножение (обозначается знаком L и читается И). Инверсия – отрицание (обозначается чертой над аргументом и читается НЕ).

Данные операции выполняются по вполне определенным правилам, а именно:

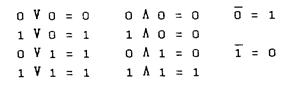
На основе этих постулатов построены тождества булевой алгебры, приведенные в табл. 2.2.

Таблица 2.2

Логические тождества

№ п/п Название Аналитическая запись
1. Закон сложения с 1 Х V X = 1
2. Закон сложения с нулем X V 0= X
3. Законы тавтологии X V X = X
4. X L X = X
5. Закон умножения на 1 X L 1= X
6. Закон умножения на нуль X L 0 = 0
7. Законы дополнительности X V X = X
8. X L X = X

Окончание табл.2.2

9. Закон двойного отрицания X = X
10. Сочетательные зоны X1 V X2 V X0 = X2 (X1 V X0)
11. (X2 L X1) L X0 = X2 L (X1 L X0)
12. Переместительные законы X1 V X0 = X0 V X1
13. X1L X0 = X0X1
14. Распределительные законы (X1 V X0) L X2 = X1 L X2 V X0 L X2
15. X2 L X1 V X0 = (X2V X0) L (X1 V X0)
16. Теорема Моргана X1 L X0 = X0 L X1
17. X1 L X0 = X0 V X1

 

Данные тождества являются основой при построении цифровых устройств, реализующих различные логические функции

Одна из часто употребляемых логических функций носит название суммирование по модулю 2 и обозначается знаком Å и выполняется по следующим правилам:

0 Å 0 = 0 0 Å 1 = 1 1 Å 0 = 1 1 Å 1 = 0

Замечательной особенностью алгебры-логики является ограниченное число возможных функций. Поскольку каждый аргумент может принимать лишь одно из двух значений (0 или 1), то число возможных комбинаций n аргументов составит:

.

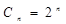Такому числу комбинаций будет соответствовать следующее число логических функций:

.

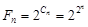Например, когда число аргументов n= 2, получим 16 различных логических функций.

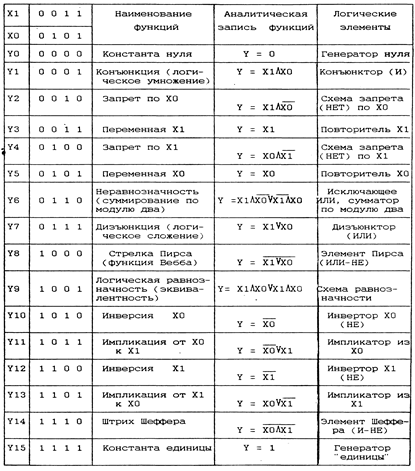
В табл. 2.3 приведены все возможные логические функции двух аргументов. С помощью этих функций можно построить сколь угодно сложные функции многих аргументов, а на их основе – цифровые устройства от логических элементов до микропроцессорных систем.

Таблица 2.3

Логические функции двух аргументов

<== предыдущая страница | следующая страница ==>
Понятие кодирования цифровой информации | Функционально полный набор

Дата добавления: 2014-02-26; просмотров: 1058; Нарушение авторских прав



Мы поможем в написании ваших работ!
lektsiopedia.org - Лекциопедия - 2013 год. | Страница сгенерирована за: 0.003 сек.