Функционально полный набор

Простейшие логические элементы

Выполнение основных логических функций булевой алгебры осу­ществляется логическими элементами, условное изображение которых приведено на рис. 2.1. Для отображения функционирования элементов составляются таблицы истинности, которые также приведены на рис. 2.1. Таблицы отражают однозначную связь между состояниями входов и выходов элементов соответственно.

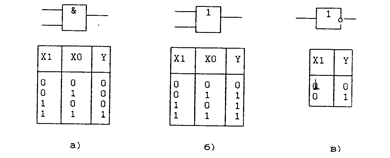
Рис.2.1. Условные графические обозначения и таблицы
истинности конъюнктора (а), дизъюнктора (б), инвертора (в)

Из таблицы 2.3. видно, что любую функцию можно выразить через три основные функции булевой алгебры. Это, в свою очередь, позволяет реализовать многовходовые элементы на основе двухвходовых.

Набор функций, достаточный для построения любой сколь угодно cложной функции, называется функционально-полной системой логических функций, а соответствующий набор элементов – функционально-полным набором логических элементов (ФПН). ФПН являются наборы, состоящие из конъюнктора, дизъюнктора и инвертора. Такой набор может состоять из двух элементов или даже одного. Примерами могут служить представленные на рис.2.2 элементы Пирса и Шеффера, последний из которых является базисным элементом цифровых интегральных микросхем, выполненных на основе транзисторно-транзисторной логики (ТТЛ).

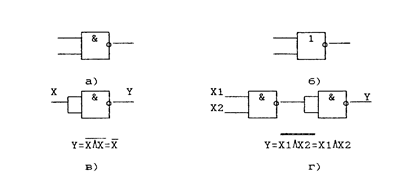
Рис.2.2. Элемент Шеффера (И-НЕ) (а), элемент Пирса (ИЛИ-НЕ) (б),
реализация на элементах Шеффера инвертора (в) и конъюнктора (г)

Отметим, что элементы Пирса и Шеффера являются двухступенчатыми логическими элементами, т.к. каждый выполняет две простые функции.

Дата добавления: 2014-02-26; просмотров: 985; Нарушение авторских прав

Мы поможем в написании ваших работ!