Псевдодальномерный метод ОМС по СНС

В дальномерном методе дистанция от спутника до потребителя определяется как D_i=C*t_i (2.10)

Где: t_i = tизлi- tпрi – время распространения сигнала от i спутника до потребителя.

tизлi – момент излучения сигнала i спутником, сообщается спутником.

tпрi – момент приема сигнала от i спутника, фиксируемый по часам приемоиндикатора.

Очевидно, что степень согласования шкал времени спутников и приемоиндикаторов должна быть высокой (не хуже 2 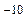). Технически возможна степень согласования 10 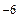с.

Для решения проблемы в систему уравнений (2.10) вводится еще одна неизвестная δt-невязка шкал времени спутника и приемоиндикатора (ПИ), которая принимается общей для всех спутников; при этом уравнение (2.10) приводится к виду: D_i=C*(t_i+ δt ) (2.11)

i=1,2,3 – плоскость (j,l,δt) 2-D позиционирование

i=1,2,3,4 – пространство (j,l,H,δt) – 3-D позиционирование

Для получения по уравнению (2.11) географических координат дистанция до i-го спутника выражается как диагональ параллелограмма

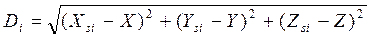i=1,2,3,4 (2.12)

Где: X_si, Y_si, Z_si – прямоугольные геоцентрические координаты спутника -(известны).

X,Y,Z - неизвестные геоцентрические координаты потребителя

Для перехода от прямоугольных координат к географическим используются известные соотношения:

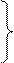X=[N+H]cosjcosl

Y=[N+H]cosjsinl (2.13)

Z=[N(1-e²)+H]sinj

Где: N – радиус кривизны принятого референт – эллипсоида или геометрическая модель земли, а применительно к картографии – система координат.

Н – высота наблюдателя

e – эксцентриситет принятого эллипсоида

Система (2.13) подставляется в каждое из уравнений (2.12) которое в свою очередь подставляется в левые части системы (2.11), в результате получаем систему четырех уравнений с четырьмя неизвестными j,l,H,δt.

Дата добавления: 2014-08-09; просмотров: 435; Нарушение авторских прав

Мы поможем в написании ваших работ!