
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МОДЕЛИ И МЕТОДЫ ПОДДЕРЖКИ ПРОЦЕССА АНАЛИЗА РИСКОВ ПРОЕКТА
2.1. ОСНОВНЫЕ ЗАДАЧИ АНАЛИЗА РИСКОВ
Анализ литературных источников показал, что в настоящее время отсутствуют достаточно эффективные методы и инструментальные средства поддержки этапа анализа рисков проекта при нечетких проектных данных. В связи с этим ниже рассматриваются теоретические и методологические вопросы построения эффективных алгоритмов анализа рисков проекта, которые столь необходимы для успешного выполнения сложных наукоемких проектов и поэтому подлежат изучению.
На этапе анализа рисков проекта предполагается, что полный исходный перечень (список) потенциальных рисковых событий (рисков) уже определен. Для этих целей существуют известные и хорошо себя зарекомендовавшие методы, которые позволяют менеджерам проекта решить эту трудно формализуемую задачу методом мозгового штурма и коллективным принятием согласованных решений на основе следующих данных:
· детального описания проектируемого изделия (потенциальные рисковые события (ПРС) существенно зависят от специфики конкретного продукта);
· исторической информации (опыт, полученный в ходе выполнения аналогичного проекта, может существенно помочь идентификации рисков);
· результатов интервьюирования участников проекта (помогают идентифицировать новые и пропущенные риски).
Определенный таким способом список рисков для современных проектов имеет большую размерность (от нескольких десятков до нескольких сотен идентифицированных рисков). Управлять всеми рисками по ходу проекта в действительности не представляется возможным из-за чрезвычайно большой размерности задачи и ограниченности ресурсов реальных проектов. В связи с этим на практике следует выбирать из ранжированного списка рисков некоторую совокупность наиболее важных рисков и осуществлять их планирование, мониторинг и управление для снижения возможного ущерба характеристикам качества проекта. Однако выбор такой оптимальной совокупности контролируемых рисков представляет не простую задачу. Известные методы эту задачу позволяют решать для финансовых, организационных (временных) и технических рисков. При этом риски считаются аддитивными и их общие последствия на показатели проекта достаточно просто определяются экспертными методами.
При управлении же рисками качества программного проекта указанная задача ранжирования и выбора совокупности ПРС значительно усложняется тем, что отдельные риски связаны явно или неявно с характеристиками качества проекта, которые в свою очередь образуют иерархическую модель характеристик качества проекта с весовыми коэффициентами значимости. При этом в общем случае в программном проекте такая модель характеристик качества (в соответствии с планом проекта) постоянно изменяется по отдельным этапам и параллельно по ходу проекта изменяется исходный состав идентифицированных рисков и меняется их связность с характеристиками качества проекта. В этих условиях требуются уже такие методы анализа и ранжирования рисков, которые могут учитывать как нечеткие данные по рискам, так и сложный вид интегрированной модели характеристик качества проекта.
В учебном пособии ниже рассмотрено решение указанной задачи выбора квазиоптимального состава рисков проекта с использованием принципа декомпозиции, метода анализа иерархий, а также методов и моделей теории нечетких множеств. В этом случае этап формального анализа рисков содержит последовательное решение двух задач.
Задача 1 - определение степени влияния последствий каждого риска на обобщенный критерий качества проекта в условиях неопределенности мнений экспертов по рискам.
Задача 2 - выбор квазиоптимального состава контролируемых рисков качества проекта на основе принятия решений в условиях нечеткости проектных данных.
В следующих разделах учебного пособия рассматривается детальное решение этих задач.
2.2. МЕТОДЫ ОЦЕНИВАНИЯ ПОСЛЕДСТВИЙ РИСКОВ
2.2.1. ПОСТАНОВКА ЗАДАЧИ
Задача определения вектора влияния последствий рисков на обобщенный критерий качества проекта может быть сформулирована как задача формализации и согласования мнений экспертов по рискам о возможной (субъективной) степени влияния последствий рисковых событий на обобщенный критерий качества проекта. При этом для общего случая область определения такой задачи можно описать кортежем:
<R, H, fs, Ps , G, W(R), D>, (2.1)
где R – множество рисков, определенных на этапе идентификации рисков;
H – модель характеристик качества проекта;
fs – отображение R в H, т.е. оценка влияния последствий R на H;
Ps – структура предпочтений эксперта;
G – граф связности рисков качества проекта;
W(R) – вектор степеней влияния последствиймножества R на обобщенный критерий качества проекта;
D – наборалгоритмов,позволяющий определить W(R).
Анализ различных вариантов информационного состава (2.1) показывает, что в зависимости от типа модели качества проекта (независимые характеристики качества или иерархическая модель характеристик качества), вида экспертной информации при оценке степени влияния последствий рисков на характеристики качества (количественная или качественная), а также типа связности рисков (независимые, однозначно связные и субъективно связные) может быть использован ряд эффективных алгоритмов определения W(R). Укажем характеристики этих пяти алгоритмов.
Алгоритм D1 позволяет определять по стадиям ЖЦ проекта вектор W(R) на основе следующих исходных данных: модель Н задана множеством независимых (не связных) характеристик качества проекта; R– множество независимых рисков; f и Ps представлены экспертным способом на основе количественных оценок.
Алгоритм D2 отличается от D1 тем, что экспертные оценки по рискам (предпочтения экспертов) заданы вербальным способом.
Алгоритм D3 отличается от D1 и D2 тем, что модель Н представлена деревом характеристик качества в соответствии со структурой, регламентированной нормативно-методическими документами международного и государственного уровня.
Алгоритм D4 позволяет на основе данных, полученных при использовании одного из алгоритмов D1, D2, D3, учитывать дополнительную однозначную связность рисков по стадиям ЖЦ проекта.
Алгоритм D5, в отличие от D4, при определении по стадиям жизненного цикла (ЖЦ) проекта вектора W(R) учитывает субъективную связность потенциальных рисковых событий.
Рассмотрим на теоретическом и методологическом уровнях вопросы формализации и алгоритмизации решения задачи (2.1) посредством обоснования алгоритмов D1 – D5.
2.2.2. РЕШЕНИЕ ЗАДАЧИ ПРИ НЕЗАВИСИМЫХ ХАРАКТЕРИСТИКАХ КАЧЕСТВА И КОЛИЧЕСТВЕННОМ ЗАДАНИИ СТЕПЕНИ ВЛИЯНИЯ ПОСЛЕДСТВИЙ НЕЗАВИСИМЫХ РИСКОВ
2.2.2.1. ФОРМАЛИЗАЦИЯ ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ
Формальной основой алгоритма D1 является понятие нечеткого множества, которое впервые было сформулировано Л.Заде и послужило фундаментом для создания теории нечетких множеств, теоретические положения которой использованы при формализации и разработке методов и алгоритмов решения задачи.
Определение 2.1. Нечетким множеством 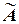 на универсальном множестве
на универсальном множестве 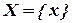 называется совокупность пар вида:
называется совокупность пар вида:
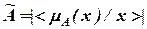 , (2.2)
, (2.2)
где 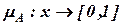 отображает хв единичный отрезок и называется функцией принадлежности множества
отображает хв единичный отрезок и называется функцией принадлежности множества 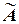 , а значение функции принадлежностиmA(х) для конкретного хÎХ называется степенью принадлежности.
, а значение функции принадлежностиmA(х) для конкретного хÎХ называется степенью принадлежности.
Согласно Л.Заде степень принадлежности является субъективной мерой того, насколько элемент хÎХсоответствует понятию, смысл которого формализуется нечетким множеством 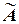 . С учетом введенного определения задача (2.1) может быть сформулирована следующим образом.
. С учетом введенного определения задача (2.1) может быть сформулирована следующим образом.
Пусть при планировании проекта выделены m несвязанных характеристик качества H={H1,H2,…,Hm}, на которые заданы ограничения в техническом задании. На этапе идентификации определен список из n потенциальных рисковых событий R={R1,R2,…,Rn}. Далее экспертным путем для каждого риска определена оценка 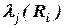 степени влияния последствий Riна характеристику качества Hj. Данные оценки могут формироваться из результатов экспертного опроса прямыми и косвенными методами.
степени влияния последствий Riна характеристику качества Hj. Данные оценки могут формироваться из результатов экспертного опроса прямыми и косвенными методами.
Прямые методы
Самым простым является прямой метод для одного эксперта по рискам. В этом случае эксперт оценивает в интервале [0,1] степень влияния последствий Ri на характеристику качества Hj и получает значения 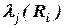 :
:
 . (2.3)
. (2.3)
Прямой метод для группы экспертов по рискам состоит в следующем: пусть имеется z экспертов по рискам, 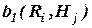 из которых на вопрос о значительности влияния последствий Ri на характеристику качества Hj ответили положительно, а другая часть
из которых на вопрос о значительности влияния последствий Ri на характеристику качества Hj ответили положительно, а другая часть 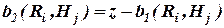 ответила на этот вопрос отрицательно, тогда принимается:
ответила на этот вопрос отрицательно, тогда принимается:
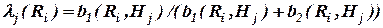 .(2.4)
.(2.4)
Прямые методы как для одного, так и для группы экспертов по рискам имеют один общий недостаток: свойственность человеку ошибаться (налет субъективизма).
Косвенные методы
Косвенные методы основаны на более осторожном использовании человека (эксперта) в качестве «измерительного прибора» и используются для снижения субъективного влияния на результаты определения оценки 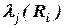 . Один из видов косвенных методов основан на процедуре построения функции принадлежности на основе количественного попарного сравнения степеней принадлежности. В зависимости от количества экспертов по рискам и способа задания предпочтительности мнений экспертов существует несколько алгоритмов формирования оценок
. Один из видов косвенных методов основан на процедуре построения функции принадлежности на основе количественного попарного сравнения степеней принадлежности. В зависимости от количества экспертов по рискам и способа задания предпочтительности мнений экспертов существует несколько алгоритмов формирования оценок 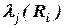 .
.
a) Косвенный метод с одним экспертом по рискам
Результатом опроса эксперта по рискам является набор матриц 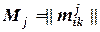 ,
, 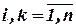 , где n - число потенциальных рисковых событий;
, где n - число потенциальных рисковых событий; 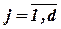 , где d - число независимых характеристик качества. Число
, где d - число независимых характеристик качества. Число 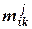 показывает, насколько, по мнению эксперта по рискам, степень влияния потенциального рискового события
показывает, насколько, по мнению эксперта по рискам, степень влияния потенциального рискового события  на характеристику качества
на характеристику качества 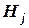 предпочтительней степени влияния последствий потенциального рискового события
предпочтительней степени влияния последствий потенциального рискового события 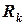 . Понятия, которыми оперирует эксперт, и интерпретация этих понятий значениями
. Понятия, которыми оперирует эксперт, и интерпретация этих понятий значениями 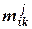 приведены в [4]. Вычисление значений
приведены в [4]. Вычисление значений 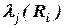 в этом случае производится следующим образом:
в этом случае производится следующим образом:
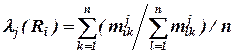 . (2.5)
. (2.5)
б) Косвенный подход с группой экспертов по рискам, характеризуемых весовыми коэффициентами значимости мнений
В случае привлечения группы экспертов по рискам, значимость мнений которых характеризуется весовыми коэффициентами, необходимо отдельно для каждого эксперта сформировать матрицу степеней влияния последствий рисков на характеристики качества проекта, а затем итоговое значение 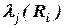 получить взвешенной аддитивной сверткой:
получить взвешенной аддитивной сверткой:
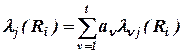 , (2.6)
, (2.6)
где t - число экспертов по рискам.
в) Косвенный подход с группой экспертов по рискам, характеризуемых нечетким отношением предпочтения мнений
При желании получить более объективное решение можно рассмотреть принцип формирования оценок 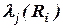 с группой экспертов по рискам, характеризуемых не весовыми коэффициентами, а с помощью нечеткого отношения предпочтения между ними. В этом случае вектор предпочтения мнений каждого из экспертов по рискам можно получить по следующей формуле:
с группой экспертов по рискам, характеризуемых не весовыми коэффициентами, а с помощью нечеткого отношения предпочтения между ними. В этом случае вектор предпочтения мнений каждого из экспертов по рискам можно получить по следующей формуле:
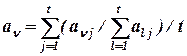 , (2.7)
, (2.7)
где 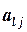 - значение, характеризующее, насколько предпочтительнее мнение l-го эксперта по рискам относительно мнения j-го эксперта.
- значение, характеризующее, насколько предпочтительнее мнение l-го эксперта по рискам относительно мнения j-го эксперта.
Далее по формуле (2.6) вычисляем значение 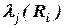 , принимая за
, принимая за 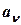 значения, получаемые по формуле (2.7).
значения, получаемые по формуле (2.7).
При использовании группы экспертов по рискам возникает проблема согласованности мнений экспертов, которая может решаться путем итерационной корректировки значимости мнений экспертов по рискам, алгоритмы которой рассмотрены А.С. Рыковым.
Получив по одной из формул (2.3) - (2.7) отдельные оценки влияния последствий Ri на характеристики качества проекта, представим совокупность этих оценок нечетким множеством:
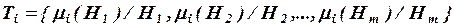 ,
,
где  .
.
Свертку вектора степеней влияния последствий потенциальных рисковых событий 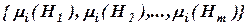 согласно [3] осуществляем, используя аддитивный критерий:
согласно [3] осуществляем, используя аддитивный критерий:
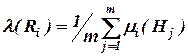 . (2.8)
. (2.8)
Если характеристики качества проекта Hj имеют различную степень важности, то общую задачу свертки вектора степеней влияния последствий рисков решаем, используя взвешенный аддитивный критерий:
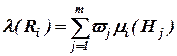 , (2.9)
, (2.9)
где vj - весовые коэффициенты соответствующих характеристик качества проекта, которые должны удовлетворять следующим ограничениям:
wj ³ 0, 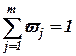 . (2.10)
. (2.10)
Решением поставленной задачи (2.1) является вектор W(R) степеней влияния последствий рисков на обобщенный критерий качества проекта такой, что W(Ri)=l(Ri).
Особенностями алгоритма D1 является то, что он работает только при независимых характеристиках качества проекта и при количественном способе задания оценок степени влияния последствий рисков на характеристики качества проекта, а также при независимых рисках.
2.2.2.2. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Рассмотрим пример решения задачи (2.1) с использованием исходных данных, полученных из реального программного проекта. Так, в ходе выполнения проекта по созданию системы документооборота предприятия при формировании «Начального руководства пользователя» были получены следующие проектные данные:
а) множество характеристик качества, заданное кортежем H ={H1, H2,H3}, где H1 - сопровождаемость, H2 - корректность, H3 – мобильность;
б) важность характеристик, заданная коэффициентами wj={0.6, 0.1, 0.3};
в) в результате идентификации рисков проекта выявлен список из четырех потенциальных рисковых событий R={R1, R2, R3, R4}, где R1 - отсутствие описания интерфейсов с пользователями; R2- отсутствие комментариев в точках входа и выхода программы; R3 - несоответствие комментариев принятым соглашениям; R4 - отсутствие описания алгоритмов;
г) экспертная информация относительно предпочтительности влияния последствий рисков на характеристики качества Hj согласно косвенному методу формализации экспертной информации для одного эксперта по рискам, представлена в виде набора матриц Mj:
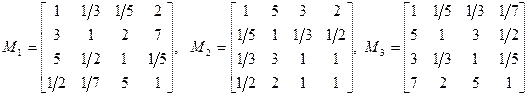 .
.
Используя приведенные исходные данные, решаем задачу определения вектора степеней влияния последствий рисков на обобщенный критерий качества проекта. В качестве метода решения задачи применим адекватный исходным данным алгоритм D1.
Шаг 1. Согласно формуле (2.5) из матриц M1-M3 определим степени влияния последствий Ri на характеристики качества Hj:
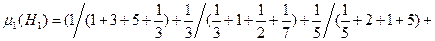
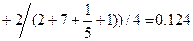 ;
;
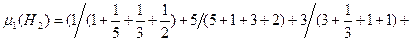
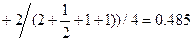 ;
;
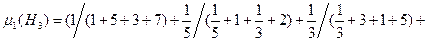
 .
.
Аналогично получим степени влияния последствий остальных трех рисков на характеристики качества Hj.
Шаг 2. Представим оценку влияния последствий потенциального рискового события Ri на характеристики качества проекта программного изделия нечетким множеством Ti, характеризующим степень влияния последствий Ri на характеристики качества проекта:
T1= {0,124/H1, 0,485/H2, 0,058/H3};
T2= {0,423/H1, 0,090/H2, 0,301/H3};
T3= {0,246/H1, 0,217/H2, 0,128/H3};
T4= {0,207/H1, 0,216/H2, 0,541/H3}.
Шаг 3. Вследствие того, что важность характеристик определяется коэффициентами wj={0.6, 0.1, 0.3}, сверку вектора степеней влияния последствий рисков произведем по формуле (2.9):
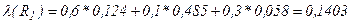 ;
;
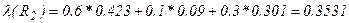 ;
;
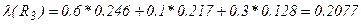 ;
;
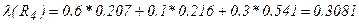 .
.
Шаг 4. В итоге получим вектор степеней влияния последствий потенциальных рисковых событий на обобщенный критерий качества проекта программного изделия 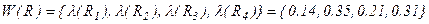 , необходимый далее для решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта программных изделий.
, необходимый далее для решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта программных изделий.
Достоинствами алгоритма D1 при решении задачи (2.1) являются:
· простота программной реализации;
· возможность учета оценки как одного, так и группы экспертов по рискам проекта;
· использование косвенного подхода к формированию оценки степени влияния последствий рисков, что позволяет снизить ошибки субъективного влияния на результаты определения оценки.
Недостатками алгоритма D1 являются:
· учет только количественного способа оценки степени влияния последствий рисков на Hj;
· работа данного подхода только при независимых характеристиках качества, что является частным случаем общей иерархической модели характеристик качества проекта;
· отсутствие учета возможной связности потенциальных рисковых событий по стадиям ЖЦ проекта.
2.2.3. РЕШЕНИЕ ЗАДАЧИ ПРИ НЕЗАВИСИМЫХ ХАРАКТЕРИСТИКАХ КАЧЕСТВА И ВЕРБАЛЬНОМ ЗАДАНИИ СТЕПЕНИ ВЛИЯНИЯ ПОСЛЕДСТВИЙ НЕЗАВИСИМЫХ РИСКОВ
2.2.3.1. ФОРМАЛИЗАЦИЯ ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ
Основным недостатком алгоритма D1 при решении задачи (2.1) является возможность использования лишь количественного способа задания экспертами по рискам степени влияния последствий рисков на характеристики качества проекта, а качественные оценки в виде вербальных высказываний на профессиональном языке не могут учитываться. Устранение этого недостатка возможно при использовании лингвистического подхода к решению поставленной задачи, что позволяет использовать при определении степени влияния последствий рисков субъективные оценки, выражаемые с помощью высказываний на профессиональном языке эксперта по рискам.
Данный подход основан на определении лингвистической переменной, сформулированном Л.Заде и развитый в последующих работах.
Определение 2.2. Лингвистической переменной (ЛП) называется кортеж
<b, T, U, G 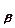 , M
, M 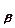 >, (2.11)
>, (2.11)
где b– наименование лингвистической переменной;
Т - терм-множество ЛП;
U - область определения элементов терм-множества;
G 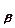 - синтаксическая процедура образования новых терм-множеств;
- синтаксическая процедура образования новых терм-множеств;
M 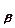 - семантическая процедура, позволяющая приписать каждому новому значению, образуемому процедурой G
- семантическая процедура, позволяющая приписать каждому новому значению, образуемому процедурой G 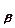 , некоторую семантику путем формирования соответствующего нечеткого множества.
, некоторую семантику путем формирования соответствующего нечеткого множества.
Например, необходимо оценить надежность конкретного проекта программного изделия. Надежность, измеряемая интенсивностью отказов (1/ч), задана в интервале [0.001, 0.01]. Формализация такого описания может быть произведена с помощью следующей лингвистической переменной:
<надежность, T, [0.001, 0.01], G 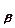 , M
, M 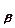 >,
>,
где Т = {низкая, средняя, высокая}; G 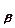 - процедура перебора элементов множества T; M
- процедура перебора элементов множества T; M 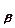 - процедура экспертного опроса.
- процедура экспертного опроса.
Для формализации многокритериальных задач, к числу которых принадлежит поставленная задача (2.1), удобно использовать структурированные лингвистические переменные [3].
Определение 2.3. Лингвистическая переменная называется структурированной, если ее терм-множество Т(Х) и функцию М 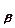 (Х), которая ставит в соответствие каждому элементу терм-множества его смысл, можно задать алгоритмически, а синтаксическое и семантическое правило, связанное со структурированной лингвистической переменной (СЛП), можно рассматривать как алгоритмические процедуры для порождения элементов множества Т(Х) и вычисления смысла каждого терма в Т(Х) соответственно.
(Х), которая ставит в соответствие каждому элементу терм-множества его смысл, можно задать алгоритмически, а синтаксическое и семантическое правило, связанное со структурированной лингвистической переменной (СЛП), можно рассматривать как алгоритмические процедуры для порождения элементов множества Т(Х) и вычисления смысла каждого терма в Т(Х) соответственно.
Основываясь на определениях 2.2 - 2.3, задача (2.1) может быть сформулирована следующим образом.
Пусть при планировании проекта выделены m несвязанных характеристик качества H={H1, H2, …, Hm}, на которые заданы ограничения в техническом задании. На этапе идентификации определен список из n потенциальных рисковых событий R={R1,R2,…,Rn}. Сформируем структурированную лингвистическую переменную с именем “Степень влияния последствий ПРС на обобщенный критерий качества проекта”. Элементы терм-множества лингвистических переменных, образующих СЛП, будут представлять собой вербальное описание степени влияния последствий рисков на отдельные характеристики качества проекта.
Оценим степени влияния последствий Ri на Hj путем экспертного выбора наиболее соответствующего элемента терм-множества j-й ЛП (соответственного вербального описания степени влияния последствий Riна характеристику качества Hj). Используя семантические правила, определяем численное значение вербального описания степени влияния последствий Ri на характеристики качества проекта 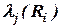 , которое представляет собой степень влияния последствий Riна Hj.
, которое представляет собой степень влияния последствий Riна Hj.
Используя положения теории нечетких множеств, представляем полученные результаты в виде совокупности нечетких множеств:
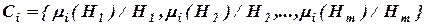 , (2.12)
, (2.12)
где 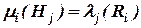 .
.
Вычислим далее значение степени влияния последствий риска на обобщенный критерий качества проекта, используя аддитивный критерий свертки:
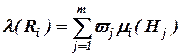 , (2.13)
, (2.13)
где wj - коэффициент важности j-й характеристики качества, который должен отвечать следующим условиям:
wj ³ 0, 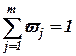 . (2.14)
. (2.14)
Решением поставленной задачи (2.1) является вектор W(R) степеней влияния последствий рисков на обобщенный критерий качества проекта такой, что W(Ri)=l(Ri).
Особенностями данного подхода является то, что он работает только при независимых характеристиках качества проекта, вербальном способе задания оценки степени влияния последствий влияния рисков на характеристики качества и при независимых рисках.
2.2.3.2. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Рассмотрим пример решения задачи (2.1) на основе реальных проектных данных. Так, в ходе разработки проекта системы документооборота предприятия при формировании «Начального руководства пользователя» в соответствии с постановкой задачи (2.1) были получены следующие проектные данные:
а) множество характеристик качества, заданных кортежем H ={H1, H2,H3}, где H1 - сопровождаемость, H2 - корректность, H3 – мобильность;
б) важность характеристик, заданная коэффициентами wj={0.6, 0.1, 0.3};
в) в результате идентификации рисков проекта выявлен список из четырех потенциальных рисковых событий R={R1, R2, R3, R4}, где R1 - отсутствие описания интерфейсов с пользователями; R2- отсутствие комментариев в точках входа и выхода программы; R3 - несоответствие комментариев принятым соглашениям; R4 - отсутствие описания алгоритмов.
Задав такие исходные данные, решим задачу определения вектора W(R) с помощью алгоритма D2на основе использования вербального способа задания оценки степени влияния последствий на характеристики качества проекта.
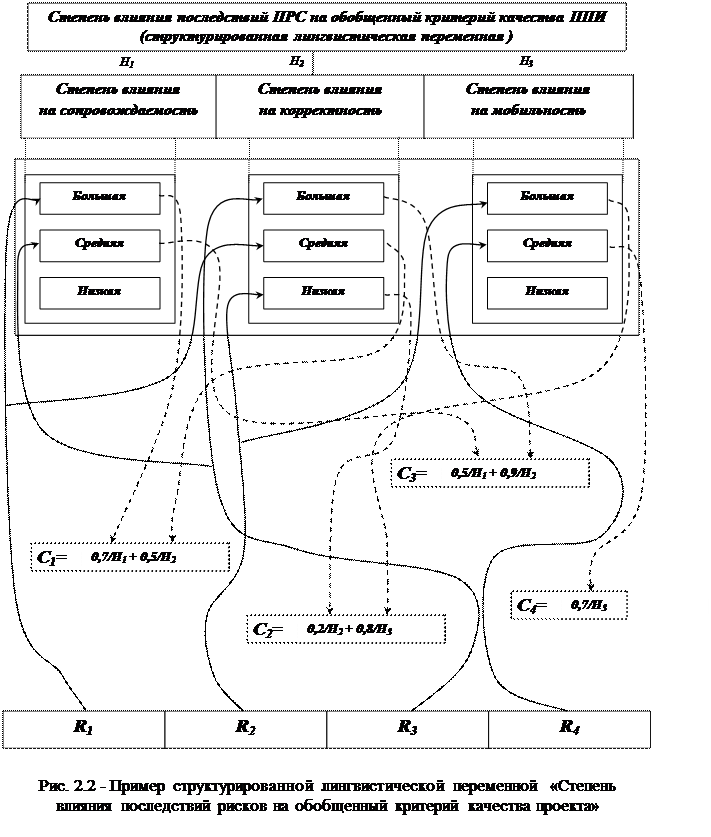
Шаг 1. Сформируем структурированную лингвистическую переменную с именем “Степень влияния последствий рисков на обобщенный критерий качества проекта”. Терм-множествами данной СЛП являются следующие лингвистические переменные с именами: “Степень влияния на сопровождаемость”, “Степень влияния на корректность”, “Степень влияния на мобильность”.
Шаг 2. Оценим степень влияния последствий Ri на Hj путем экспертного выбора наиболее соответствующего терма j-й ЛП (соответствующего вербального описания степени влияния последствий Ri на Hj). Схематическое изображение данного процесса представлено на рис. 2.2.
Шаг 3. Определим численные значения вербальных описаний степени влияния последствий Ri на характеристики качества проекта l(рис. 2.2) и представим данные в виде нечетких множеств:
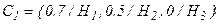 ;
;  ;
;
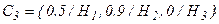 ;
; 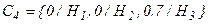 .
.
 |
Шаг 4. Согласно формуле (2.13) вычислим численное значение степени влияния потенциального рискового события Ri на характеристики качества:
 ;
;
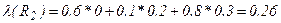 ;
;
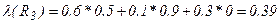 ;
;
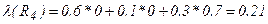 .
.
 |
Шаг 5. В итоге получим вектор степеней влияния последствий потенциальных рисковых событий на обобщенный критерий качества проекта программных изделий
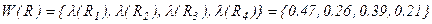 , необходимый для последующего решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта.
, необходимый для последующего решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта.
Достоинствами алгоритма D2при решении задачи (2.1) являются:
· простота программной реализации;
· использование вербального способа оценки степени влияния последствий рисков на характеристики качества проекта, что позволяет эксперту использовать высказывания профессионального языка.
Недостатками алгоритма D2 являются:
· подход работает на независимых характеристиках качества, которые являются частным случаем иерархической модели качества;
· отсутствует возможность учета связности потенциальных рисковых событий.
2.2.4. РЕШЕНИЕ ЗАДАЧИ ПРИ ИЕРАРХИЧЕСКОЙ МОДЕЛИ ХАРАКТЕРИСТИК КАЧЕСТВА И НЕЗАВИСИМЫХ РИСКАХ
2.2.4.1. ФОРМАЛИЗАЦИЯ ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ
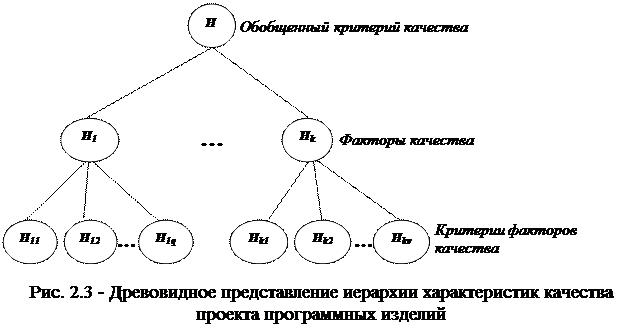
Основным ограничением двух предыдущих подходов (алгоритма D1 и D2) к решению задачи (2.1) является возможность учета только независимых характеристик качества проекта, что на практике является частным случаем иерархической модели качества проекта. Для устранения указанного ограничения в качестве модели характеристик качества проекта следует взять древовидную иерархическую структуру характеристик качества проекта, представленную на рисунке 2.3.
Первый уровень данной иерархии представлен обобщенным критерием качества проекта, значение которого показывает степень удовлетворения заданным требованиям к характеристикам качества программного проекта. На втором уровне иерархии выделяются факторы качества, характеризующие потребительски ориентированные свойства проекта (функциональные возможности, надежность, эффективность, практичность, сопровождаемость, мобильность).
На третьем уровне иерархии каждый фактор определяется своим набором критериев качества, характеризующим программно-ориентированные свойства (например, для фактора сопровождаемость указаны в [3] критерии: анализируемость, изменяемость, стабильность, тестируемость).
Выделим в данной иерархии элементы двух типов: элементы - “родители” и элементы - “потомки”. При этом элементы - “потомки” влияют на определение соответствующих элементов вышестоящего уровня иерархии, являющихся по отношению к первым элементами - “родителями”.
Пусть в ходе идентификации рисков определен набор из nпотенциальных рисковых событий R={R1,R2,…,Rn}.Иерархию характеристик качества представим элементами: вершиной обобщенного критерия качества H; вершинами факторов риска, заданных элементами вектора 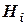 , и вершинами критериев для каждого фактора риска, представленных элементами матрицы
, и вершинами критериев для каждого фактора риска, представленных элементами матрицы 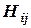 , где iÎ[1,k] – номер фактора риска; jÎ[1,vi] – номер критерия фактора i.
, где iÎ[1,k] – номер фактора риска; jÎ[1,vi] – номер критерия фактора i.
На первом шаге подготовительного этапа необходимо определить приоритет влияния элементов - “потомков” на соответствующие элементы - “родители”. Например, необходимо установить приоритеты влияния критериев качества анализируемость, изменяемость, стабильность, тестируемость на фактор качества - сопровождаемость. Для решения этой задачи будем использовать метод попарного сравнения. Данный метод основывается на построении матриц попарного сравнения, которые строятся для всех элементов - “потомков”, относящихся к соответствующему элементу - “родителю”. Парные сравнения проводятся в терминах доминирования одного элемента над другим. Полученные суждения, выраженные в целых числах с учетом девятибалльной шкалы, представлены в табл. 2.1.
Таблица 2.1 - Шкала степени значимости
| Степень значимости | Определение | Объяснение |
| Одинаковая степень влияния | Два элемента - “потомка” вносят одинаковый вклад в определение элемента - “родителя” | |
| Некоторое преобладание степени влияния одного элемента над другим (слабая значимость) | Существуют соображения в пользу предпочтительности влияния одного элемента - “потомка” перед другим на определение элемента - “родителя”, однако эти соображения недостаточно убедительны | |
| Существенное или сильное преобладание степени влияния одного элемента над другим | Имеются надежные данные или логические суждения для того, чтобы показать предпочтительность влияния одного из элементов - “потомков” | |
| Очевидное или очень сильное преобладание степени влияния одного элемента над другим | Убедительное свидетельство в пользу предпочтительности одного элемента - “потомка” перед другим | |
| Абсолютное преобладание степени влияния одного элемента над другим | Свидетельства в пользу предпочтительности одного элемента - “потомка” перед другим в высшей степени убедительны | |
| 2,4,6,8 | Промежуточное значение между двумя соседними значениями | Ситуация, когда необходимо компромиссное решение |
Заполнение квадратных матриц парных сравнений будем осуществлять по следующему правилу: если элемент M1 доминирует над элементом M2, то клетка, соответствующая строке M1 и столбцу M2, заполняется целым числом, а клетка, соответствующая строке M2 и столбцу M1, заполняется обратным к нему числом в противном случае клетка, соответствующая строке M2 и столбцу M1, заполняется целым числом, а клетка, соответствующая строке M1 и столбцу M2,заполняется обратным к нему числом. В случае равенства элементов M2и M1 в обе позиции ставятся единицы. В результате описанных выше действий, для данной иерархической структуры будет определен следующий набор матриц парных сравнений 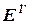 - степени влияния факторов качества на обобщенный критерий качества и
- степени влияния факторов качества на обобщенный критерий качества и 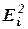 - степени влияния критериев качества на i-ый фактор качества.
- степени влияния критериев качества на i-ый фактор качества.
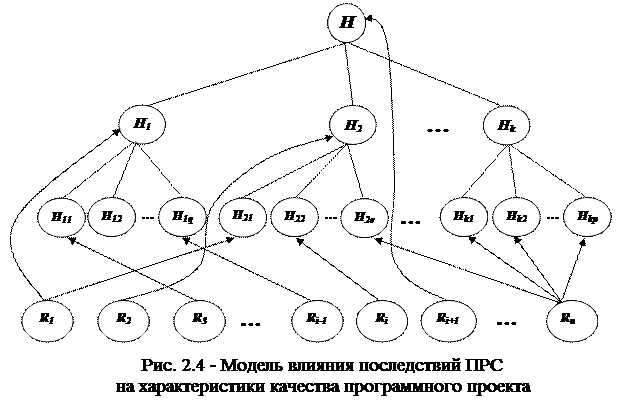
Следующим шагом подготовительного этапа является определение степени влияния последствий рисковых событий R на характеристики качества проекта. Далее рассмотрим случай, когда возможна оценка степени влияния последствий рисковых событий на все уровни иерархического дерева качества программного проекта (рис. 2.4).
Определение векторов приоритетов влияния последствий потенциальных рисковых событий на характеристики качества проекта может происходить одним из количественных способов [прямым для одного эксперта (2.3); прямым для группы экспертов (2.4); косвенным для одного эксперта (2.5); косвенным для группы экспертов, характеризующихся весовыми коэффициентами приоритетов значимости мнений каждого из них (2.6); косвенным методом для группы экспертов, характеризующихся вектором приоритетов значимости мнений каждого из них (2.7)], описанных в первом подходе к решению задачи (2.1) или вербальным способом (2.13), описанным во втором подходе к решению задачи (2.1).
Таким образом, в результате подготовительного этапа получается набор матриц:
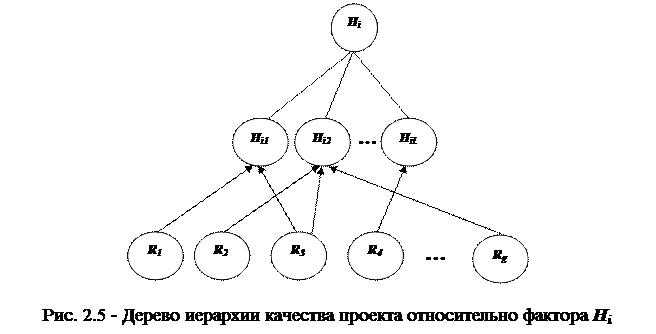 |
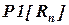 - вектор степеней влияния последствий рисковых событий на обобщенный критерий качества;
- вектор степеней влияния последствий рисковых событий на обобщенный критерий качества;
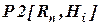 - матрица степеней влияния последствий рисковых событий на i-й фактор качества проекта;
- матрица степеней влияния последствий рисковых событий на i-й фактор качества проекта;
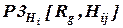 - набор матриц степеней влияния последствий рисковых событий на j-й критерий i-го фактора качества проекта.
- набор матриц степеней влияния последствий рисковых событий на j-й критерий i-го фактора качества проекта.
Задав все требуемые исходные данные, опишем решение задачи определения вектора W(R) на основе использования матрицы попарных сравнений Е и матрицы степеней влияния последствий рисков на характеристики качества H. Процедура решения данной задачи состоит из следующих шагов.
Шаг 1. Рассмотрим i–й фактор качества проекта 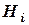 , являющийся элементом - “родителем”, и соответствующие элементы - “потомки”
, являющийся элементом - “родителем”, и соответствующие элементы - “потомки” 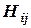 . Из списка потенциальных рисковых событий R выделим рисковые события, влияющие на критерии качества
. Из списка потенциальных рисковых событий R выделим рисковые события, влияющие на критерии качества 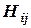 , и получим подмножество
, и получим подмножество 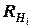 и соответственно матрицу:
и соответственно матрицу: 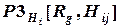 ,где g- количество потенциальных рисковых событий, влияющих на элементы - “потомки” фактора качества
,где g- количество потенциальных рисковых событий, влияющих на элементы - “потомки” фактора качества 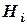 . В результате получим иерархическую структуру, показанную на рис. 2.5.
. В результате получим иерархическую структуру, показанную на рис. 2.5.
Шаг 2. На основе иерархической структуры, устанавливающей взаимосвязь между множеством потенциальных рисковых событий и набором критериев качества проекта ПИ, влияющим на i-й фактор качества (рис. 2.5), определим бинарную матрицу [Bi], которая содержит элементы bdj={0,1}, причем если последствие потенциального рискового события Rdвлияет на критерий качества 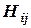 , то bdj=1, в противном случае bdj=0.
, то bdj=1, в противном случае bdj=0.
Шаг 3. На основе матрицы 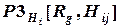 и определенной матрицы [Вi] построим матрицу [Аi]следующего вида:
и определенной матрицы [Вi] построим матрицу [Аi]следующего вида:
 . (2.15)
. (2.15)
В матрице [Аi] экспертные оценки 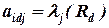 представляют оценки степени влияния последствий потенциальных рисковых событий на критерии качества
представляют оценки степени влияния последствий потенциальных рисковых событий на критерии качества 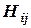 . Если Rd не влияет на критерий качества
. Если Rd не влияет на критерий качества 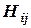 , то в матрице [А]соответствующее значение aidj=0.
, то в матрице [А]соответствующее значение aidj=0.
Шаг 4. В результате обработки матрицы попарных сравнений критериев качества 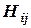 определим нормированный вектор приоритетов критериев
определим нормированный вектор приоритетов критериев 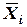 .
.
Шаг 5. Сформируем структурный критерий Li, отображаемый соответствующей диагональной матрицей [Li], представленной следующим образом:
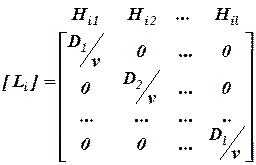 , (2.16)
, (2.16)
где 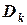 - число потенциальных рисковых событий R, последствия которых влияют на критерий качества
- число потенциальных рисковых событий R, последствия которых влияют на критерий качества 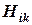 ;
;
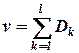 -общее количество связей по влиянию последствий рисков на характеристики качества проекта.
-общее количество связей по влиянию последствий рисков на характеристики качества проекта.
Шаг 6. Определим вектор приоритетов потенциальных рисковых событий Wi относительно фактора качества 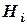 . Данная процедура реализуется перемножением следующих матриц и векторов:
. Данная процедура реализуется перемножением следующих матриц и векторов:
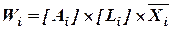 .(2.17)
.(2.17)
 |
В результате проведенных вычислений получим приоритеты потенциальных рисковых событий относительно фактора качества
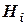 , заданные вектором Wi. Аналогичным способом вычислим приоритеты потенциальных рисковых событий относительно других факторов качества проекта.
, заданные вектором Wi. Аналогичным способом вычислим приоритеты потенциальных рисковых событий относительно других факторов качества проекта.
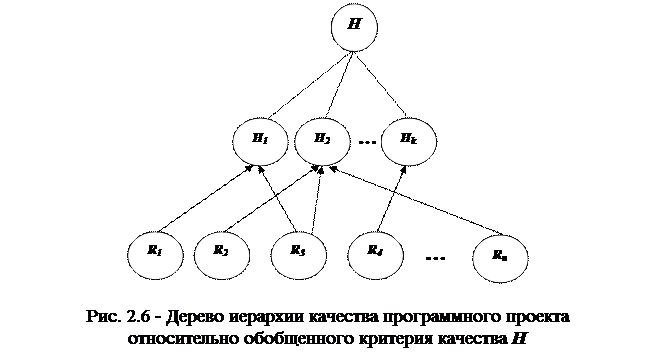
На следующем этапе данной процедуры рассмотрим дерево иерархии качества проекта. Здесь в качестве элемента - “родителя” выступает обобщенный критерий качества, а в качестве элементов - “потомков” факторы качества проекта ПИ (рис. 2.6).
На основе 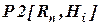 и множества Wiполучим матрицу
и множества Wiполучим матрицу 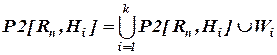 , представляющую собой степень влияния последствий рисковых событий на i-й фактор качества проекта. Далее на базе иерархической структуры, показанной на рис. 2.6, определим бинарную матрицу [B0], которая вычисляется аналогично матрице [Bi]. На следующем шаге на основе бинарной матрицы [B0] и матрицы
, представляющую собой степень влияния последствий рисковых событий на i-й фактор качества проекта. Далее на базе иерархической структуры, показанной на рис. 2.6, определим бинарную матрицу [B0], которая вычисляется аналогично матрице [Bi]. На следующем шаге на основе бинарной матрицы [B0] и матрицы 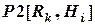 определим матрицу[A0],которая имеет следующий вид:
определим матрицу[A0],которая имеет следующий вид:
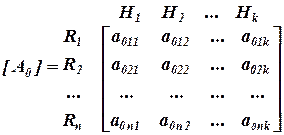 . (2.18)
. (2.18)
Далее аналогично шагам 4 и 5 определим нормированный вектор приоритетов факторов качества 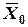 и структурный критерий L0, отображаемый диагональной матрицей [L0], имеющей такую же структуру, что и описанная выше диагональная матрица [Li] структурного критерия Li,. На следующем шаге определим вектор приоритетов влияния потенциальных рисковых событий относительно обобщенного критерия качества. Данная процедура реализуется перемножением следующих матриц и векторов:
и структурный критерий L0, отображаемый диагональной матрицей [L0], имеющей такую же структуру, что и описанная выше диагональная матрица [Li] структурного критерия Li,. На следующем шаге определим вектор приоритетов влияния потенциальных рисковых событий относительно обобщенного критерия качества. Данная процедура реализуется перемножением следующих матриц и векторов:
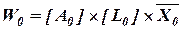 .(2.19)
.(2.19)
В итоге получим вектор 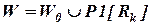 =
= 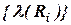 , представляющий собой вектор приоритетов влияния потенциальных рисковых событий на обобщенный критерий качества проекта, который необходим для последующего решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта программных изделий.
, представляющий собой вектор приоритетов влияния потенциальных рисковых событий на обобщенный критерий качества проекта, который необходим для последующего решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта программных изделий.
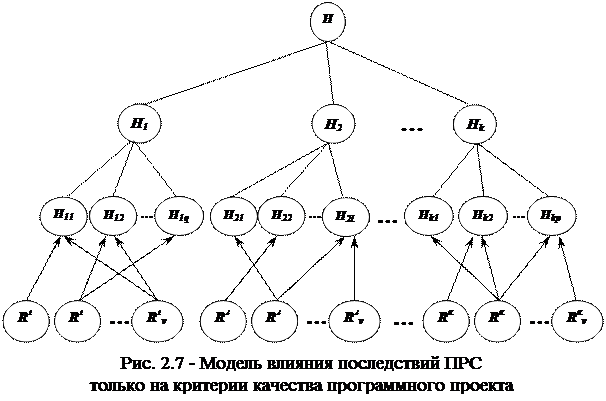
Для случая, когда имеется возможность выявить информацию о приоритетах влияния потенциальных рисковых событий только на критерии качества, находящиеся на самом низком уровне иерархии качества проекта, можно описать упрощенную процедуру определения вектора степеней влияния последствий рисков на обобщенный критерий качества. Данную ситуацию можно представить в виде следующей иерархии (рис. 2.7).
Для реализации такого алгоритма необходимо потенциальные рисковые события, последствия которых влияют на критерии качества, соответствующие нескольким различным факторам качества, продублировать в подгруппы потенциальных рисковых событий, относящихся к этим факторам качества.
Далее опишем процедуру получения вектора приоритетов влияния потенциальных рисковых событий на обобщенный критерий качества проекта.
Шаг 1. Вычислим векторы приоритетов потенциальных рисковых событий относительно критериев качества, используя 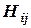 :
:
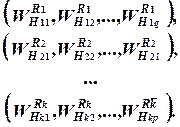 (2.20)
(2.20)
Шаг 2. Построимkматриц [Ai], у которых наименованиями строк являются варианты потенциальных рисковых событий, а наименованиями столбцов - критерии качества 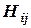 . Если вариант потенциального рискового события Rdне связан с критерием
. Если вариант потенциального рискового события Rdне связан с критерием 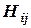 , то в матрице [Ai] на пересечении соответствующих строк и столбцов проставляется ноль.
, то в матрице [Ai] на пересечении соответствующих строк и столбцов проставляется ноль.
Шаг 3. Вычислим kвекторов приоритетов 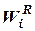 относительно факторов качества
относительно факторов качества 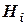 по выражениям:
по выражениям:
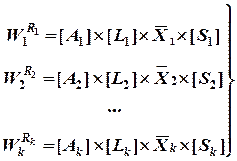 , (2.21)
, (2.21)
где [Li]– структурная матрица для изменения веса вариантов потенциальных рисковых событий пропорционально отношению Dz2/g1(Dz2– число потенциальных рисковых событий Ri1, последствия которых влияют на критерий качества 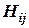 );
);
[ 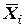 ] – вектор приоритетов критериев качества Hijотносительно фактора качества
] – вектор приоритетов критериев качества Hijотносительно фактора качества 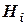 ;
;
[Si] – коэффициент нормирования вектора 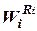 .
.
Шаг 4. Вычислим вектор приоритетов критериев 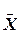 относительно обобщенного критерия качества иерархии Н.
относительно обобщенного критерия качества иерархии Н.
Шаг 5. Построим результирующую матрицу [A0], у которой наименованиями строк являются все рассматриваемые потенциальные рисковые события, а наименованиями столбцов - факторы качества 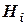 .
.
Шаг 6. Определим результирующий нормированный вектор приоритетов 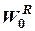 всех рассматриваемых рисков относительно обобщенного критерия качества Н на основании известного выражения:
всех рассматриваемых рисков относительно обобщенного критерия качества Н на основании известного выражения:
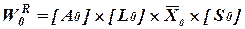 . (2.22)
. (2.22)
Этот вектор, аналогично первому случаю, необходим для решения задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества проекта программных изделий и за W(Ri) принимается значение 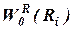 .
.
Особенностями и достоинствами рассмотренного алгоритма D3 является то, что он работает на общей произвольной иерархической модели характеристик качества проекта и как при количественном, так и при вербальном способе задания оценки степени влияния последствий рисков на характеристики качества и на независимых рисках.
2.2.4.2. ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
Рассмотрим пример решения задачи (2.1) на основе реальных проектных данных. Пусть в ходе разработки проекта по созданию системы документооборота предприятия и при формировании «Начальной технической архитектуры» в соответствии с постановкой задачи (2.1) были получены следующие проектные данные:
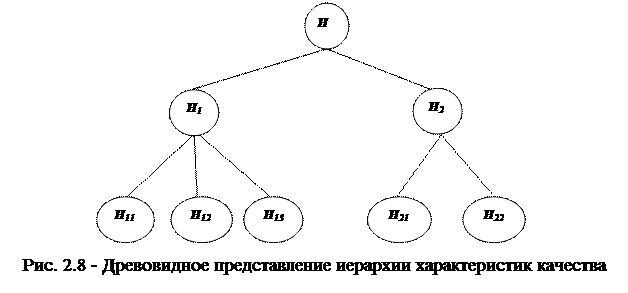
а) множество заданных характеристик качества, представленных иерархическим деревом (рис. 2.8), где введены следующие обозначения:
H - обобщенный критерий качества программного проекта;
H1 - надежность;
H11 - завершенность;
H12 - восстанавливаемость;
H13 -доступность;
H2 - сопровождаемость;
H21 -изменяемость;
H22 –тестируемость;
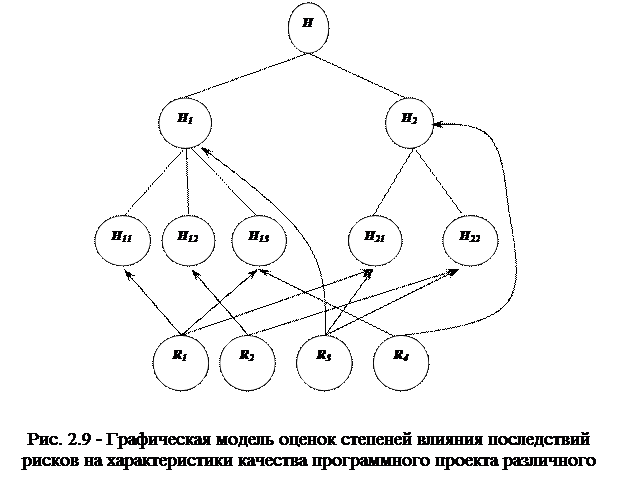
б) в ходе идентификации рисков выявлен список из четырех потенциальных рисковых событий R={R1, R2, R3, R4}, где R1 - невозможность обработки ошибочных ситуаций; R2 - отсутствие средств контроля непротиворечивости входных данных; R3 - отсутствие модульной схемы программы; R4 - отсутствие средств, обеспечивающих завершение процесса решения в случае помех;
в) экспертным способом заданы оценки степени влияния последствий рисков на характеристики качества проекта, графическое отображение которых показано на рис. 2.9.
 |
Графическую модель степеней влияния последствий рисков и модель предпочтений характеристик качества представим совокупностью векторов оценок:
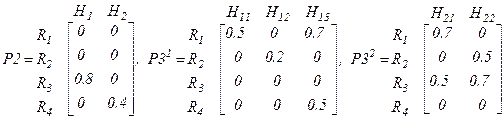 ,
,
и матриц предпочтений характеристик качества:
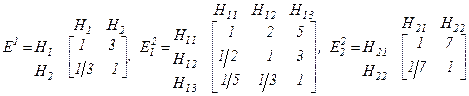 .
.
Рассмотрим принцип действия алгоритма D3на примере вышеописанных проектных данных.
Шаг 1. Выделим потенциальные рисковые события, влияющие на критерии фактора качества ПИ надежность (рис. 2.10).
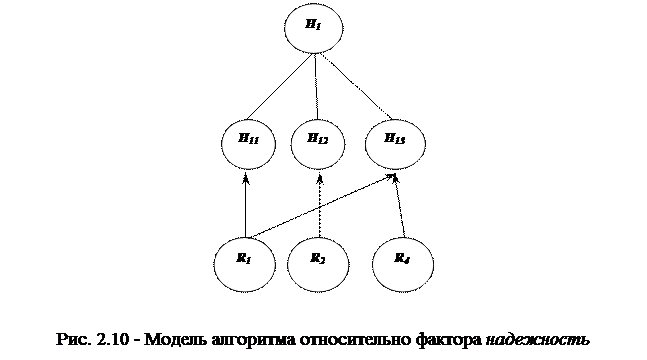
Шаг 2. На основе матрицы 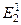 , используя принцип определения приоритетов критериев характеристики качества надежность на характеристику качества надежность (2.5) определим требуемый вектор приоритетов X1 элементов иерархии:
, используя принцип определения приоритетов критериев характеристики качества надежность на характеристику качества надежность (2.5) определим требуемый вектор приоритетов X1 элементов иерархии:
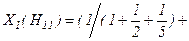
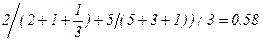 .
.
Аналогичным образом определим остальные элементы вектора приоритетов: 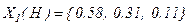 .
.
Шаг 3. На основе иерархической структуры определим бинарную матрицу 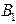 :
:
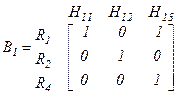 .
.
Шаг 4. На основе матрицы 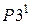 и определенной матрицы
и определенной матрицы 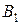 определим матрицу
определим матрицу 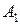 :
:
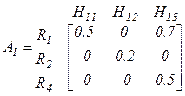 .
.
Шаг 5. Сформируем структурный критерий 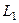 , отображаемый соответствующей диагональной матрицей
, отображаемый соответствующей диагональной матрицей 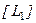 :
:
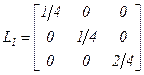 .
.
Шаг 6. Определим вектор приоритетов ПРС W1 относительно фактора качества надежность. Данная процедура реализуется перемножением следующих матриц и векторов:
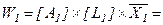
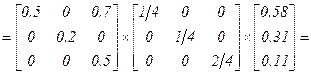
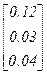 .
.
Аналогично шагам 1-6 определим вектор приоритетов 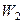 относительно фактора качества сопровождаемость. В итоге получим вектор приоритетов
относительно фактора качества сопровождаемость. В итоге получим вектор приоритетов
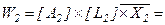
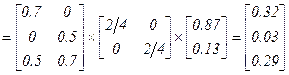 .
.
Шаг 7. Согласно алгоритму D3 далее необходимо перейти на следующий уровень иерархии и рассматривать предложенный алгоритм относительно обобщенного критерия качества, представленного на рис. 2.11.
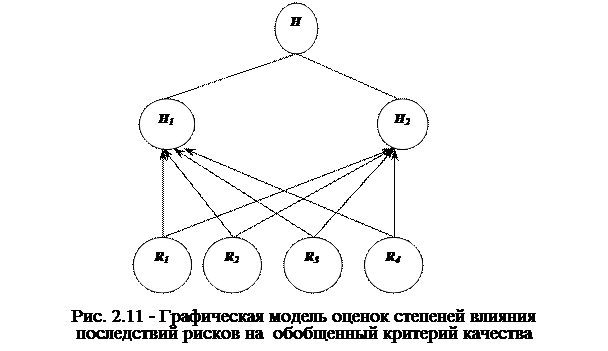 |
Особенностью данного перехода по алгоритму D3 является объединение полученных векторов приоритетов:
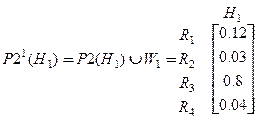 ,
,
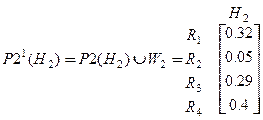 .
.
Шаг 8. Определим вектор приоритетов влияния факторов качества надежность и сопровождаемость на обобщенный критерий качества проекта:
 .
.
Шаг 9. Аналогично шагам 1-6 определим вектор приоритетов  относительно обобщенного критерия качества. В итоге получим вектор приоритетов:
относительно обобщенного критерия качества. В итоге получим вектор приоритетов:
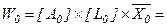

 .
.
Шаг 10. Таким образом, в итоге мы получили вектор степеней влияния последствий рисков на обобщенный критерий качества проекта  , необходимый для решения второй задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества.
, необходимый для решения второй задачи (2.36) выбора квазиоптимального состава контролируемых рисков качества.
Достоинствами алгоритма D3при решении задачи (2.1) являются:
· поддержка как вербального, так и количественного способа оценки степени влияния последствий рисков на характеристики качества проекта, что позволяет эксперту по рискам использовать высказывания профессионального языка;
· использование иерархической модели качества проекта программных изделий.
Недостатками (узкими местами) алгоритма D3являются:
· сложность программной реализации;
· отсутствие учета возможной связности потенциальных рисковых событий проекта.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какие основные этапы и процессы содержит процесс «Управление рисками проекта»?
2. Укажите назначение и содержание основных задач этапа анализа рисков проекта.
3. Дайте сравнительную характеристику алгоритмам определения вектора последствий рисков.
4. Раскройте постановку и способы решения задачи выбора квазиоптимальной совокупности контролируемых рисков качества.
5. Проанализируйте теоретические основы построения алгоритмов D1-D5 на практических примерах.
| <== предыдущая страница | | | следующая страница ==> |
| II. Тип организации верховной власти в государстве (форма государственного правления) | | | Роль службы экстренной медицинской помощи в чрезвычайных ситуациях |
Дата добавления: 2014-08-09; просмотров: 723; Нарушение авторских прав

Мы поможем в написании ваших работ!