
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уравнивание геодезического четырехугольника коррелатным способом
Для определения координат пунктов В и Д в геодезическом четырехугольнике (рис. 2) измерено равноточно (рi = 1) восемь углов между сторонами и диагоналями. Результаты измерений помещены в табл. 5.
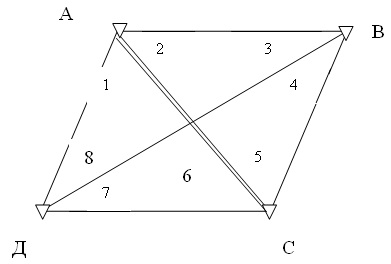
Рис. 2. Геодезический четырехугольник
Таблица 5
Результаты измерений
| № углов | Измеренные углы βi | № углов | Измеренные углы βi |
| 77°35′ 46,3″ | 36°00′ 05,7″ | ||
| 57° 00′ 57,0″ | 46° 29′ 49,3″ | ||
| 27° 22′ 57,6″ | 37° 54′ 10,8″ | ||
| 59° 35′ 57,7″ | 18° 00′ 15,7″ |
Определим число независимых условных уравнений.
Число необходимых измерений в линейно-угловой сети равно удвоенному числу вновь определяемых пунктов, t = 2 · 2 = 4. Число избыточных измерений
r = n - t = 8 - 4 = 4.
В геодезическом четырехугольнике имеют место четыре независимых условных уравнения, 3 - условных уравнения фигур и 1 - полюсное.
Составим условные уравнения связи.
Условное уравнение фигур: сумма углов плоского треугольника после уравнивания минус 180° равна нулю.
Обозначим βi = i. Для трех треугольников, например, ΔАВС, ΔАДС, ΔАВД условные уравнения фигур будут иметь вид:
1. 5 + ν5 + 2 + ν2 + 3 + ν3 + 4 + ν4 - 180° = 0;
2. 8 + ν8 + 1 + ν1 + 6 + ν6 + 7 + ν7 - 180° = 0;
3. 1 + ν1 + 2 + ν2 + 3 + ν3 + 8 + ν8 - 180° = 0.
Полюсное условное уравнение: отношение сторон, сходящихся в одной точке (полюсе), после уравнивания равно единице. Если полюс - точка А, то
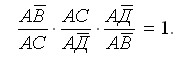
По теореме синусов, отношение сторон заменяют отношением синусов противолежащих углов:
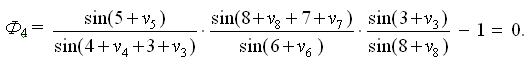
Составим условные уравнения поправок.
Условные уравнения фигур имеют линейный вид. Для перехода к условным уравнениям поправок следует вычислить невязки, которые равны суммам измеренных углов в треугольнике минус 180°.
1) ν5 + ν2 + ν3 + ν4 + w1 = 0; w1 = 5 + 2 + 3 + 4 - 180°= -2,0″;
2) ν8 + ν1 + ν6 + ν7 + w2 = 0; w2 = 8 + 1 + 6 + 7 - 180°= +2,1″;
3) ν1 + ν2 + ν3 + ν8 + w3 = 0; w3 = 1 + 2 + 3 +8 - 180°= -3,4″.
Полюсное условное уравнение связи приводят к линейному виду разложением в ряд Тейлора
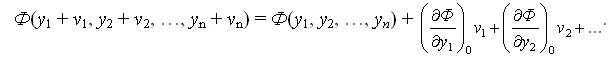 .
.
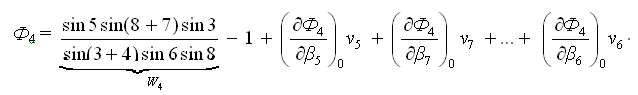 .
.
Частная производная функции Ф4 по аргументу β5 (углу числителя):
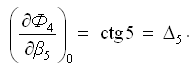
Частная производная функции Ф4 по аргументу β6 (углу знаменателя):
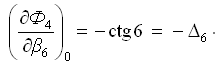
Частная производная функции Ф4 по аргументу β8 (углу числителя и знаменателя):
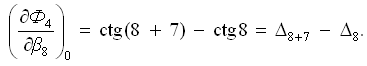
С учетом размерности поправок и невязки полюсное условное уравнение поправок имеет вид:
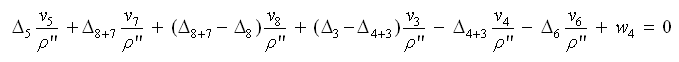
Умножив на ρ″, получим
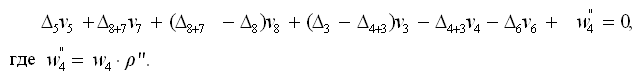
Определение коэффициентов Δi и невязки w″4 полюсного условного уравнения выполним на ПК по программе Polus.exe. Исходной информацией к программе являются углы числителя и знаменателя полюсного условного уравнения (табл. 6).
Таблица 6
Вычисление Δi и w″4
| ... | Числитель | ... | ... | Знаменатель | ... |
| № углов | βi | Δi | № углов | βi | Δi |
| 36°00′ 05,7″ | 1,38 | 3+4 | 86°58′ 55,3″ | 0,05 | |
| 8+7 | 55° 54′ 26, 5″ | 0,68 | 46° 29′ 49,3″ | 0,95 | |
| 27° 22′ 57,6″ | 1,93 | 18° 00′ 15,7″ | 3,08 |
w″4 = +2,67″.
Полюсное условное уравнение поправок принимает вид:
4) 1,38 ν5 + 0,68 ν7 + 1,88 ν3 - 0,05 ν4 - 0,95 ν6 - 2,40 ν8 + 2,67 = 0.
Составим весовую функцию.
Пусть
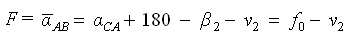
- дирекционный угол стороны АВ, вычисленный по результатам уравнивания.
Итак, получена следующая система условных уравнений поправок:
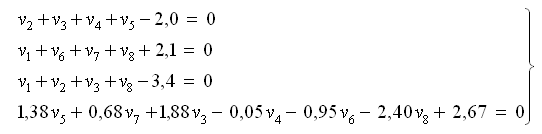 (24)
(24)
Таблица 7
Коэффициенты условных уравнений и функции
| № измерения | a | b | c | d | f | ν |
| ... | ||||||
| -1 | ... | |||||
| +1.88 | ... | |||||
| -0.05 | ... | |||||
| +1.38 | ... | |||||
| -0.95 | ... | |||||
| +0.68 | ... | |||||
| -2.40 | ... |
и весовая функция:
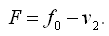
Коэффициенты условных уравнений и функции поместим в табл. 7.
Дальнейшее решение задачи выполните на ПК по программе KORREL.EXE. Таблицу коэффициентов условных уравнений вводите по столбцам.
Выпишите с экрана:
1. Значения поправок к результатам измерений в столбец ν табл. 7.
2. Среднюю квадратическую ошибку измерения - m.
3. Обратный вес 1/PF и среднюю квадратическую ошибку функции - mF.
Вычислите уравненные значения углов 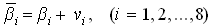 и сделайте контроль уравнивания.
и сделайте контроль уравнивания.
| <== предыдущая страница | | | следующая страница ==> |
| Уравнивание нивелирной сети коррелатным способом | | | Параметрические уравнения |
Дата добавления: 2014-09-08; просмотров: 1068; Нарушение авторских прав

Мы поможем в написании ваших работ!