
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выравнивание ряда
|
Читайте также: |
Вариант 28
Задача № 1.
Произведите группировку магазинов по признаку размер торговой площади (см. таблицу задачи №1 варианта XXIX), образовав при этом, пять групп с равными интервалами. Рассчитайте по каждой группе издержки обращения и численность продавцов. Результаты группировки представьте в табличной форме и сформулируйте выводы.
| № магазина | Издержки обращения (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) |
| 20,2 | |||
| 40,0 | |||
| 22,4 | |||
| 29,1 | |||
| 20,6 | |||
| 28,4 | |||
| 10,9 | |||
| 38,7 | |||
| 11,7 | |||
| 40,2 | |||
| 23,6 | |||
| 21,6 | |||
| 9,2 | |||
| 26,2 | |||
| 22,3 |
Расставим исходные данные (Табл.1) в порядке возрастания издержек обращения. В результате получим Таблицу 2.
| Таблица 2 | |||
| № магазина | Издержки обращения (млн. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) |
| 9,2 | |||
| 23,6 | |||
| 22,3 | |||
| 21,6 | |||
| 20,2 | |||
| 10,9 | |||
| 38,7 | |||
| 22,4 | |||
| 26,2 | |||
| 20,6 | |||
| 11,7 | |||
| 28,4 | |||
| 40,2 | |||
| 29,1 | |||
Ширина интервала группировки
h=(xmax – xmin)/5 = (1840 –- 980)/5=172 м2..
В результате получим группы в интервалах:
| Группы: | Верхняя граница | Нижняя граница | Число магазинов |
| 1 группа | |||
| 2 группа | |||
| 3 группа | |||
| 4 группа | |||
| 5 группа |
Для каждой группы рассчитаем размер торговой площади и численность продавцов. Результаты расчетов запишем в таблицу:
| Таблица 3 | |||
| Торговая площадь (м2) | Число магазинов | Издержки группы (млн. руб.) | Численность продавцов (чел.) |
| 980–1152 | 32,8 | ||
| 1152–1324 | 22,3 | ||
| 1324–1496 | |||
| 1496–1668 | 32,3 | ||
| 1668–1840 | 137,7 |
Выводы:
1. Магазины по торговой площади распределены неравномерно.
2. Численность продавцов и издержки обращения в группе зависят от размера группы.
Задача 2
Исходные данные
| Торговая площадь (м2) | Число магазинов |
| 980–1152 | |
| 1152–1324 | |
| 1324–1496 | |
| 1496–1668 | |
| 1668–1840 |
Для вычисления статистических характеристик исходного интервального ряда необходимо выбрать некоторое среднее значения xi для каждого i-го интервала. Обычно это середина ряда. Поэтому получаем следующую таблицу:
| Торговая площадь (м2), xi | Число магазинов в группе, ni |
Тогда средние издержки: 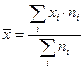 ; Дисперсия:
; Дисперсия:  ;
;
Среднее квадратическое отклонение: 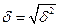 Коэффициент вариации:
Коэффициент вариации: 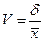
Для расчета составим таблицу (последний столбец таблицы: накопленная частота группы):
| Торговая площадь группы (м2), xi | Число магазинов в группе, ni | xi·ni | ni·(xi-xср)2 | 
|
| 322136,9 | 13,3% | |||
| 52593,8 | 20,0% | |||
| 19722,7 | 60,0% | |||
| 26296,9 | 73,3% | |||
| 328711,1 | 100,0% | |||
| всего: | 749461,3 |
средняя торговая площадь: 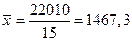 м2; Дисперсия:
м2; Дисперсия: 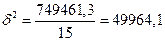 ;
;
Среднее квадратическое отклонение: 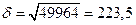 м2
м2
Коэффициент вариации: 
Мода
Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой. В нашем случае это третий интервал с частотой (6).
Модальное значение: 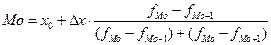
где x0 — нижняя граница модального интервала (x0 = 1324) ;
fМо — частота в модальном интервале (6);
fМо–1 — частота в предыдущем интервале (1);
fМо+1 — частота в следующем интервале за модальным (2);
Dx — величина интервала (172)
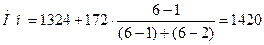 м2
м2
Мода равна 1420 м2
.
Медиана
Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. В нашем случае это третий интервал: [1324–1496] (накопленная частота превышает 50%)
Медианное значение:
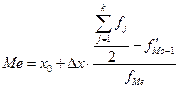
где x0 — нижняя граница медианного интервала (x0 =1324);
f’Мe-1 — накопленная частота в интервале, предшествующем медианному; (f’Мe-1 =2+1=3);
fМе — частота в медианном интервале (fМе = 6);
k — число групп;
Dx — величина интервала (172)
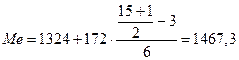 м2
м2
Медиана равна 1467 м2
Вариант XXVIII
Задача № 1.
Для оценки стоимости основных средств региона была проведена 5 %-ная механическая выборка, в результате чего установлено:
| Группы предприятий по стоимости основных средств, тыс. руб. | Число предприятий |
| До 100 | |
| 100 – 200 | |
| 200 – 300 | |
| 300- 400 | |
| 400 - 500 | |
| 500 и более |
Определите:
1) по включенным в выборку предприятиям:
а) среднюю стоимость основных средств на одно предприятие;
б) долю предприятий со стоимостью основных средств более 500 тыс. руб.;
2) с вероятностью 0,988 пределы, в которых можно ожидать среднюю стоимость основных средств на одно предприятие и долю предприятий со стоимостью основных средств более 500 тыс. руб. в целом по региону.
Решение:
Для вычисления статистических характеристик исходного интервального ряда необходимо выбрать некоторое среднее значения xi для каждого i-го интервала. Обычно это середина ряда. Поэтому получаем следующую таблицу:
| Стоимость ОФ, xi | Число предприятий, ni |
| Итого: |
1. Тогда средняя стоимость ОФ: 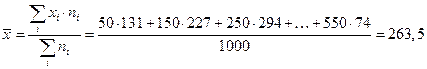 тыс. руб
тыс. руб
Дисперсия 
2. Доля предприятий со стоимостью основных средств более 500 тыс. руб по выборке: 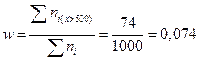
3. Интервал для математического ожидания: 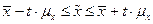
При бесповторной выборке средняя ошибка выборки μx определяется по формуле:
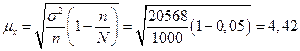
Для вероятности 0,988 коэффициент t=2,5, поэтому
 тыс. руб.
тыс. руб.
Т.о., с вероятностью 0,988 средняя стоимость ОФ с лежит в интервале [252,45–274,55] тыс. руб.
Интервал для оценки доли предприятий со стоимостью основных средств более 500 тыс. руб по выборке:
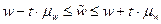
w = 0,074
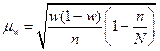 . У нас 5%-ная выборка, т.е.
. У нас 5%-ная выборка, т.е. 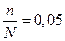 ,
, 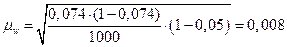
Для вероятности 0,988 коэффициент t=2,5, поэтому
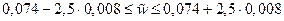

т.е. с вероятностью 0,988 доля предприятий со стоимостью основных средств более 500 тыс. руб. лежит в интервале [0,074-0,094]
Задача № 2.
Имеется информация о числе студентов дневной формы обучения в высших учебных заведениях города, тыс. чел.
| Год | Итого | ||||||
| Число студентов, тыс. чел | 13,5 | 13,46 | 13,6 | 13,9 | 15,3 | 82,76 |
Для анализа динамики численности студентов вузов исчислите: 1) среднегодовое число студентов; 2) базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста и темпов прироста числа студентов; 3) проверьте ряд динамики числа студентов на наличие тренда. Используя метод аналитического выравнивания, постройте уравнение линии выравнивания; 4) изобразите динамику числа студентов на графике. Сделайте выводы и прогноз на 2013 г.
Решение:
Найдем показатели динамики:
Абсолютный базисный прирост: ∆бi=xi–x0
Абсолютный цепной прирост: ∆цi=xi–xi-1
Темп роста базисный: 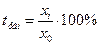 Темп роста цепной:
Темп роста цепной: 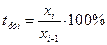
Темп прироста базисный: 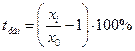 Темп прироста цепной:
Темп прироста цепной: 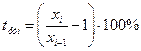
Среднее значение ряда: 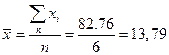 (тыс.чел.)
(тыс.чел.)
Средний темп роста: 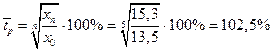
Средний темп прироста: 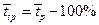 =2,5%
=2,5%
Средний абсолютный прирост: 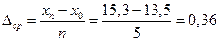 тыс.чел.
тыс.чел.
Расчеты показателей динамики занесем в таблицу:
За базисное принимаем значение 2004 года: x0 = 13,5.
| Год | ||||||
| Число студентов | 13,5 | 13,46 | 13,6 | 13,9 | 15,3 | |
| абсолютный прирост базисный | -0,5 | -0,04 | 0,1 | 0,4 | 1,8 | |
| абсолютный прирост цепной | -0,5 | 0,46 | 0,14 | 0,3 | 1,4 | |
| темп роста базисный | 96,3% | 99,7% | 100,7% | 103,0% | 113,3% | |
| темп роста цепной | 96,3% | 103,5% | 101,0% | 102,2% | 110,1% | |
| темп прироста базисный | -3,7% | -0,3% | 0,7% | 3,0% | 13,3% | |
| темп прироста цепной | -3,7% | 3,5% | 1,0% | 2,2% | 10,1% |
Тренд
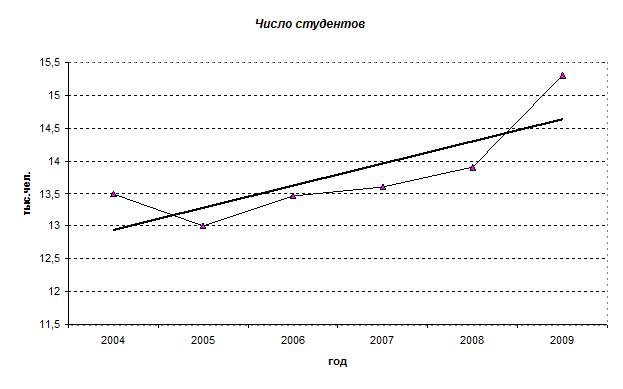
Построим график изменения числа студентов по годам (Рис. 1)
По графику видно, что существует очевидный тренд, близкий к линейному.:
Выравнивание ряда
Для выравнивания ряда примем обозначение дат с нулем в середине, т.е. t*2007=–1, t*2008=1. Тогда коэффициенты параметров линейного тренда находятся из уравнений:
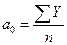
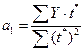
Составим таблицу:
| Год | t | Y | t2 | t*Y |
| -5 | 13,5 | -67,5 | ||
| -3 | -39 | |||
| -1 | 13,46 | -13,46 | ||
| 13,6 | 13,6 | |||
| 13,9 | 41,7 | |||
| 15,3 | 76,5 | |||
| Сумма: | 82,76 | 11,84 |
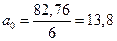
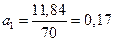
Уравнение выровненного ряда: Y=13,8 + 0,17·t
Уравнение выровненного ряда дано на Рис.1 утолщённой линией.
По этому уравнению можно спрогнозировать число студентов на 2013 год (t=13)
Yt=13=13,8 + 0,17·13 = 16 тыс.чел.
По исходным данным построен график динамики числа студентов и выровненный ряд.
Выводы:
1. Показатели динамики характеризуют одним показателем общий характер развития исследуемого процесса во времени.
2. Наглядным и удобным представлением развития процесса являются статистические графики.
Вариант XXVIII
Задача № 1. Себестоимость и объем продукции предприятия характеризуются следующими данными:
| Изделие | Себестоимость единицы изделия, руб. | Выработано продукции, тыс. шт. | ||
| Январь, z0 | Февраль, z1 | Январь, q0 | Февраль, q1 | |
Определите: 1) общий индекс затрат на все изделия; 2) общий индекс себестоимости единицы изделия; 3) общий индекс физического объема продукции. Сделайте выводы и покажите взаимосвязь индексов.
Решение:
1. общий индекс затрат на все изделия: 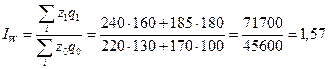
общий индекс себестоимости единицы изделия: 
общий индекс физического объема продукции: 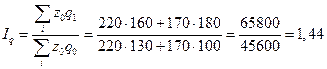
Связь индексов: 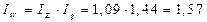
Вывод:
Таким образом, рост затрат на все изделия на 57% в основном связан с ростом физического объема продукции (на 44%).
Задача № 2. Имеются данные о численности работников и их заработной плате в вузах региона.
| Специализация работников | Численность работников, чел. | Заработная плата, руб. | ||
| базисный период, q0 | отчетный период, q1 | базисный период, p0 | отчетный период, p1 | |
| Технические | ||||
| Экономические |
Определите: 1) среднюю заработную плату в целом за два периода; 2) изменение средней заработной платы: а) за счет изменения структуры работников; б) изменения заработной платы отдельных категорий работников. Покажите связь между исчисленными индексами. Сделайте выводы.
Решение:
- Средняя заработная плата:
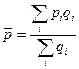
. Средняя заработная плата базисного периода: 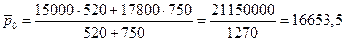 руб.
руб.
. Средняя заработная плата отчётного периода:  руб.
руб.
средняя заработная плата в целом за два периода
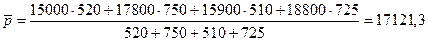 руб.
руб.
Индекс заработной платы: 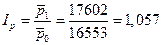
2) изменение средней заработной платы:
1. а) за счет изменения структуры работников: Индекс структурных сдвигов:
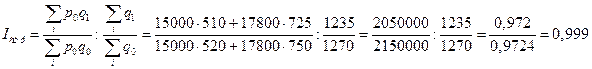
б) изменения заработной платы отдельных категорий работников: 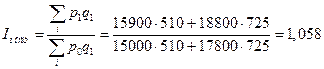
Вывод:
Таким образом, весь прирост средней заработной платы связан с ростом заработной платы каждой группы работников в отчётном периоде.
| <== предыдущая страница | | | следующая страница ==> |
| КОНТРОЛЬНАЯ РАБОТА №3 (по теме №5) | | | РАБОЧАЯ ПРОГРАММА. Учебно-методический комплекс |
Дата добавления: 2014-09-08; просмотров: 396; Нарушение авторских прав

Мы поможем в написании ваших работ!