
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ МЕТОДОМ ОТРЫВА КАПЕЛЬ
ЦЕЛЬ РАБОТЫ: изучение поверхностных явлений в жидкости и определение коэффициента поверхностного натяжения методом отрыва капель.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: бюретка, два химических стакана, штатив, весы с разновесами, исследуемая жидкость.
1. Краткие теоретические сведения:
Жидкости, как газы и твердые тела, состоят из мельчайших частиц – молекул, между которыми действуют силы взаимного притяжения и отталкивания. Силы молекулярного взаимодействия быстро убывают с увеличением расстояния от молекулы и уже на расстоянии R, равном 10-7см, практически не проявляются (радиус самих молекул r = 0,5*10-7см).
Расстояние R, называется радиусом молекулярного действия, а сферу радиусом R – сферой молекулярного действия.
Молекула, находящаяся внутри жидкости, испытывает одинаковое взаимодействие со стороны молекул, окружающих ее со всех сторон. Равнодействующая молекулярных сил, действующих на нее, будет равна нулю. Если же молекула расположена на поверхности жидкости, то равновесие нарушается: притяжение со стороны молекул, лежащих внутри жидкости больше и равнодействующая молекулярных сил направлена внутрь жидкости F1,2 . (рис 1).
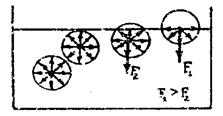
Рис.1
Молекулярные силы, действующие на все частицы, лежащие в тонком поверхностном слое, толщина которого равна радиусу сферы действия молекулы, складываясь между собой, оказывают на поверхность жидкости некоторое давление, которое называют молекулярным давлением. Все молекулы, находящиеся в поверхностном слое жидкости, подвержены действию этих сил, стремящихся втянуть их внутрь жидкости.
Таким образом, под действием молекулярных сил, направленных внутрь жидкости, поверхностный слой жидкости находится в особом, напряженном состоянии, напоминая собой напряжение растянутой пленки, стремящейся сократиться.
Чтобы переместить молекулу из глубины на поверхность жидкости, надо совершить работу против результирующей силы молекул в поверхностном слое. В результате молекулы на поверхности жидкости обладают определенной потенциальной энергией, называемой свободной поверхностной энергией. Если на жидкость не действуют внешние силы, то значение свободной поверхностной энергии оказывается минимальным; при этом минимальна и площадь и самой поверхности. Капли жидкости в невесомости имеют форму шариков (минимальная площадь поверхности). В земных условиях действует сила тяжести, которая пытается сдавить каплю, в результате чего она принимает форму эллипса.
Работа, которую нужно совершить для увеличения свободной поверхности жидкости будет равна:
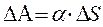
где α – коэффициент поверхностного натяжения.
По своему физическому смыслу α является работой, которую надо затратить, чтобы увеличить поверхность жидкости на единицу при сохранении ее объема неизменным. Коэффициент поверхностного натяжения α измеряется в системе СИ в Дж/м2.
Для того, чтобы поверхностную пленку удержать в равновесии, нужна определенная сила F, приложенная касательно к поверхности жидкости. Она будет тем больше, чем больше длина ℓ, ограничивающей поверхности пленки:
F = α *ℓ (1)
где α – коэффициент поверхностного натяжения.
Из формулы (1) следует, что
α = 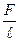 ,
,
т. е. коэффициент поверхностного натяжения жидкости численно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность жидкости. Из (2) видно, что α измеряется в Н/м. Коэффициент поверхностного натяжения жидкости имеет порядок 10-2- 10-1Н/м; для воды он равен 0,073 Н/м, а для ртути 0,54 Н/м. С повышением температуры коэффициент поверхностного натяжения уменьшается в связи с увеличением среднего расстояния между молекулами жидкости.
Когда жидкость налита в сосуд, то между молекулами стенок сосуда и молекулами поверхности жидкости действуют силы притяжения Fα (адгезии, т. е. силы прилипания молекул двух различных тел, вызванные взаимным притяжением), Fк они приводят к возникновению краевого угла θ между стенками сосуда и поверхностью жидкости. Равнодействующая сил когезии и адгезии Fα и Fк всегда перпендикулярна поверхности жидкости (рис. 2).
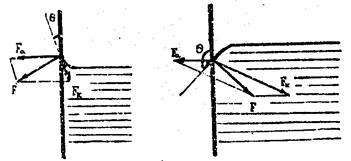
Рис.2
Из рис. 2 видно, что равнодействующая этих сил F может иметь различное направление, в результате чего поверхность жидкости может быть вогнутой, выпуклой или горизонтальной. Если жидкость смачивает стенки, то силы когезии Fк меньше, чем силы адгезии Fα; результирующая сила направлена из жидкости. В этом случае поверхность имеет вогнутую форму.
В не смачивающей жидкости, по аналогичным соображениям поверхность жидкости примет выпуклую форму.
Если Fα = Fк, то поверхность жидкости горизонтальна.
Под искривленной поверхностью жидкости, помимо внутреннего давления Р., создается еще дополнительное давление ΔР, обусловленное кривизной поверхности (рис. 3). Это добавочное давление всегда направлено к центру кривизны поверхности. Если жидкость имеет выпуклую поверхность, то добавочное давление направлено вовнутрь жидкости и общее давление в жидкости в этом случае будет больше, чем под горизонтальной поверхностью.
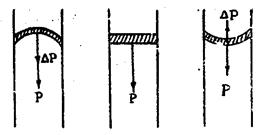
Рис.3
Если поверхность жидкости имеет вогнутую форму, то добавочное давление направлено к центру кривизны, находящемуся вне жидкости, и общее давление здесь меньше, чем под горизонтальной поверхностью.
Добавочное давление для сферической поверхности определяется по формуле Лапласа:
ΔР = 
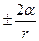 ,
,
где ΔР – добавочное давление,
α – коэффициент поверхностного натяжение,
r – радиус кривизны поверхности жидкости.
2. Описание экспериментальной установки:
В данной работе определения коэффициента поверхностного натяжения жидкости используется метод отрыва капель.
Испытуемая жидкость медленно по каплям вытекает из узкого отверстия тонкой стеклянной трубки (бюретки), установленной вертикально на штативе. Поверхностная пленка, образующаяся в отверстии, оказывает сопротивление вытеканию жидкости. Под давлением вышележащих слоев жидкости пленка растягивается, и жидкость собирается в каплю на конце трубки (рис.4).
На каплю действует сила тяжести P=mg , направленная вертикально вниз, и сила поверхностного натяжения F , действующая вверх. Пока капля удерживается на конце отверстия, сила Fбольше по величине, чем сила тяжести P. Так как жидкость вытекает из трубки, то капля будет увеличиваться в размере, и сила тяжести будет возрастать. Наступит такой момент, когда сила будет находиться в покле. Но как только Р. незначительно превысит силу поверхностного натяжения F, капля оторвется и упадет.
Пир вычислении считаем, что момент отрыва Р. = F, а силу поверхностного натяжения F можем определить по формуле (1):
F= α ℓ
где ℓ - длина контура, по которому разрывается поверхностный слой жидкости,
а он равен длине окружности в месте перетяжки (рис. 4).

Рис.4
Если радиус перетяжки обозначить через r, то ℓ=2πr и тогда запишем:
mg = α2πr
Тогда
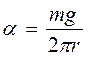 ,
,
Эта формула является расчетной для α.
3. Порядок выполнения работы:
1. Взвесьте на технических весах чистый сухой стаканчик и определите его массу m1.
2. Налейте в бюретку исследуемую жидкость.
3. Подставьте под бюретку второй стакан и отрегулируйте кран так, чтобы жидкость вытекала каплями (примерно 30 капель в минуту). 
4. Подставьте под бюретку взвешенный стаканчик: наберите в него n капель исследуемой жидкости (число капель задается преподавателем).
5. Определите массу стаканчика с каплями m2.
6. Вычислите массу одной капли по формуле:

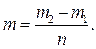
7. Опыт повторите 3 раза и найдите среднее значение массы одной капли m.
8. Вычислите коэффициент поверхностного натяжения по формуле (3) (радиус перетяжки написан на бюретке).
9. Рассчитайте ошибки измерений по формулам :
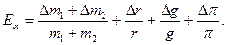
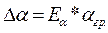
10.Данные измерений и вычислений занесите в таблицу I:
Таблица 1
Результаты эксперимента
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| Ср. |
11. Запишите ответ в виде:
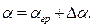
12.Сделайте выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Чем обусловлено возникновение дополнительного давления? Запишите формулу Лапласа.
2. Объясните молекулярно-кинетический механизм поверхностного натяжения.
3. От каких факторов зависит коэффициент поверхностного натяжения?
4. Что такое внутреннее давление жидкости?
5. Что такое поверхностно-активные вещества и где они применяются?
6. Объясните капиллярные явления. От чего зависит высота поднятия (опускания) столба жидкости в капилляре?
7. Выведите формулу Жюрена.
8. Объясните явления смачивания и несмачивания.
ЛАБОРАТОРНАЯ РАБОТА № 9
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА (Ср/Су) МЕТОДОМ КЛЕМАНА И ДЕЗОРМА
ЦЕЛЬ РАБОТЫ:изучение законов идеального газа, первого начала термодинамики, ознакомление с понятием газового цикла и определение отношения теплоемкостей воздух g = Ср/Сv
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:установка для определения отношения теплоемкостей.
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Теплоемкостью какого-либо тела Ст называется физическая величина,
численно равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один градус:
Ст = 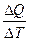
Теплоемкость единицы массы вещества называется удельной теплоемкостью и обозначается Суд.
Теплоемкость моля вещества называется молярной теплоемкостью и обозначается С.
Удельная и молярная теплоемкости связаны между собой соотношением:
Для газов удельная теплоемкость (а также молярная) существенно зависит  от условий, при которых производится нагревание газа. Если нагревание происходит при постоянном давлении, то все подводимое количество теплоты идет на увеличение внутренней энергии газа и работу по расширению газа. При нагревании газа при постоянном объеме работа по расширению газа не совершается и поэтому требуется меньшее количество теплоты. Поэтому для газов следует различать две удельные (а значит и молярные) теплоемкости –
от условий, при которых производится нагревание газа. Если нагревание происходит при постоянном давлении, то все подводимое количество теплоты идет на увеличение внутренней энергии газа и работу по расширению газа. При нагревании газа при постоянном объеме работа по расширению газа не совершается и поэтому требуется меньшее количество теплоты. Поэтому для газов следует различать две удельные (а значит и молярные) теплоемкости –
при постоянном давлении Ср и при постоянном объеме Су.
Молярная теплоемкость газа при постоянном объеме газа равна:
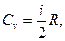
где i-число степеней свободы молекул газа,
R-универсальная газовая постоянная.
Молярная теплоемкость газа при постоянном давлении равна:
Ср.= 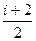
Отношение молярных теплоемкостей Ср/ Су. Обозначается γ и равно:
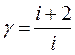
Из формулы видно, что γ зависит только от числа степеней свободы молекул газа. Напомним, что числом степеней свободы называется число независимых координат определяющих положение тела в пространстве. Для одноатомной молекулы число степеней свободы равно 3, для двухатомной – 5, для трехатомной молекулы – 6.
Отношение теплоемкости газа γ является важной характеристикой. Оно входит в уравнение Пуассона, описывающее адиабатические процессы.
Адиабатическими процессами называются такие процессы, при которых не происходит теплообмена газа, с окружающей средой. Очень быстро протекающие процессы, при которых не происходит теплообмена газа с окружающей его средой являются адиабатическими. По понятным соображениям, очень быстро протекающие процессы сжатия или расширения газа являются адиабатическими. Адиабатические расширения или сжатия газа сопровождаются изменением его внутренней энергии, а следовательно, и температуры.
При адиабатическом сжатии температура газа повышается, а при адиабатическом расширении-понижается.
Уравнение Пуассона можно записать через любую пару переменных: pV, T, PТ: 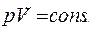
TV 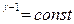
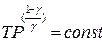
II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
Лабораторная установка (рис.1) состоит из стеклянного баллона Б, закрытого пробкой. В пробку вставлен стеклянный четверник, с помощью которого баллон соединен с манометром М, насосом Н и атмосферой (кран К). В шланг, соединяющий баллон с насосом, вставлен кран П, служащий для прекращения выхода воздуха после накачивания его в баллон.
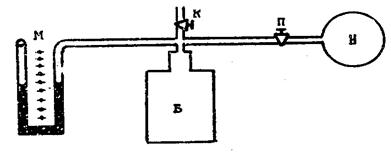
Рис.1
Рассмотрим ход опыта Клемана и Дезорма. Открыв кран П и закрыв кран К, насосом накачивают воздух в баллон, при этом воздух сжимается, а его температура и давление повышаются. Через некоторое время, благодаря теплопроводности стен баллона, воздух внутри него охладится до температуры окружающей среды, при этом в манометре установится некоторая разность уровней жидкости в правом и левом коленах. Обозначим разность уровней через разность h1. Она показывает, на сколько давление внутри баллона больше атмосферного.
Если обозначить атмосферное давление P0, то давление внутри баллон будет равно P0+h1 (конечно P0 и h1 должны быть выражены в одних и тех же единицах).
Значит, первое состояние газа можно описать следующими параметрами:
P0+h1 – давление воздуха внутри баллона,
V1 – объем некоторой массы воздуха внутри баллона,
Т1 – температура воздуха внутри баллона, равная температуре окружающей среды.
Откроем кран К на время, пока давление в баллоне не станет атмосферным (P0), при этом часть воздуха выйдет из баллона и в самом баллоне воздух расширится. Процесс расширения воздуха происходит достаточно быстро и его можно считать адиабатическим. Следовательно, газ совершат работу по расширению за счет уменьшения его внутренней энергии, а значит его температура понижается.
Тогда второе состояние газа можно описать параметрами:
P0 – Давление воздуха, равное атмосферному давлению,
V2 – объем газа,
Т2 – температура воздуха внутри баллона, ставшая меньше чем Т1.
Через некоторое время воздух внутри баллона нагревается до температуры окружающей среды, при этом его объем не изменяется, следовательно, увеличивается давление. В манометре установится некоторая разность уровней жидкости в правом и левом коленах.
Третье состояние газа можно описать следующими параметрами:
Р.о+h2 – давление воздуха внутри баллона,
V2 – объем газа,
Т1 – температура газа.
Сравнивая первое и третье состояние газа, можно заменить, что температуры одинаковы, следовательно, можно применить закон Бойля – Мариотта: «Для данной массы газа при постоянной температуре давление газа изменяется обратно пропорционально объему»:
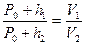 , (1)
, (1)
Переход газа из первого во второе состояние, как уже отмечалось, произошел адиабатически; следовательно, применим закон Пуассона в виде
PVγ = const:
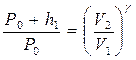 , (2)
, (2)
 Сопоставляя формулы (1) и (2), получим:
Сопоставляя формулы (1) и (2), получим:
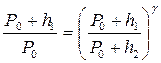 .
.
Прологарифмируем последнее выражение:
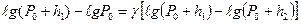 .
.
Из него найдем γ:
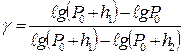 , (3)
, (3)
Так как давление Р0, Р0 + h1, Р0 +h2 незначительно отличаются друг от друга, то в формуле (3) отношение разности логарифмов можно заменить отношением разность самих чисел Р0, Р0 + h1, Р0 +h2. Тогда получим:
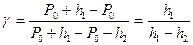 . (4)
. (4)
Формула (4) является расчетной для определения отношения теплоемкости.
2. Порядок выполнения работы:
1. Закройте кран К, откройте кран П и с помощью насоса накачайте воздух в баллон до некоторой разности уровней жидкости в манометре.
2. Когда уровни жидкости в манометре установится окончательно (т.е. газ в баллоне охладится до комнатной температуры), отсчитайте по шкале разности уровней в коленах манометра h1.
3. Быстро и полностью откройте кран К и закройте его как только уровни жидкости в коленах манометра сравняются.
4. Дайте время (~ 2 мин) установится уровням в коленах манометра. За это время температура воздуха в баллоне сравнивается с температурой окружающей среды. Отсчитайте разность уровней в коленах манометра h2.
5. Вычислите γ по формуле (3, 4).
6. Опыт повторите не менее 5-7 раз.
7. Рассчитайте ошибки измерений.
Еγ = 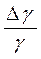
8. Результаты измерений занесите в таблицу 1:
Таблица 1
Результаты измерений
| № п/п | h1 | h2 | γ | Δγ | Eγ, % |
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| Сред. |
9. Сделайте выводы.
4. Контрольные вопросы:.
1. От чего зависит внутренняя энергия газа?
2. Какой процесс называется адиабатическим?
3. Напишите первое начало термодинамики и уравнение Пуассона. Поясните их.
4. Выведите соотношение Майера.
5. Напишите первое начало термодинамики и уравнение состояния для изохорического и изотермического процессов.
6. Изобразите на графике все изопроцессы.
7. Каков физический смысл газовой постоянной?
8. Сформулируйте экспериментальные газовые законы.
ЛАБОРАТОРНАЯ РАБОТА № 10
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА Ср/Сv МЕТОДОМ СТОЯЧИХ ЗВУКОВЫХ ВОЛН
ЦЕЛЬ РАБОТЫ:изучение законов идеального газа, первого начала термодинамики, ознакомление с понятием газового цикла и определение отношение теплоемкостей воздуха Ср/Сv.
ПРИБОРЫ И ПРИАДЛЕЖНОСТИ:звуковой генератор, осциллограф, измерительная труба с телефоном и микрофоном, термометр.
1. Краткие теоретические сведения:
Теплоемкость тела характеризуется количеством теплоты,необходимым для нагревание этого тела на один градус (Дж/град). Если для увеличения температуры тела на Т градусов необходимо сообщить ему ΔQ джоулей, то средняя теплоемкость тела в интервале ΔТ определяется как:
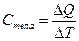 (1)
(1)
Теплоемкость тела пропорциональна массе и зависит от вещества тела. Удельная теплоемкость Суд данного вещества (дерева, железа, воздуха и т. д.) характеризуется количеством тепла на один градус, и измеряется в Дж/кг град. Удельная теплоемкость.
Для газов удобно пользоваться молярной теплоемкостью (Смол или просто С), характеризующейся количеством теплоты, нужным для нагревания одного киломоля данного вещества на один градус.
Очевидно, что
Суд/Дж/кг*град/*μ/кг/кмоль/ = С /Дж/кмоль*град/.
Поскольку в 1 киломоле любого газа содержится одинаковое количество молекул, а средняя кинетическая энергия молекул не зависит от их массы, то можно ожидать, что молярные теплоемкости всех достаточно разреженных газов должны быть одинаковыми.
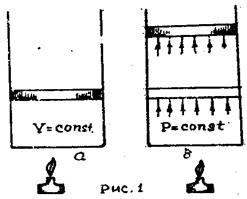
Теплоемкость тела существенно зависит от того, как меняются состояния тела в процессе нагревания. Рассмотрим для простоты идеальный одноатомный газ. Если мы будем нагревать газ, заключенный в замкнутом объеме, V = const (рис. 1, а), то все подводимое тепло ΔQ будет идти только на увеличение внутренней энергии газа. Тогда первое начало термодинамики при ΔA = 0 будет иметь вид: ΔQ = ΔU.
При этом температура газа будет возрастать в соответствии с увеличением его внутренней энергии, откуда следует, что температура идеального газа пропорциональна его внутренней энергии. Давление газа Р. также будет возрастать пропорционально температуре. Обозначим теплоемкость газа при постоянном объеме через С.
Если хотим, чтобы в процессе нагревания сохранилось давление, газу следует предоставить возможность расширяться. Для этого поместим газ в цилиндр с поршнем, на который действует постоянное давление Р. = const (рис. 1, б). Так как внутренняя энергия U идеального газа не зависит от его объема, то количество теплоты, необходимое для ее увеличения, останется тем же. Но при нагревании газа до той же температуры часть подводимого тепла расходуется теперь на работу против внешних сил при расширении газа. Следовательно, для нагревания газа до той же температуры, как и в предыдущем случае (V = const), придется затратить большее количество теплоты. Таким образом, теплоемкость ΔQ/ΔТ газа при постоянном давлении, которую мы обозначим через Ср., будет больше, чем СV.
Рассмотренный пример очень важен. Он показывает, что количество теплоты ΔQ, необходимое для нагревания газа на ΔТ градусов, существенно зависит от дополнительных условий – характера измерений других микроскопических параметров, определяющих состояние газа, т. е. Р. и V. Кроме рассмотренных процессов, характеризуемых простейшими дополнительными условиями V = const и Р. = const, можно рассмотреть и множество других, отвечающих различным изменениям V и Р. при нагревании. Каждому процессу будет отвечать своя теплоемкость С.
Величины Ср. и Сv для идеального газа оказывается связанными простым соотношением:
Ср. – Сv = R (2)
Это соотношение носит название закона Роберта Майера, полученного им в 1842 году.
Для идеального газа молярная теплоемкость при постоянном давлении превышают молярную теплоемкость при постоянном объеме на величину R т. е. на 8,31 кДж/кмоль град.
Универсальная газовая постоянная R численно равна работе расширения киломоля идеального газа при нагревании его на один градус при постоянном давлении.
Опыт показывает, что во всех случаях превращение механической энергии в тепловую и обратно совершается всегда в строго эквивалентных количествах. Поскольку тепловое движение есть в конечном счете, тоже механическое движение отдельных молекул (только не направленное, а хаотическое), то при всех этих превращениях должен соблюдаться закон сохранения энергии с учетом энергии не только внешних, но и внутренних движений. Такая общая формулировка этого закона носит название первого начала термодинамики и записывается в виде:
ΔQ = ΔU + ΔA, т. е.
Количество теплоты, сообщенное телу (ΔQ), идет на увеличение внутренней энергии (ΔU) и на совершение теплом работы (ΔА).
Однако, если сосуд с расширяющим газом теплоизолировать от окружающей среды, то теплообмен будет отсутствовать, т. е. ΔQ = 0. Процесс, происходящий при таком условии, называется адиабатическим. Уравнение первого начала термодинамики для адиабатического процесса тогда примет вид:
ΔQ = 0  0 = ΔU + ΔA или ΔА = - ΔU. (3)
0 = ΔU + ΔA или ΔА = - ΔU. (3)
Следовательно, при адиабатическом процессе работа совершается только за счет внутренней энергии газа. При адиабатическом расширении газ совершает работу, а его внутренняя энергия и, следовательно, температура падают. При адиабатическом сжатии работа газа отрицательная (внешняя среда производит работу над газом), внутренняя энергия и температура газа возрастают.
Теплоемкость при адиабатическом процессе будет равна 0, т. е.
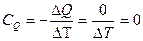
Уравнение, описывающее адиабатический процесс имеет вид:
PVγ = const ; где γ = СР/СV. (4)
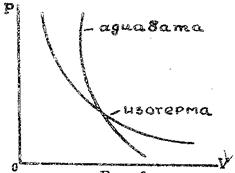
Рис.2
Так как СР>СV, то γ>1 и кривая, изображаемая уравнением (4), идет круче изотермы (рис. 2). Величина работы адиабатического процесса может быть особенно просто вычислена с помощью уравнения (3):

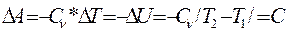
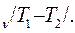
Для одноатомного газа С 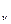 =12,5кДж/к моль град, Ср.=Сv+ =20,8 кДж/к моль град и показатель степени адиабаты γ=СР/Сv=1,67.
=12,5кДж/к моль град, Ср.=Сv+ =20,8 кДж/к моль град и показатель степени адиабаты γ=СР/Сv=1,67.
Для двухатомных газов при обычных температурах
g=29,1/20,8=1,4.
Для многоатомных газов γ еще ближе к единице.
В быстроходных двигателях внутреннего сгорания и при истечении газов через сопла реактивных двигателей процесс расширения газа протекает настолько быстро, что его можно считать практически адиабатическим и
рассчитывать по уравнению /4/.
Опыт также показывает, что для звуковых колебаний с минимальными частотами за время одного колебания /~0,1с/температура между сжатыми/ и тем самым разогретыми/ и разряженными /и тем самым охлажденными/ областями волны не успевает выравниваться. Практически процесс распространения звука можно считать адиабатическим, так что скорость распространения звука в идеальном газе определяется выражением :
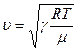 ,
,
где 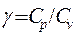
Отсюда легко найти 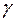 :
:

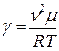 (5)
(5)
Таким образом, определение γ сводится к измерению скорости звука и абсолютной температуры воздуха. В данной работе скорость звука определяется методом стоячих волн - методом Кундта.
II. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ.
Схема экспериментальной установки изображена на рисунке 3. Телефон т, получая электрический сигнал от генератора1, излучает звуковые волны в трубу 2. Достигнув микрофона М, звуковая волна преобразуется в напряжение, которое поступает на вертикально отклоняющие пластины У электронного осциллографа 3.Напряжение на горизонтально отклоняющие пластины X подается непосредственно с выходных клемм звукового генератора. Телефон жестко закреплен на левом конце трубы, а микрофон может свободно перемещаться внутри нее.
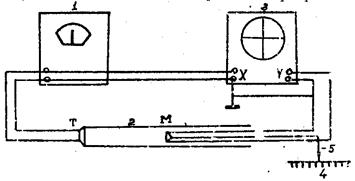
Рис.3
Фазовый сдвиг сигнала, поступающего на пластины У, относительно сигнала, подведенного к пластинам X зависит от времени, которое тратит звук на прохождение расстояния между микрофоном и телефоном, может быть использована для определения длины волны λ. При включении установки на экране осциллографа должен быть виден эллис. Изменяя расстояние между микрофоном и телефоном, можно добиться превращения эллипса в прямую линию. Если теперь сместить микрофон на λ/2, то на экране вновь возникнет прямая линия, проходящая на этот раз через другие квадранты. При дальнейшем смещении прямая вновь переменит свое направление и т.д. Таким образом, при помощи фигур, получивших название фигур Лиссажу, можно непосредственно измерить длину звуковой волны в воздухе и по формуле 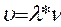 определить скорость звука, где
определить скорость звука, где 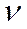 - частота генератора в Гц.
- частота генератора в Гц.
III.ПОРЯДОК ПРОВЕДЕНИЯ ИЗМЕРЕНИЙ.
1. Включите осциллограф и дайте ему прогреться в течение 10 минут.
2. Включите и настройте звуковой генератор на частоту 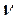 /частота задается преподавателем/.Установите напряжение на выходе генератора 1,5 В.
/частота задается преподавателем/.Установите напряжение на выходе генератора 1,5 В.
3. Установите указатель штока микрофона 5 в крайнее правое положение шкалы 4 /рис/, при этом на экране осциллографа появится фигура Лиссажу /эллипс или прямая линия/.
4. Перемещая шток с микрофоном в лево, зафиксируйте положение штока микрофона / 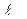 /, при которых эллипс превращается в четкую прямую линию, что соответствует узлам стоячей волны /отсчет производить в см по шкале 4/.
/, при которых эллипс превращается в четкую прямую линию, что соответствует узлам стоячей волны /отсчет производить в см по шкале 4/.
5. Вычислите разность между узловыми точками, которая является половиной длины волны 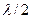 .
.
6. Вычислите длину волны 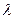 и скорость звуковой волны по формуле
и скорость звуковой волны по формуле 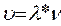 .
.
7. Определите термометром температуру окружающей среды.
8. Вычислите по формуле /5/.
9. Оцените погрешность измерений по формуле :

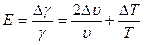 ;
; 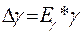

10. Результаты измерений занесите в таблицу :
Таблица 1
Результаты эксперимента
| 1. | |||||||||
| 2. | |||||||||
| 3. | |||||||||
| Ср. |
11.Сделайте выводы.
IV. КОНТРОЛЬНЫЕ ВОПРОСЫ.
Смотри работу №10.
ЛАБОРАТОРНАЯ РАБОТА № 11
| <== предыдущая страница | | | следующая страница ==> |
| Подготовка прибора к работе | | | ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ ВОЗДУХА |
Дата добавления: 2014-09-29; просмотров: 1310; Нарушение авторских прав

Мы поможем в написании ваших работ!