
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ОСНОВЫ МЕХАНИКИ
Учебно-методическое пособие
Самара
Самарский государственный технический университет

| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» |
Кафедра «Механика»
А.Б. КУБЫШКИН
ОСНОВЫ МЕХАНИКИ
Утверждено редакционно-издательским советом университета
в качестве учебно-методического пособия
Самара
Самарский государственный технический университет
УДК. 621
К 88
Р е ц е з е н т – канд. техн. наук, доц. Г.Н. Костина
Кубышкин А.Б.
К 88 Основы механики: учеб.-метод. пособ. / А.Б. Кубышкин. – Самара: Самар. гос. техн. ун-т, 2009. – 74 с.
Изложены основные положения курса «Механика» с примерами решения задач и контрольными вопросами к каждому разделу. Даны вопросы и задания для самопроверки и подготовки к экзаменам.
Предназначено для студентов немашиностроительных специальностей заочного обучения и может быть полезно при изучении дисциплин «Механика», «Прикладная механика» и «Техническая механика».
УДК. 621
К 88
Ó А.Б. Кубышкин, 2009
Ó Самарский государственный
технический университет, 2009
1. ОСНОВНЫЕ ПОНЯТИЯ О МАШИНАХ И МЕХАНИЗМАХ
1.1. Структура машин и механизмов
Большинство современных машин создается по схеме:
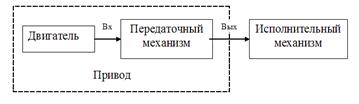
Машина – устройство, осуществляющее механические движения, необходимые для выполнения рабочего процесса с целью замены или облегчения физического и умственного труда человека.
Механизм является составной частью машины и представляет собой совокупность взаимосвязанных деталей и узлов, обеспечивающих выполнение заданных функций.
Привод состоит из двигателя и передаточного механизма. Он предназначен для обеспечения кинематических и силовых характеристик исполнительного механизма.
Передаточный механизм предназначен для передачи энергии от двигателя к исполнительному механизму с преобразованием вида и направления движения, а также изменения кинематических и силовых характеристик.
Исполнительный механизм предназначен для выполнения непосредственно рабочего процесса (обработка, транспортировка, перемешивание и др.).
1.2. Простые передачи. Основные характеристики и расчетные зависимости
Необходимость введения передаточного механизма обусловлена способностью выполнения им различных функций:
- передача энергии (мощности);
- преобразование (уменьшение или увеличение) сил или моментов сил;
- преобразование (уменьшение или увеличение) скорости движения звеньев;
- преобразование вида движения (вращательное в поступательное или наоборот) и изменение направления движения;
- разделение потоков движения от двигателя к нескольким исполнительным органам рабочей машины.
Среди передаточных механизмов широкое применение получили передачи вращательного движения, которые можно разделить на две основные группы:
- передачи, основанные на использовании сил трения (фрикционные, ременные);
- передачи, основанные на использовании зацепления (зубчатые, червячные, винтовые, цепные).
Рассмотрим простые передачи зацеплением, каждая из которых содержит два подвижных звена (валы с закрепленными на них зубчатыми колесами), совершающих вращательное движение, и одно неподвижное звено (опоры валов). На рис. 1.1 представлен внешний вид передач и варианты изображения на структурных схемах.
|
| ||||||
|
|
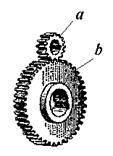
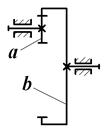
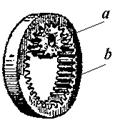
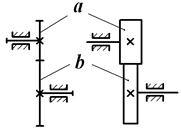
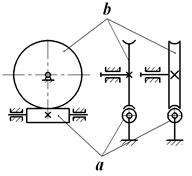
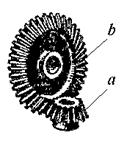
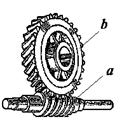
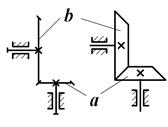
Рис. 1.1
Цилиндрические передачи характеризуются параллельным расположением осей зубчатых колес а и b и отличаются расположением зацепления: с внешним зацеплением и с внутренним зацеплением. В конической передаче оси зубчатых колес а и b пересекаются. В червячной передаче оси червяка а и червячного колеса b перекрещиваются.
Основной кинематической характеристикой передаточных механизмов является передаточное отношение U, которое представляет собой соотношение угловых скоростей w или частот вращения n входного (ведущего) а и выходного (ведомого) b звеньев. При этом обозначение передаточного отношения имеет два индекса, указывающие направление передачи движения от звена а к звену b:
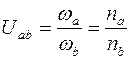 .
.
Частота вращения n связана с угловой скоростью w соотношением:
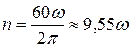 , об/мин.
, об/мин.
Передачи, уменьшающие скорость вращения, называются редукторами. В них передаточное отношение реализуется за счет соотношения диаметров d или числа зубьев Z ведомого b и ведущего а зубчатых колес в зацеплении:
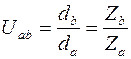 .
.
Таким образом, редукторы уменьшают скорость вращения в передаточное число раз за счет соотношения чисел зубьев зацепляемых колес:
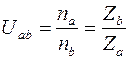 .
.
При этом ведущее зубчатое колесо в цилиндрических и конических передачах, имеющее меньшее число зубьев, называют шестерней, а ведомое – колесом.
Вращающий момент в редукторах увеличивается в передаточное число раз с учетом потерь на трение, оцениваемых коэффициентом полезного действия η:
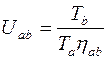 .
.
Коэффициент полезного действия (h) – это отношение полезной мощности Рn на выходном звене, расходуемой на реализацию полезной работы в производственном или технологическом процессе, к мощности на входном звене, затраченной двигателем 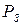 :
:
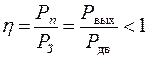 .
.
КПД учитывает потери мощности на преодоление сил трения в кинематических парах и является важным критерием оценки эффективности использования энергии и технического совершенства механизма.
При решении задач можно использовать следующие значения КПД для различных передач: цилиндрическая – η = 0,97; коническая – η = 0,96; червячная – η = 0,95 (1 – U / 200), где U – передаточное отношение в червячной передаче.
1.3. Многоступенчатые передаточные механизмы
При необходимости реализации передаточного отношения, величина которого превышает рекомендуемые пределы для отдельных передач, используют последовательное расположение передач (ступеней) в передаточном механизме.
В этом случае общее передаточное отношение (Uобщ) и общий КПД (hобщ) многоступенчатого передаточного механизма определяют как произведение передаточных отношений и КПД всех его ступеней (передач):
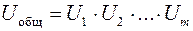 ;
;
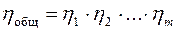 ,
,
где m – количество ступеней в механизме.
Передаточное отношение одной или группы ступеней m – ступенчатого механизма характеризует способность изменять частоту вращения n и вращающий момент Т при передаче движения между ведущим i и ведомым k звеньями рассматриваемой части механизма:
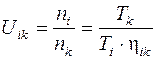 .
.
Полезную мощность на выходном валу механизма (Рвых, Вт) рассчитывают по зависимости:
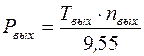 ,
,
где Твых, Нм и nвых, об / мин – соответственно вращающий момент и частота вращения выходного вала механизма.
Требуемую (расчетную) мощность двигателя ( 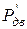 ) определяют с учетом потерь в узлах трения механизма:
) определяют с учетом потерь в узлах трения механизма:
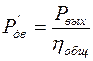 .
.
По расчетной мощности 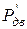 и частоте вращения
и частоте вращения 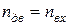 подбирают по каталогу стандартный электродвигатель, имеющий ближайшее большее значение мощности
подбирают по каталогу стандартный электродвигатель, имеющий ближайшее большее значение мощности 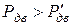 .
.
1.4. Примеры решения задач
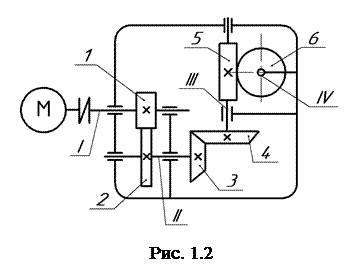 Задача 1.Провести структурный, кинематический и силовой анализ изображенного на рис. 1.2 привода, содержащего электродвигатель и редуктор.
Задача 1.Провести структурный, кинематический и силовой анализ изображенного на рис. 1.2 привода, содержащего электродвигатель и редуктор.
Заданы параметры:
– числа зубьев 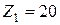 ,
, 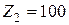 ,
, 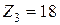 ,
, 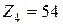 ,
, 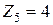 ,
, 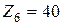 ;
;
– частота вращения вала двигателя 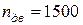 об/мин;
об/мин;
– вращающий момент на выходном валу редуктора 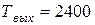 Нм.
Нм.
Решение
Структурный анализ. Трехступенчатый передаточный механизм образован путем последовательного присоединения трех отдельных передач.
Первая ступень – цилиндрическая передача с внешним зацеплением; оси шестерни 1 и колеса 2 параллельны.
Вторая ступень – коническая передача; оси шестерни 3 и колеса 4 пересекаются.
Третья ступень – червячная передача; оси червяка 5 и червячного колеса 6 перекрещиваются.
Оси входного I и выходного IV валов перекрещиваются.
Кинематический анализ. Определяем передаточные отношения:
– первой ступени: 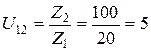 ;
;
– второй ступени: 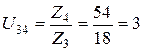 ;
;
– третьей ступени: 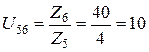 ;
;
– механизма: 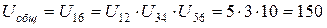 .
.
Определяем частоту вращения каждого вала механизма, учитывая, что зубчатые колеса закреплены на валах и имеют с ними одинаковые скорости:
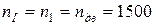 об/мин (по условию задачи);
об/мин (по условию задачи);
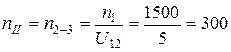 об/мин;
об/мин;
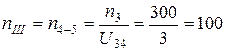 об/мин;
об/мин;
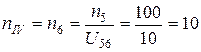 об/мин.
об/мин.
Силовой анализ. Определяем вращающие моменты на каждом валу:
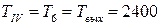 Нм (по условию задачи);
Нм (по условию задачи);
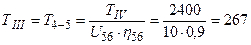 Нм.
Нм.
КПД червячной передачи определяем по зависимости:
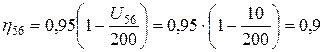 ;
;
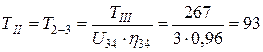 Нм;
Нм;
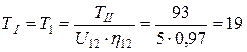 Нм.
Нм.
Таким образом, частота вращения валов уменьшается ступенчато в передаточное число раз ( 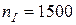 об/мин;
об/мин; 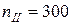 об/мин;
об/мин; 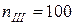 об/мин;
об/мин; 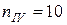 об/мин), а вращающие моменты увеличиваются (с учетом КПД) в передаточное число раз (
об/мин), а вращающие моменты увеличиваются (с учетом КПД) в передаточное число раз ( 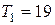 Нм;
Нм; 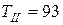 Нм;
Нм; 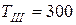 Нм;
Нм; 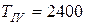 Нм).
Нм).
Рассчитываем полезную мощность по выходному валу редуктора:
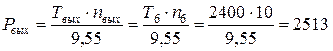 Вт = 2,5 кВт.
Вт = 2,5 кВт.
Требуемая (расчетная) мощность двигателя:
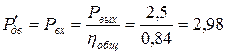 кВт,
кВт,
где 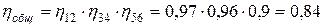 .
.
По каталогу подбираем стандартный электродвигатель 4А100S4 с частотой вращения 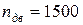 об/мин и мощностью
об/мин и мощностью 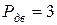 кВт.
кВт.
Задача 2.Провести кинематический анализ привода (см рис. 1.2 в задаче 1), используя другие исходные данные.
Заданы параметры:
– числа зубьев: 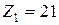 ,
, 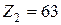 ,
, 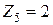 ,
, 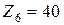 ;
;
– частота вращения вала двигателя: 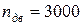 об/мин;
об/мин;
– частота вращения вала III редуктора: 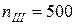 об/мин.
об/мин.
Решение
Определяем передаточные отношения:
– первой ступени: 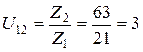 ;
;
– третьей ступени: 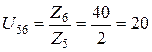 ;
;
– общее передаточное отношение первой и второй ступеней:
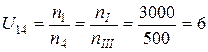 ;
;
– передаточное отношение второй ступени определяем, учитывая, что 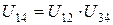 :
:
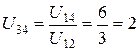 ;
;
– всего механизма: 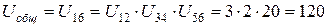 .
.
Определяем частоту вращения каждого вала механизма:
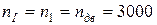 об/мин (по условию задачи);
об/мин (по условию задачи);
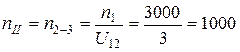 об/мин;
об/мин;
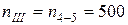 об/мин (по условию задачи);
об/мин (по условию задачи);
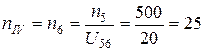 об/мин.
об/мин.
Таким образом, редуктор уменьшает частоту вращения вала двигателя в 120 раз (с 3000 об/мин до 25 об/мин), изменяя её ступенчато: в первой ступени в 3 раза (с 3000 об/мин до 1000 об/мин), во второй ступени в 2 раза (с 1000 об/мин до 500 об/мин) и в третьей ступени в 20 раз (с 500 об/мин до 25 об/мин).
Контрольные вопросы
1. Что такое привод, передаточный механизм, исполнительный механизм? Для чего они предназначены?
2. Какие функции может выполнять передаточный механизм?
3. Назовите простые передачи зацеплением и нарисуйте их структурные схемы. Какое взаимное расположение осей ведущего и ведомого звеньев характерно для каждой из передач?
4. Что такое передаточное отношение? Как оно характеризует передаточный механизм?
5. Что такое редуктор? Какие функции передаточного механизма он может выполнять? Как требуемое передаточное отношение реализуется в редукторах? Изобразите на схеме: цилиндрический редуктор с передаточным отношением 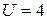 ; конический редуктор с
; конический редуктор с 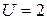 .
.
6. Составьте все возможные зависимости, по которым можно рассчитать передаточное отношение.
7. Что такое коэффициент полезного действия (КПД)? Как он характеризует передаточный механизм? Какие эксплуатационные параметры рассчитывают с учетом КПД?
8. Для чего предназначены многоступенчатые передаточные механизмы? Как определить общее передаточное отношение и общий КПД?
9. Решите задачу. Провести структурный, кинематический и силовой анализ изображенного на рис. 1.3 редуктора.
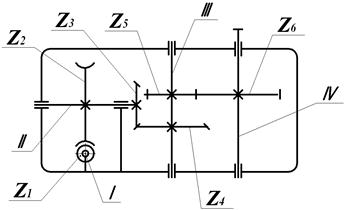 Заданы параметры:
Заданы параметры:
– числа зубьев 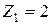 ,
, 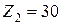 ,
, 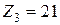 ,
, 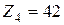 ;
;
– частота вращения валов
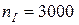 об/мин,
об/мин,
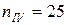 об/мин;
об/мин;
– вращающий момент
|
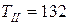 Нм.
Нм.
Определите:
а) количество ступеней в механизме;
б) тип передачи в каждой ступени;
в) передаточное отношение каждой ступени;
г) частоту вращения валов I и II;
д) вращающий момент на валах I, III, IV;
е) общее передаточное отношение;
ж) общий КПД;
з) мощность полезную и затраченную;
и) расположение осей входного I и выходного IV валов.
Ответы: а) 3; б) 1-Ч, 2-К, 3-Ц; в) 15, 2, 4; г) 200 и 100; д) 10, 253, 983; е) 120; ж) 0,82; з) 2,57 и 3,14; и) перекрещиваются.
2. ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ
2.1. Сила и момент силы.
Пара сил и момент пары сил
Статика – это раздел механики, в котором изучают условия равновесия звеньев механизма под действием сил.
Сила (F, Н) – мера механического взаимодействия твердых тел. Силу представляют в виде вектора 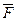 , действие которого характеризуется точкой приложения (например, т. А), направлением по линии действия и величиной F (рис. 2.1).
, действие которого характеризуется точкой приложения (например, т. А), направлением по линии действия и величиной F (рис. 2.1).
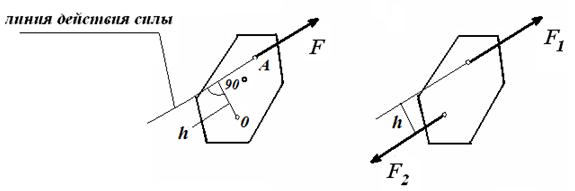
Рис. 2.1 Рис. 2.2
Пара сил (рис. 2.2) – система параллельных сил ( 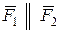 ), равных по модулю (F1 = F2) и направленных в противоположные стороны (
), равных по модулю (F1 = F2) и направленных в противоположные стороны ( 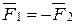 ).
).
Момент силы ( 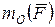 , Нм) относительно точки (например т. О) – это произведение численной величины силы F на плечо h – кратчайшее расстояние от точки до линии действия силы (см. рис. 2.1):
, Нм) относительно точки (например т. О) – это произведение численной величины силы F на плечо h – кратчайшее расстояние от точки до линии действия силы (см. рис. 2.1): 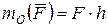
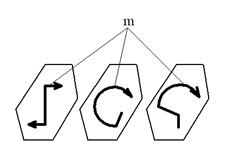 Момент пары сил (сосредоточенный момент) (m, Hм) определяется как произведение величины одной из сил на плечо пары h – расстояние между линиями действия сил (см. рис. 2.2):
Момент пары сил (сосредоточенный момент) (m, Hм) определяется как произведение величины одной из сил на плечо пары h – расстояние между линиями действия сил (см. рис. 2.2):
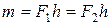 .
.
Рис. 2.3
|
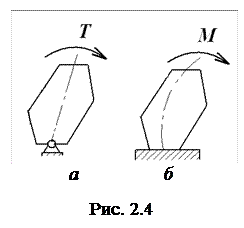
Вращающий момент (Т, Нм) – момент силы, действие которого сопровождается поворотом звена (рис. 2.4, а).
Изгибающий момент (М,Нм) – момент силы, действие которого сопровождается изгибом звена (рис. 2.4, б).
2.2. Связи и их реакции
Любой элемент конструкции или звено механизма является несвободным телом, перемещения которого в пространстве ограничивают другие тела, называемые связями. Связь, препятствующая перемещению несвободного тела, действует на него силой, называемой реакцией связи.
Направление реакций связей определяют на основании следующих правил:
1. Реакция связи прикладывается в точке контакта соприкасающихся поверхностей и направлена в сторону, противоположную тому направлению, в котором ограничивается перемещение.
2. Если связь ограничивает перемещение одновременно по нескольким направлениям, то направление реакции неизвестно и ее представляют в виде составляющих, направленных вдоль осей выбранной системы координат.
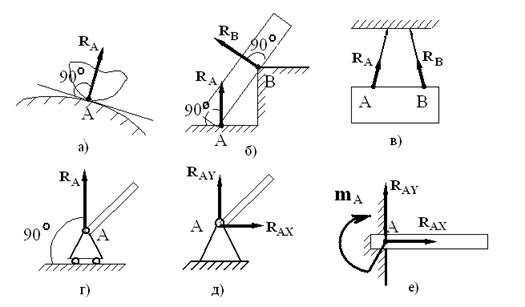
Рис. 2.5
Рассмотрим направление реакций для основных видов связей (рис. 2.5).
Контакт гладких поверхностей (рис. 2.5, а). Реакция 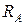 направлена по общей нормали к соприкасающимся поверхностям.
направлена по общей нормали к соприкасающимся поверхностям.
Контакт гладких поверхностей с угловыми точками и заострениями (рис. 2.5, б). Реакция направлена по нормали к гладкой поверхности.
Нерастяжимая нить (рис. 2.5, в). Реакции 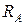 и
и 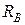 направлены вдоль нитей к точкам подвеса.
направлены вдоль нитей к точкам подвеса.
Шарнирно-подвижная опора (рис. 2.5, г). Реакция 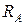 перпендикулярна опорной поверхности.
перпендикулярна опорной поверхности.
Шарнирно-неподвижная опора (рис. 2.5, д). Направление реакции 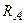 неизвестно. Представлена в виде неизвестных составляющих
неизвестно. Представлена в виде неизвестных составляющих 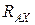 и
и 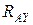 .
.
Жесткая заделка (рис. 2.5, е). В такой опоре может быть три составляющих реакции: 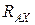 ,
, 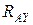 и опорный момент
и опорный момент 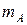 .
.
2.3. Условия равновесия плоской системы сил
Твердое тело находится в состоянии равновесия, если оно неподвижно относительно рассматриваемой системы отсчета.
Для равновесия твердого тела под действием произвольной системы сил необходимо и достаточно, чтобы главный вектор 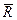 и главный момент
и главный момент 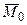 этой системы относительно любой точки О тела были равны нулю:
этой системы относительно любой точки О тела были равны нулю:
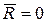 ;
; 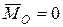 .
.
Главный вектор системы сил равен геометрической сумме всех сил системы:
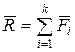 .
.
Главный момент системы сил равен сумме моментов всех сил относительно выбранного центра приведения 0:
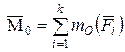 .
.
В результате условия равновесия имеют вид:
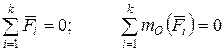 .
.
При решении практических задач используется аналитический метод решения векторных уравнений, согласно которому проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось.
В связи с этим представленные выше условия равновесия для плоской системы сил могут быть записаны в виде трех независимых уравнений равновесия твердого тела относительно прямоугольной системы координат XY:
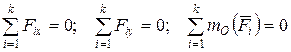 .
.
Твердое тело находится в равновесии, если алгебраическая (с учетом знака) сумма проекций всех сил на каждую из координатных осей равна нулю и алгебраическая сумма моментов всех сил относительно любой точки О плоскости XY равна нулю.
Для определения величины и направления реакции связи необходимо произвести следующие действия:
1) заменить внешние связи на их реакции, изобразив на силовой схеме их возможное направление;
2) из уравнений равновесия системы сил определить величину неизвестных реакций;
3) если в результате вычислений какая-либо реакция получается отрицательной, нужно изменить на схеме ее направление на противоположное;
4) произвести контрольную проверку правильности определения реакций как по величине, так и по направлению, используя дополнительно одно из уравнений равновесия, например уравнение моментов относительно не рассматриваемой ранее точки плоскости.
При составлении уравнений равновесия удобно использовать следующие положения:
– проекция вектора силы на ось равна произведению модуля (величины) силы на косинус угла между линией действия силы и осью, взятому со знаком плюс, если направления вектора и оси совпадают, или минус, если они противоположны:
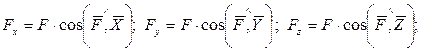
– момент силы берется со знаком плюс, если он действует в направлении движения часовой стрелки, и со знаком минус, если наоборот.
 2.4. Пример решения задач
2.4. Пример решения задач
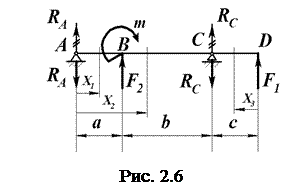
Задача. На рис. 2.6 изображена балка на двух шарнирных опорах А и С, нагруженная плоской системой внешних сил и моментов:
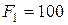 Н;
Н; 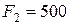 Н;
Н; 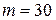 Нм;
Нм;
Размеры участков балки:
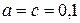 м;
м; 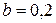 м.
м.
Требуется определить величину и направление векторов реакций опор 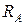 и
и 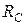 .
.
Решение
Изобразим на силовой схеме предположительное направление реакций опор 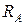 и
и 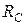 – оба вектора направлены вверх.
– оба вектора направлены вверх.
Определим величину и направление реакций 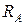 и
и 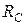 , используя уравнения равновесия плоской системы сил.
, используя уравнения равновесия плоской системы сил.
Составим уравнение моментов сил относительно опоры С, считая действие момента по направлению движения часовой стрелки положительным (со знаком «плюс»):
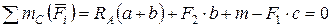 ;
;
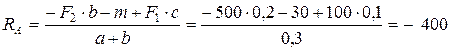 Н.
Н.
Знак «минус» свидетельствует о неправильно выбранном направлении 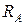 . Меняем на схеме направление вектора
. Меняем на схеме направление вектора 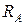 на противоположное.
на противоположное.
Реакция 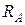 = 400 Н, направлена вниз.
= 400 Н, направлена вниз.
Составим уравнение проекций всех сил на вертикальную ось Y, считая направление вектора вверх положительным (со знаком «плюс»):
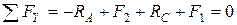 ;
;
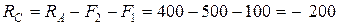 Н.
Н.
Знак «минус» свидетельствует о неправильно выбранном направлении 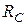 . Меняем на схеме направление вектора
. Меняем на схеме направление вектора 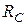 на противоположное.
на противоположное.
Реакция 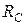 = 200 Н, направлена вниз.
= 200 Н, направлена вниз.
Проверяем правильность решения, используя дополнительное уравнение моментов сил относительно любой неопорной точки, например точки В:
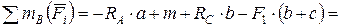
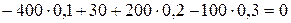 .
.
Полученный в результате вычислений «ноль» свидетельствует о правильности определения реакций 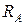 и
и  как по величине, так и по направлению.
как по величине, так и по направлению.
Контрольные вопросы
1. Дайте определение силы. Чем характеризуется действие силы?
2. Как определить момент силы относительно точки?
3. Дайте определение пары сил. Как найти момент пары сил? Как он обозначается на схемах?
4. Дайте определение вращающего и изгибающего моментов.
5. Что называется связью, реакцией связи?
6. Сформулируйте правила определения направления реакций связей.
7. Что называется главным вектором и главным моментом системы сил? Как они определяются?
8. Сформулируйте условия равновесия плоской системы сил; напишите уравнения равновесия.
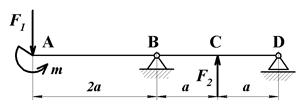 9. Решите задачу. На рис. 2.7 изображена балка на двух шарнирных опорах В и D, нагруженная силами
9. Решите задачу. На рис. 2.7 изображена балка на двух шарнирных опорах В и D, нагруженная силами 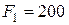 Н,
Н, 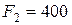 Н и сосредоточенным моментом
Н и сосредоточенным моментом 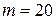 Нм. Размер
Нм. Размер 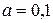 м. Определить величину и направление реакций опор
м. Определить величину и направление реакций опор 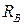 и
и 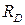 и произвести проверку.
и произвести проверку.
Ответ: 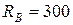 Н, направлена вверх;
Н, направлена вверх; 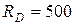 Н, направлена вниз.
Н, направлена вниз.
3. ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
3.1. Прочность, жесткость, устойчивость
Работоспособность конструкции зависит от прочности, жесткости и устойчивости составляющих ее элементов.
Прочность – способность конструкции и ее элементов воспринимать нагрузку без разрушения.
Жесткость – способность конструкции и ее элементов сопротивляться деформации, то есть изменению первоначальной формы и размеров под действием нагрузок.
Устойчивость – способность конструкции и ее элементов сохранять начальную форму упругого равновесия.
Большинство деталей механизмов рассчитывают на прочность, решая три основные задачи:
- определение рациональных размеров;
- определение безопасных нагрузок;
- выбор наиболее подходящих материалов.
При этом реальную конструкцию заменяют расчетной схемой, а результаты расчетов проверяют экспериментально.
3.2. Метод сечений. Внутренние силовые факторы
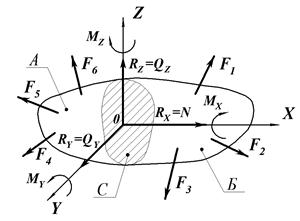 Внешние силы, действующие на элементы конструкций, разделяют на активные (нагрузки) и реактивные (реакции связей). Они вызывают появление внутренних сил сопротивления. Если внутренние силы превзойдут силы сцепления отдельных частиц материала, произойдет разрушение данного элемента конструкции. Следовательно, для оценки прочности изучаемого объекта необходимо знать внутренние силы и закон их распределения по объекту. Для решения этих задач используют метод сечений. Рассмотрим в равновесии элемент конструкции произвольной формы (рис. 3.1), нагруженный системой внешних сил
Внешние силы, действующие на элементы конструкций, разделяют на активные (нагрузки) и реактивные (реакции связей). Они вызывают появление внутренних сил сопротивления. Если внутренние силы превзойдут силы сцепления отдельных частиц материала, произойдет разрушение данного элемента конструкции. Следовательно, для оценки прочности изучаемого объекта необходимо знать внутренние силы и закон их распределения по объекту. Для решения этих задач используют метод сечений. Рассмотрим в равновесии элемент конструкции произвольной формы (рис. 3.1), нагруженный системой внешних сил 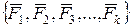 . В любом сечении этого элемента будут действовать внутренние силы, которые необходимо определить. Для этого мысленно рассечем рассматриваемый объект произвольно выбранным сечением на две части: А и Б.
. В любом сечении этого элемента будут действовать внутренние силы, которые необходимо определить. Для этого мысленно рассечем рассматриваемый объект произвольно выбранным сечением на две части: А и Б.
На каждую из этих частей будут действовать внешние силы 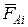 и
и 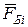 и внутренние силы в сечении
и внутренние силы в сечении 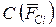 , уравновешивающие действие отсеченной части:
, уравновешивающие действие отсеченной части:
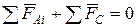 ;
; 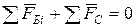 .
.
Следовательно, внутренние силы, возникающие в рассматриваемом сечении, равны сумме внешних сил, действующих на одну из отсеченных частей:
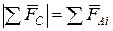 ;
; 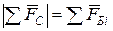 .
.
Как всякую систему сил, внутренние силы можно привести к одной точке, например к центру тяжести сечения О в виде главного вектора 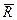 и главного момента
и главного момента 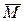 :
:
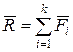 ;
; 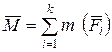 .
.
Проектируя действующие по одну сторону от сечения внешние силы 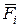 и моменты этих сил
и моменты этих сил 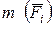 на выбранные оси координат, получают шесть уравнений равновесия, решением которых являются шесть внутренних силовых факторов:
на выбранные оси координат, получают шесть уравнений равновесия, решением которых являются шесть внутренних силовых факторов:

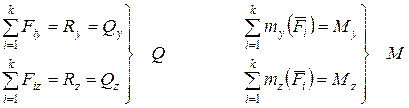
По виду деформации внутренние силовые факторы получили следующие названия:
– сила N, действующая по нормали к плоскости поперечного сечения, вызывает деформацию растяжения или сжатия в направлении продольной оси C и называется нормальной (продольной, осевой) силой;
– силы Q, действующие в плоскости поперечного сечения, вызывают деформацию сдвига (среза) в направлении поперечных осей Y (сила Qy ) и Z (сила Qz ) и называются поперечными (перерезывающими) силами;
– момент МХ, действующий вокруг продольной оси Х, вызывает деформацию кручения в плоскости поперечного сечения и называется крутящим моментом;
– моменты М, действующие вокруг поперечных осей Y (момент Мy) и Z (момент Мz) вызывают деформацию изгиба в плоскостях XZ и XY и называются изгибающими моментами.
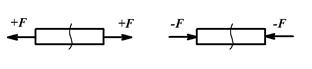
Таким образом, внутренние силовые факторы определяют как алгебраические суммы проекций внешних сил и моментов, действующих на рассматриваемую часть элемента конструкции. При этом следует учитывать правила знаков, графическая интерпретация которых представлена на рис. 3.2:
– продольная сила N считается положительной, если внешняя сила F растягивает сечение (направлена от сечения), и отрицательной, если сила F сжимает сечение (направлена на сечение);
– поперечная сила Q считаются положительной, если внешняя сила F стремится повернуть отсеченную часть относительно сечения по ходу часовой стрелки, и отрицательной, если – в противоположном направлении;
Продольная сила N Крутящий момент МХ
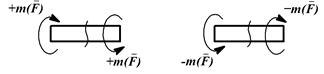
Поперечная сила Q Изгибающий момент M
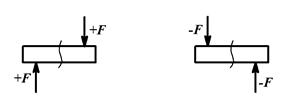
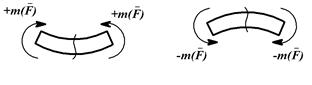
Рис. 3.2
– крутящий момент МХ считается положительным, если внешний вращающий момент 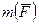 со стороны сечения направлен по часовой стрелке, и отрицательным при обратном направлении;
со стороны сечения направлен по часовой стрелке, и отрицательным при обратном направлении;
– изгибающий момент М считается положительным, если под действием внешнего изгибающего момента 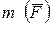 продольная ось изгибается выпуклостью вниз, и отрицательным, если выпуклостью вверх.
продольная ось изгибается выпуклостью вниз, и отрицательным, если выпуклостью вверх.
3.3. Эпюры внутренних силовых факторов
Учитывая, что в различных сечениях одного и того же элемента конструкции возникают разные силы и моменты, строят графики изменения внутренних силовых факторов, называемые эпюрами. Построение эпюр ведут в следующей последовательности.
1. Составляют расчетную схему изучаемого объекта и определяют (если необходимо) реакции связей из условия равновесия системы всех внешних сил (включая реакции).
2. Исследуемый объект размечают на участки, границами которых являются точки приложения сил, сосредоточенных моментов или пределы распределенной нагрузки.
3. Для произвольного сечения каждого участка составляют аналитические выражения внутренних силовых факторов, используя метод сечений и правила знаков.
4. Вычисляют значения внутренних силовых факторов на границах участков и для каждого из них строят эпюру.
5. Значения внутренних силовых факторов откладывают в выбранном масштабе и в направлении, перпендикулярном базовой (нулевой) оси эпюры.
6. Эпюры принято штриховать линиями, перпендикулярными базовой оси.
7. На эпюрах проставляют числовые значения внутренних силовых факторов в характерных сечениях и знак (плюс или минус).
8. Рядом с эпюрой напротив базовой оси пишут обозначение силового фактора и единицу его измерения.
3.4. Пример решения задач
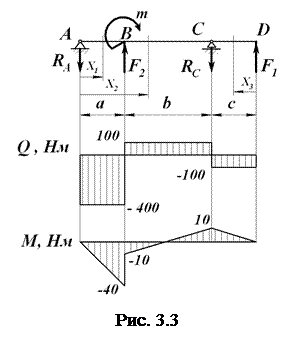
Задача. На рис. 3.3 изображена балка на двух шарнирных опорах А и С, на которую действуют силы активные (нагрузки 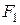 ,
, 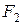 и момент
и момент 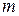 ) и реакции опор
) и реакции опор 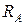 и
и 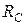 , рассчитанные из условия равновесия системы сил (см. пример п. 2.4).
, рассчитанные из условия равновесия системы сил (см. пример п. 2.4).
 Заданы параметры:
Заданы параметры: 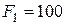 Н,
Н,
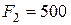 Н,
Н, 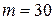 Нм,
Нм, 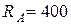 Н,
Н,
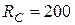 Н; размеры участков балки:
Н; размеры участков балки: 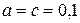 м,
м, 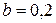 м.
м.
Требуется определить внутренние силовые факторы, действующие в поперечных сечениях балки, и построить эпюры поперечных сил 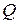 и изгибающих моментов
и изгибающих моментов 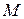 .
.
Решение
Выделим на схеме три характерных участка АВ, ВС и СD, границами которых являются точки приложения сил. Используя метод сечений, последовательно на каждом участке проводим произвольное поперечное сечение с координатой 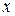 . Мысленно отбрасываем одну из отсекаемых частей балки (правую или левую), составляем уравнения равновесия для оставшейся части и определяем внутренние силовые факторы как алгебраическую сумму (с учетом правила знаков) всех внешних сил
. Мысленно отбрасываем одну из отсекаемых частей балки (правую или левую), составляем уравнения равновесия для оставшейся части и определяем внутренние силовые факторы как алгебраическую сумму (с учетом правила знаков) всех внешних сил 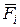 и моментов этих сил
и моментов этих сил 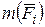 относительно сечения, действующих на рассматриваемую часть:
относительно сечения, действующих на рассматриваемую часть:
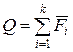 ;
; 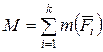 .
.
Участок АВ. Проводим сечение с координатой 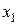 , изменяемой в пределах границ участка:
, изменяемой в пределах границ участка: 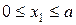 (начало координат в точке А). Из условия равновесия рассматриваемой части длиной
(начало координат в точке А). Из условия равновесия рассматриваемой части длиной 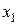 составляем выражения для поперечной силы
составляем выражения для поперечной силы 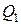 и изгибающего момента
и изгибающего момента 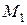 в сечении:
в сечении:
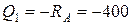 Н (постоянна на всем участке).
Н (постоянна на всем участке).
Эпюра поперечной силы 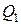 представляет собой прямую, параллельную базовой линии эпюры. Знак «минус» силы
представляет собой прямую, параллельную базовой линии эпюры. Знак «минус» силы 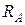 соответствует повороту рассматриваемой части балки относительно сечения против часовой стрелки (см. правила знаков):
соответствует повороту рассматриваемой части балки относительно сечения против часовой стрелки (см. правила знаков):
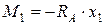 (изменяется по линейному закону).
(изменяется по линейному закону).
График изменения изгибающего момента 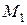 представляет собой наклонную прямую. Знак «минус» соответствует выпуклому изгибу балки. Значение момента достаточно вычислить для двух сечений, соответствующих границам участка АВ:
представляет собой наклонную прямую. Знак «минус» соответствует выпуклому изгибу балки. Значение момента достаточно вычислить для двух сечений, соответствующих границам участка АВ:
при 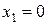
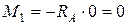 ;
;
при 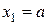
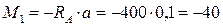 Нм.
Нм.
Полученные координаты в выбранном масштабе отмечаем по эпюре М (положительные значения откладываем вверх от базовой линии эпюры, а отрицательные – вниз) и соединяем их прямой линией.
Участок ВС. Проводим сечение с координатой 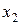 , изменяемой в пределах участка
, изменяемой в пределах участка 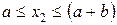 (начало координат остается в точке А). Для рассматриваемой части балки длиной
(начало координат остается в точке А). Для рассматриваемой части балки длиной 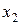 составляем выражения для поперечной силы
составляем выражения для поперечной силы 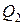 и изгибающего момента
и изгибающего момента 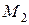 :
:
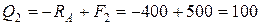 Н (постоянна на всем участке).
Н (постоянна на всем участке).
Эпюра поперечной силы 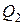 аналогична эпюре
аналогична эпюре 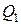 , так как значения
, так как значения 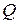 не зависят от координаты сечения
не зависят от координаты сечения 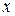 :
:
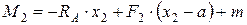 (изменяется по линейному закону).
(изменяется по линейному закону).
График изменения изгибающего момента 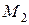 является наклонной прямой. Вычислим значение
является наклонной прямой. Вычислим значение 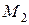 для граничных сечений участка ВС:
для граничных сечений участка ВС:
при 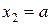
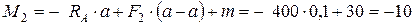 Нм;
Нм;
при 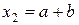
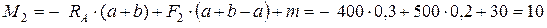 Нм.
Нм.
По полученным координатам строим эпюру М на участке ВС.
Участок СD. На этомучастке удобнее рассматривать правую отсеченную часть балки, мысленно отбрасывая левую часть. В этом случае выражения для 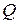 и
и 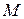 имеют более простой вид.
имеют более простой вид.
Проводим сечение с координатой 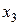 , изменяемой в пределах участка
, изменяемой в пределах участка 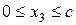 (начало координат переносим в точку D). Для рассматриваемой части балки длиной
(начало координат переносим в точку D). Для рассматриваемой части балки длиной 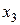 составляем выражения для поперечной силы
составляем выражения для поперечной силы 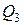 и изгибающего момента
и изгибающего момента 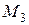 :
:
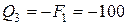 Н (постоянна на всем участке);
Н (постоянна на всем участке);
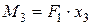 (изменяется по линейному закону).
(изменяется по линейному закону).
Вычисляем значения 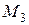 для граничных сечений участка СD:
для граничных сечений участка СD:
при 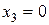
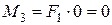 ;
;
при 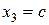
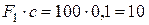 Нм.
Нм.
По полученным координатам строим эпюры 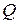 и
и 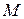 на участке СD.
на участке СD.
Для проверки правильности построения эпюр Q и M могут быть использованы их характерные особенности (при этом эпюры следует рассматривать слева направо):
– в сечениях, где к балке приложены сосредоточенные силы, на эпюре Q будут скачки: величина скачка равна величине силы, а направление указано вектором силы;
– в сечениях, где к балке приложены сосредоточенные моменты, на эпюре М будут скачки: величина скачка равна величине приложенного момента, а направление скачка будет положительным при направлении момента по часовой стрелке, и отрицательным – если наоборот;
– на участках, где нет распределенной нагрузки, эпюры Q ограничены прямыми, параллельными базовой оси эпюры, а эпюры М – наклонными прямыми;
– на участках, где 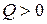 , эпюра М возрастает, а где
, эпюра М возрастает, а где 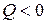 , эпюра М убывает;
, эпюра М убывает;
– в сечениях, где эпюра Q пересекает базовую ось ( 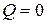 ), эпюра М имеет экстремальное значение.
), эпюра М имеет экстремальное значение.
Использование этих положений упрощает задачу построения эпюр Q и М: определяют внутренние силовые факторы для характерных точек (границ участков) и строят эпюры.
Контрольные вопросы
1. Дайте определения прочности, жесткости и устойчивости конструкции и её элементов. В чем их различия?
2. Ознакомьтесь с понятиями внешних и внутренних сил. В чем их различие? Как они связаны с оценкой прочности элементов конструкций?
3. Ознакомьтесь с назначением и сущностью метода сечений.
4. Какие внутренние силовые факторы могут возникнуть в поперечном сечении нагруженного стержня? Укажите их обозначения, направления и единицы измерения. Какие виды деформаций они вызывают?
5. Как определяют значения внутренних силовых факторов и знак (плюс или минус)? Запишите расчетные зависимости.
6. Что такое эпюры? Ознакомьтесь с методикой построения и оформления эпюр внутренних силовых факторов.
7. Решите задачу. На рис. 3.4 изображена балка на двух шарнирных опорах В и D. Известны: активные нагрузки 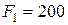 Н,
Н, 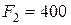 Н,
Н, 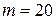 Нм и реакции опор
Нм и реакции опор 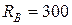 Н,
Н, 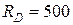 Н; размер
Н; размер 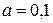 м.
м.
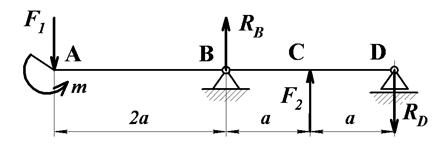
Рис. 3.4
Определите значения поперечных сил 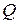 и изгибающих моментов
и изгибающих моментов 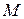 и постройте эпюры.
и постройте эпюры.
Ответ: 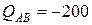 Н,
Н, 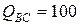 Н,
Н, 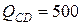 Н,
Н, 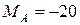 Нм,
Нм, 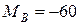 Нм,
Нм, 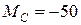 Нм,
Нм, 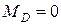 .
.
8. На рисунках показаны примеры построения эпюр продольных сил N (рис. 3.5), крутящих моментов MX (рис. 3.6), поперечных сил Q и изгибающих моментов М (рис. 3.7).
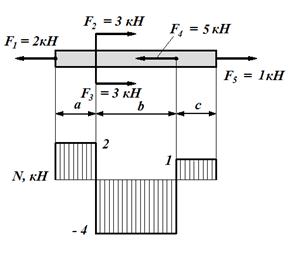
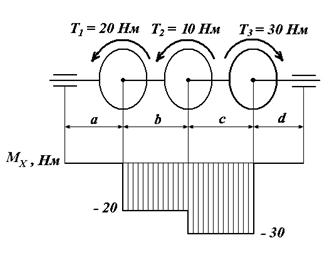
Рис. 3.5 Рис. 3.6
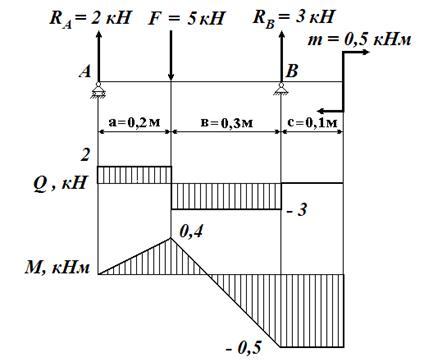
Рис. 3.7
Проверьте правильность построения эпюр, решив задачи в соответствии с примером п. 3.4 и используя положение о том, что скачки на эпюрах имеют место в сечениях, где приложены сосредоточенные нагрузки, а их величина равна величине соответствующей нагрузки (силы или момента сил).
4.НАПРЯЖЕННОЕ СОСТОЯНИЕ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И РАСЧЕТНЫЕ ЗАВИСИМОСТИ
4.1. Понятие о напряжениях и деформациях.
Закон Гука
Внутренние усилия возникают в каждой точке рассматриваемого сечения и распределяются по всей его площади. Интенсивность внутренних усилий в данной точке сечения называется напряжением и измеряется в единицах силы, отнесенных к единице площади: 1 Н/мм2 = 1 МПа. Напряжения, действующие по нормали к поверхности сечения, называются нормальными напряжениями и обозначаются s. Напряжения, действующие в плоскости сечения, называются касательными напряжениям и обозначаются t.
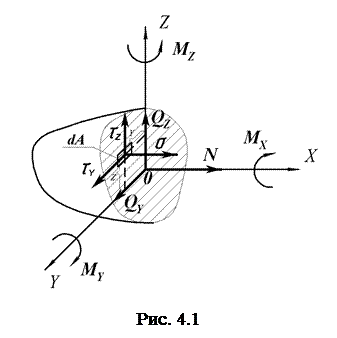
|
Связь внутренних силовых факторов с напряжением может быть выражена в виде шести интегральных зависимостей:
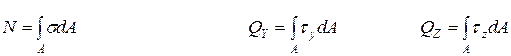
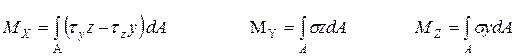
где dA – площадь бесконечно малого элемента сечения; y и z – координаты выделенного элемента сечения.
Анализ интегральных зависимостей показывает, что при растяжении, сжатии или изгибе в сечении действуют нормальные напряжения s, а при сдвиге или кручении – касательные напряжения t.
Действие эксплуатационных нагрузок приводит к изменению формы и размеров элементов конструкции. Эти изменения называют деформацией.
Деформация, исчезающая после снятия нагрузки, называется упругой, а неисчезающая деформация называется остаточной, или пластической.
Перемещение сечений вдоль прямой линии называется линейной деформацией, а поворот сечений – угловой деформацией.
Изменение линейного размера 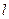 (рис. 4.2) характеризуется абсолютной деформацией
(рис. 4.2) характеризуется абсолютной деформацией 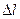 (измеряется в мм) и относительной деформацией
(измеряется в мм) и относительной деформацией 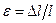 (величина безразмерная).
(величина безразмерная).
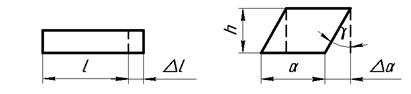
Рис. 4.2 Рис. 4.3
Изменение формы (рис. 4.3) характеризуется абсолютной сдвиговой деформацией 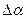 и относительной угловой деформацией (углом сдвига)
и относительной угловой деформацией (углом сдвига) 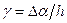 .
.
Английским ученым Р. Гуком была установлена линейная зависимость между напряжениями и деформациями, обусловленная упругими свойствами материалов. Закон Гука имеет вид:
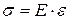 ;
; 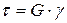 ,
,
где E и G – коэффициенты пропорциональности, являющиеся физическими константами материалов: Е – модуль продольной упругости (модуль Юнга); G – модуль сдвига.
4.2. Простые виды деформаций. Основные характеристики и расчетные зависимости
Все разнообразие форм элементов конструкций можно разделить на четыре типа: стержни, пластины, оболочки и пространственные тела.
Рассмотрим их напряженно-деформированное состояние на примере стержней в случаях, когда в поперечном (перпендикулярном оси) сечении действует только один из шести внутренних силовых факторов.
Растяжение-сжатие. Деформация, при которой в поперечных сечениях стержня действует только продольная растягивающая или сжимающая сила (рис. 4.4), называется растяжением или сжатием.
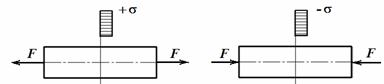
Рис. 4.4
Продольная сила N , приложенная в центре тяжести сечения, является равнодействующей нормальных напряжений s, равномерно распределенных по сечению и рассчитываемых по зависимости
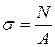 ,
,
где А – площадь поперечного сечения.
Растягивающие напряжения считаются положительными (+s), а сжимающие – отрицательными (-s).
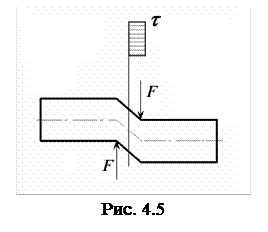 Сдвиг (срез). Деформация, при которой в поперечных сечениях стержня действует только поперечная (перерезывающая) сила (рис. 4.5), называется сдвигом. Поперечная сила Q действует в плоскости сечения и является равнодействующей касательных напряжений t, равномерно распределенных по сечению и рассчитываемых по зависимости
Сдвиг (срез). Деформация, при которой в поперечных сечениях стержня действует только поперечная (перерезывающая) сила (рис. 4.5), называется сдвигом. Поперечная сила Q действует в плоскости сечения и является равнодействующей касательных напряжений t, равномерно распределенных по сечению и рассчитываемых по зависимости
|
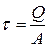 ,
,
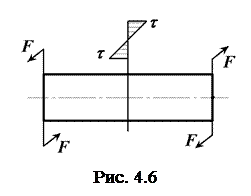 где А – площадь поперечного сечения.
где А – площадь поперечного сечения.
Кручение. Деформация, при которой в поперечных сечениях стержня действует только крутящий момент (рис. 4.6), называется кручением.
Крутящий момент MX действует в плоскости сечения и является равнодействующим моментов касательных напряжений t относительно продольной оси стержня.
Деформация кручения имеет сдвиговый характер и является результатом взаимного поворота поперечных сечений. При этом касательные напряжения распределяются по линейному закону: равны нулю в центре сечения и достигают максимума на его внешнем контуре. Наибольшее значение напряжений в сечении рассчитывают по зависимости
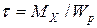 ,
,
где Wp – полярный момент сопротивления сечения. При действии на стержень постоянного по величине момента Т расчетная зависимость имеет вид
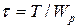 .
.
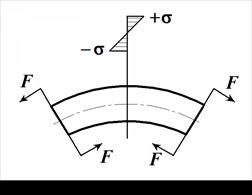 Изгиб. Деформация, при которой в поперечных сечениях стержня действует только изгибающий момент (рис. 4.7), называется чистым изгибом.
Изгиб. Деформация, при которой в поперечных сечениях стержня действует только изгибающий момент (рис. 4.7), называется чистым изгибом.
|
Наибольшее значение напряжений в сечении рассчитывают по зависимости
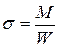 ,
,
где W – осевой момент сопротивления сечения.
Расчетные зависимости геометрических характеристик различных форм сечений представлены в справочной литературе. Для круглых сечений диаметра 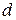 расчетные зависимости имеют вид:
расчетные зависимости имеют вид:
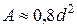 ;
; 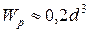 ;
; 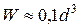 .
.
Связь внутренних силовых факторов с деформациями и напряжениями для наглядности можно представить в виде схемы (рис. 4.8).

Рис. 4.8
4.3. Сложное сопротивление. Поперечный изгиб, изгиб с растяжением, изгиб с кручением
Сложное сопротивление имеет место в тех случаях, когда в поперечных сечениях нагруженного стержня одновременно действуют несколько внутренних силовых факторов. В расчетах используется принцип суперпозиции – принцип независимости действия сил, согласно которому результат действия группы сил на тело равен сумме результатов действия каждой силы в отдельности и не зависит от последовательности нагружения. Таким образом, определяют значения напряжений от каждого силового фактора отдельно, устанавливают наиболее нагруженные
| <== предыдущая страница | | | следующая страница ==> |
| Выполнила студентка 5 курса Алина Гагаринова | | |
Дата добавления: 2014-09-29; просмотров: 727; Нарушение авторских прав

Мы поможем в написании ваших работ!