Представление эпидемиологических данных

Представление эпидемиологических данных предусматривает целе­направленные и разнообразные действия по оформлению эпидемиоло­гических данных, т.е. «организацию эпидемиологических данных». Ор­ганизацией эпидемиологических данных предусматривает составление таблиц, построение диаграмм.

В описательной эпидемиологии правильно построенные таблицы и диа­граммы позволяют в беспорядке цифр выявить и описать различные прояв­ления динамики и структуры заболеваемости, первоначально скрытые в этих цифрах. Без таблиц и диаграмм невозможна логическая обработка эпидеми­ологических данных и выдвижение гипотез о факторах риска. Кроме того, таблицы и диаграммы необходимы для того, чтобы в доходчивой форме отразить результаты исследований и донести их до заинтересованных лиц.

Таблицы

Таблица — перечень данных, приведенных в определенную систему и разнесенных по графам (колонкам и строкам). Всесторонняя характе­ристика требований, предъявляемых к таблицам, может быть выражена термином «самообъясняющая, самодостаточная таблица». Это значит,

что любая таблица, изъятая из текста, обязана передавать ту же инфор­мацию, что и в сочетании со связанным с ней текстом. Требования, предъявляемые к оформлению таблиц.

• Таблица должна иметь порядковый номер, четкий заголовок, отражаю­щий диагноз, признаки времени, места возникновения заболеваний и при­знаки «лица».

• В названии таблицы или непосредственно в ней самой должны быть обоз­начены единицы измерения признака по строкам и колонкам.

• В таблицах должно быть подлежащее и сказуемое. Эпидемиологическое подлежащее — это основной группированный признак заболеваемости (т. е. то, о чем говорят в таблице), его обычно располагают по строкам таблицы. Эпидемиологическое сказуемое — это группировочные при­знаки, детализирующие подлежащее, их обычно располагают по колон­кам (столбцам) таблицы.

• Там, где это возможно, должны быть проставлены суммы по строкам и колонкам.

• При необходимости в конце таблице помещают примечание, состоящее из дополнительных разъяснений, облегчающих восприятие таблицы.

• Если таблица (или часть ее) заимствована, следует указать источник информации.

По особенностям группировки различают простые, групповые и ком­бинационные (сложные) таблицы.

• Простые таблицы, или таблицы с одной переменной. В таких таблицах группируют лишь подлежащее (строки), т. е. одну переменную. Такой переменной может быть признак времени, признак места или признак лица. В простой таблице может быть несколько столбцов, отражающих абсолютные числа и соответствующие им относительные величины.

• Групповые таблицы, или таблицы с двумя переменными. Данные груп­пируют по признакам, представленным и в подлежащем (строки), и в сказуемом (столбцы). В сказуемом может быть одновременно несколько признаков, например пол, возраст, профессия, место жи­тельства и т. д. При этом каждый такой признак (в столбце) сочетают с подлежащим (в строке) только попарно. Такие таблицы в зарубеж­ных изданиях называют таблицами сопряженности признаков.

• Комбинационная таблица. Данные сочетают по трем группировочным признакам и более. Такие таблицы труднее воспринимать и поэтому их, как правило, используют только на стадии сбора и первичной об­работки информации. Их также называют разработочными, или ра­бочими таблицами.

Диаграммы

Диаграммы — обязательный элемент оформления эпидемиологичес­ких данных. Виды диаграмм:

• линейные;

• столбиковые;

• круговые;

• картограммы;

• картодиаграммы (сочетания различных видов диаграмм). Большинство диаграмм легко строить и запоминать, но вместе с тем

высока вероятность неправильного прочтения. Случайно или преднаме­ренно неправильно построенные диаграммы способны, особенно у не­подготовленной аудитории, создать ошибочное представление о прояв­лениях заболеваемости.

Особенности оформления диаграмм:

• диаграмма должна иметь порядковый номер, четкий заголовок, отра­жающий диагноз, признаки времени, места возникновения заболеваний, признаки «лица» и единицы измерения признака;

• оси диаграмм должны иметь обозначения признаков. Па вертикальной оси (в ленточных столбиковых диаграммах — на горизонтальной) ука­зывают цену деления масштабного отрезка и размерность признака;

• площадь диаграммы можно заполнять дополнительными данными, помо­гающими ее прочтению;

• при необходимости в конце диаграммы помещают примечание из допол­нительных разъяснений, облегчающих восприятие;

• если диаграмма заимствована, следует указать источник информации. Применение компьютеров значительно упростило процесс построе­ния диаграмм и разнообразило способы графического отображения эпи­демиологических данных. Однако не следует злоупотреблять возмож­ностями компьютерной графики и в погоне за красочностью диаграммы перегружать ее элементами, затрудняющими прочтение.

Линейные диаграммы

Линейные диаграммы (графики) отображают количественные данные в системе двух прямоугольных координат: оси X (горизонтальная ось) и оси У (вертикальная ось). При этом в эпидемиологии линейные диа­граммы необходимы главным образом для отображения динамики забо­леваемости, т. е. ее изменения во времени.

Для построения графиков используют три типа шкал: арифметичес­кую, логарифмическую и временную.

Отличительные признаки арифметической шкалы (рис. 2-3):

одинаковая длина всех основных масштабных отрезков (делений);

одинаковая длина всех промежуточных масштабных отрезков (делений);

значение каждого последующего основного масштабного отрезка от­личается от предыдущего на величину цены деления; цена деления любого основного отрезка соответствует цифре, проставленной у пер­вого основного отрезка (см. рис. 2-3, цена деления основного отрезка арифметической шкалы равна 12);

в большинстве случаев начало шкалы — значение 0 (ноль). Отличительные признаки логарифмической шкалы (см. рис. 2-3): одинаковая длина всех основных масштабных отрезков (делений), стандартная длина отрезка — 10 см;

различная длина всех промежуточных масштабных отрезков (делений) в пределах одного основного масштабного отрезка; их длина посте­пенно уменьшается от начала основного отрезка к его концу, при этом вся «насечка» промежуточных делений в разных основных отрезках остается одинаковой;

цена каждого основного деления равна 10 в степени «n» (10ⁿ), поэтому значение каждого последующего основного масштабного отрезка от­лично от предыдущего в 10 раз (если нет разрывов шкалы); начало шкалы — любое значение 10ⁿ.

Временная шкала (см. рис. 2-3) похожа на арифметическую, но на ней отсутствуют промежуточные деления.

При построении графиков на оси X, как правило, обозначают время, а на оси У отражают показатели заболеваемости или абсолютные числа заболевших. При этом на ось У наносят чаще арифметическую, реже ло­гарифмическую шкалу. Графики, построенные с использованием по оси У арифметической шкалы, будем сокращенно называть — арифмети­ческие графики. Графики, построенные с использованием логарифми­ческой шкалы только по оси У, будем называть — полулогарифмические графики.

Линейные диаграммы позволяют наглядно (это и определило их ши­рокое распространение) отразить различие показателей одной или не­скольких кривых и особенности их динамики, правда, не всегда кор­ректно.

Интерполяция — отыскание неизвестных промежуточных значений какой-либо величины по известным ее значениям. Поскольку годовые (месячные) показатели заболеваемости — кумулятивные (накопление аб­солютного числа заболеваний к концу года, месяца), то в любой проме­жуток времени внутри года (например, в средине) заболеваемость не мо­жет быть выше, чем в конце этого года.

К примеру, на первый взгляд технически легко оценить заболеваемость гепатитом А в середине 1997 г., проведя соответствующие вертикаль­ные и горизонтальные линии и «сняв» значение заболеваемости с оси У. Получим цифру, равную приблизительно 70,0%ооо> однако возникнет аб­сурдная ситуация: в середине 1997 г. интерполируемый показатель заболе­ваемости (70,0%ооо) выше, чем в конце того же года (50,4°/ооо0), a такого, естественно, быть не может. Учитывая кумулятивный характер показате­лей заболеваемости, их динамику корректней (но менее привычно) отоб­ражать в виде гистограмм.

Арифметические графики

Арифметические графики — наиболее распространенная разновид­ность линейных диаграмм, иллюстрирующих особенности распреде­ления заболеваемости во времени, например по годам, месяцам, не­делям или дням. Они всегда демонстративно передают разницу между показателями одной кривой (рис. 2-4), и разницу показателей не­скольких кривых, если различия уровней заболеваемости не превыша­ют 100 раз (рис. 2-5).

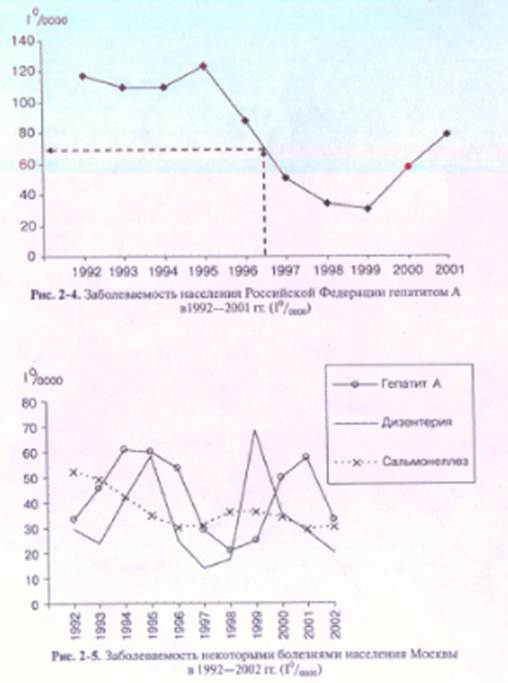
Общее правило построения арифметических графиков: длина графика (площади диаграммы) по горизонтали должна быть несколько больше длины графика по вертикали. Однако как бы не были нарушены пра­вила построения таких графиков, большие величины всегда располагают выше меньших. Пересечение оси Y и оси X происходит в точке со значе­нием 0 (ноль).

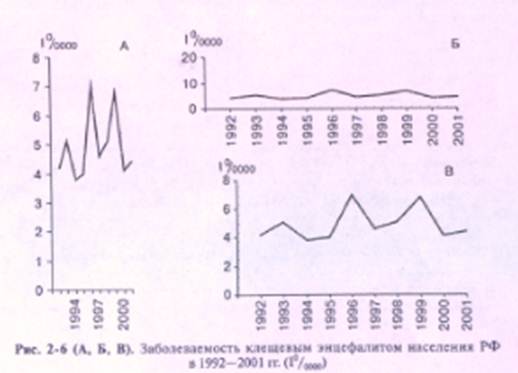
Если на графиках отсутствуют данные, позволяющие оценить досто­верность различий показателей заболеваемости (это правило для всех видов диаграмм), необходима осторожность в формулировании даже ориентировочных выводов об особенностях тенденций и колебаний за­болеваемости. В зависимости от соотношения размера арифметического графика по оси X и оси Y, кривые, построенные по одним и тем же дан­ным, могут выглядеть по-разному (рис. 2-6, рис. 2-7).

Приведенные рисунки (см. рис. 2-6 (А, Б, В), отражающие динамику годовых показателей, построены по одним и тем же данным. Заметим, в одном случае (см. рис. 2-6 А) возникает впечатление значительно более выраженных колебаний годовых показателей заболеваемости клещевым энцефалитом населения РФ в 1992—2001 гг., чем в другом (см. рис. 2-6 Б).

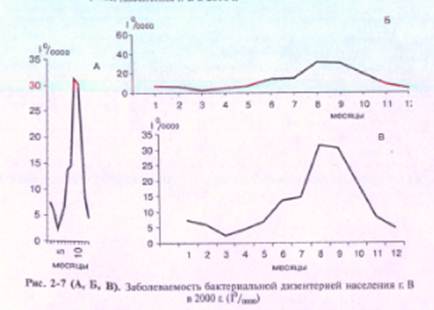
Pисунки (рис. 2-7 А, рис. 2-7 Б) также построены по одним и тех же месячным показателям, но они создают разное и ложное представление об особенностях внугригодовой динамики заболеваемости бактериаль­ной дизентерией населения г. В в 2000 г.

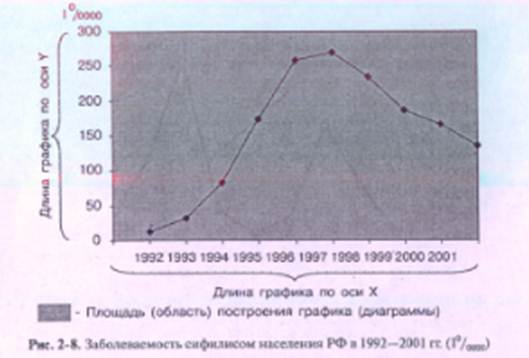
Оптимальным для изучения динамики показателей (их тенденции, наличия или отсутствия колебаний) будет построение арифметических графиков, основанное на принципе «золотого сечения» (см. рис. 2-6 В, рис. 2-7 В). Согласно этому правилу, длина графика (площади его пост­роения) по оси У должна относиться к длине графика по оси X как 1 :^/2 или приблизительно как 1:1,5 (рис. 2-8).

Такой прием значительно уменьшает субъективизм прочтения арифме­тических графиков, но не во всех случаях способен предотвратить возмож­ные ошибки прочтения диаграмм. Это, прежде всего, актуально при оценке колебаний годовых показателей заболеваемости нескольких групп населе­ния, когда на одном рисунке размещены хотя бы две кривые, образован­ные резко (в 1 00 раз и более) различающимися показателями. В резуль­тате для кривой с меньшими показателями нарушено правило «золотого сечения»: она «прижимается» к горизонтальной оси и возможные колеба­ния показателей заболеваемости могут быть неразличимы. Так возникает ложное впечатление, что для взрослых, в отличие от детей, нехарактерны колебания заболеваемости краснухой (см. рис. 2-9).

Возможно такое же ошибочное представление о наличии (отсутствии) колебаний показателей заболеваемости может возникнуть и при анализе одной кривой, отражающей, например, резкое снижение заболеваемости после введения массовой плановой иммунизации населения (рис. 2-10).

Так, отчетливо видны два периода с настолько различными уровнями заболеваемости, что часть кривой, начиная с 1970 г., оказывается «прижа­той» к оси X. При сравнении колебаний показателей в разные периоды может быть сделан ошибочный вывод об относительно равномерном рас­пределении показателей заболеваемости с 1970 по 2001 гг.

Чтобы избежать ошибочных выводов при изучении особенностей колебаний годовых показателей заболеваемости, необходимо выбрать оптимальный способ отображения табличных данных, позволяющий проявить возможные колебания показателей заболеваемости в ситуа­циях, обозначенных рис. 2-9 и рис. 2-10. В таких случаях рекомендуют использовать дополнительную (вспомогательную) ось У (ее располагают в правой части графика) для одной из двух кривых (рис. 2-11) или части одной кривой (рис. 2-12).

На представленном рис. 2-11 отчетливо видно (сравните с рис. 2-9), что и для детей, и для взрослых характерны выраженные колебания забо­леваемости краснухой: кривые фактически повторяют друг друга, но на разных уровнях.

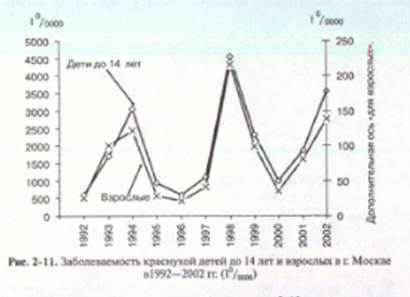
Дополнительная (вспомогательная) осьнарис.2-12 позволяет увидеть (в отличие от рис. 2-10), что и для периода с 1970 по 2001 г., несмотря на значительно меньшую частоту заболеваний, характерны колебания забо­леваемости коклюшем. Хотя, конечно, абсолютная разница показателей в период до и после введения вакцинации существенна. До введения при­вивок заболеваемость коклюшем населения РФ в годы подъемов и спа­дов различалась в сотни случаев на ЮОтыс. человек, а в поствакциналь­ный период колебания заболеваемость составляла только десятки случаев в той же размерности.

Конечно, если тщательно изучать рис. 2-12 только по основной оси, можно сделать тот же вывод об особенностях колебаний показателей. Од­нако иногда без вспомогательной оси невозможно по арифметическому графику сделать правильные выводы.

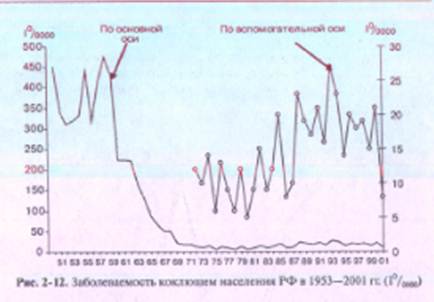
Только анализ динамики кривой по дополнительной оси рис 2-13 позво­ляет увидеть, что и в 1970—1990 гг., несмотря на очень низкие показатели заболеваемости дифтерией, отмечены их колебания. Кроме того, отчетливо видно, что начало формирования тенденции роста заболеваемости дифте­рией в РФ было не в 1990—1991 гг., как это следует из анализа графика по основной оси, а еще в 1978г., если изучать график по вспомогательной оси.

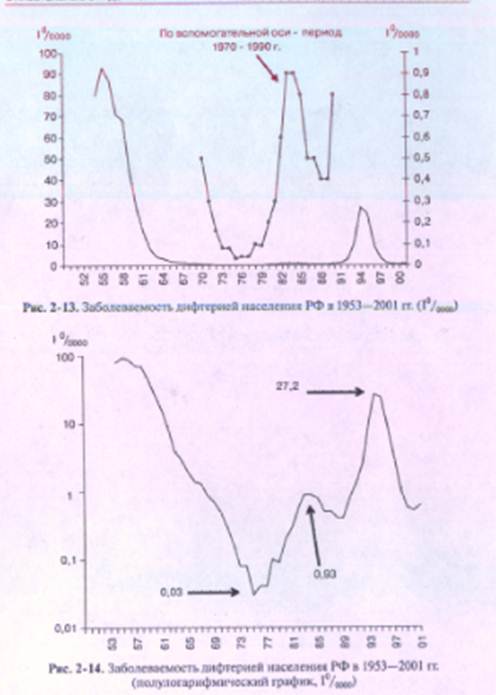
Возможный вариант отображения тех же данных — использование по­лулогарифмического графика. Однако внешний вид кривой на таком гра­фике (рис. 2-14) будет отличен от арифметического графика (см. рис. 2-13).

Для большей наглядности и точных выводов целесообразно (по воз­можности) на вертикальную ось диаграмм наносить цену деления в ин­тенсивных показателях и одновременно соответствующие им значения абсолютных чисел заболеваний так, как это сделано на рис. 2-15. На­несение числа заболевших (см. рис. 2-15) позволяет понять, какое ко­личество больных скрыто за незначительными интенсивными показа­телями заболеваемости брюшным тифом населения РФ в 1992—2001 гг.

Дополнительное нанесение на график числа заболевших особенно важно при необходимости изучить динамику заболеваемости отдельной, небольшой группы населения. В таких случаях за значительными интен­сивными показателями могут быть скрыты единичные случаи болезни. Не­знание этого может привести к ошибочным эпидемиологическим выводам.

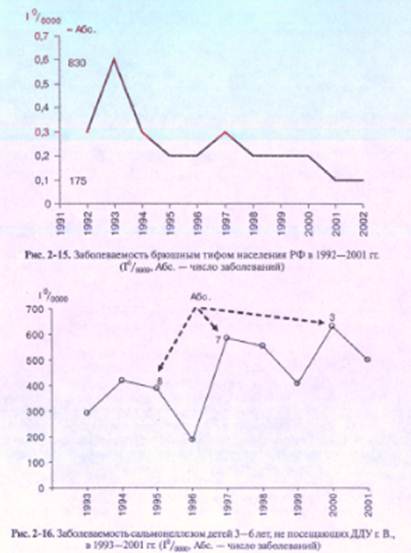
Единственное ограничение этого метода — существенное измене­ние численности населения в изучаемые годы. В таких случаях абсолют­ные числа заболевших можно нанести непосредственно рядом с кри­вой динамики интенсивных показателей (рис. 2-16). Данный способ дает возможность понять (см. рис, 2-16), что «устрашающие» показатели соответствуют максимум 8 случаям сальмонеллеза среди детей этой группы. На графике абсолютное число заболеваний в 2000 г. (3 случая) выше 8 случаев в 1994 г., поскольку было резкое (почти в 3 раза) сниже­ние численности детей, не посещающих ДДУ.

Полулогарифмические графики

При необходимости можно самостоятельно создать нестандартную логарифмическую шкалу с любой длиной основных разрядов. В стан­дартной шкале она составляет 10 см. Масштабная сетка полулогарифми­ческого графика представлена на рис. 2-17. Пересечение оси X и оси Y, в отличие от арифметического графика, происходит не в точке со значе­нием О, а в любой точке со значением 10" (10 в степени «n»), например 0,1 или 1,или 10 ит.д. При этом цена каждого следующего основного деле­ния обязательно возрастает в 10 раз.

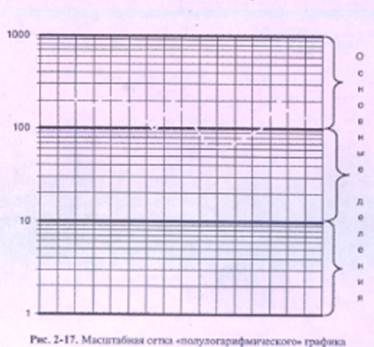
Выбор значения первого основного деления и их общее количество зависят от минимальных и максимальных показателей, которые необхо­димо отражать на диаграмме. Чаще всего число основных делений не пре­вышает четырех.

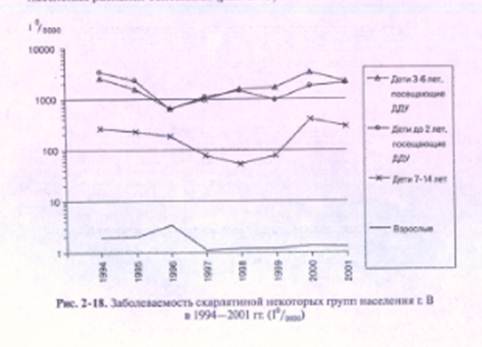
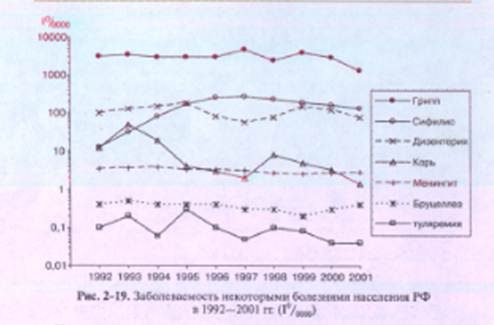
Основное предназначение полулогарифмического графика — разме­щение нескольких кривых заболеваемости, показатели которых отличны более чем в 10 раз. Особенно важно использовать такие диаграммы, когда показатели отдельных кривых различаются в 100 раз и более. В та­ких случаях один полулогарифмический график позволяет наглядно от­разить и сравнить, например, разные уровни заболеваемости какой-либо болезнью нескольких групп населения (рис. 2-18) или заболеваемость населения разными болезнями (рис. 2-19).

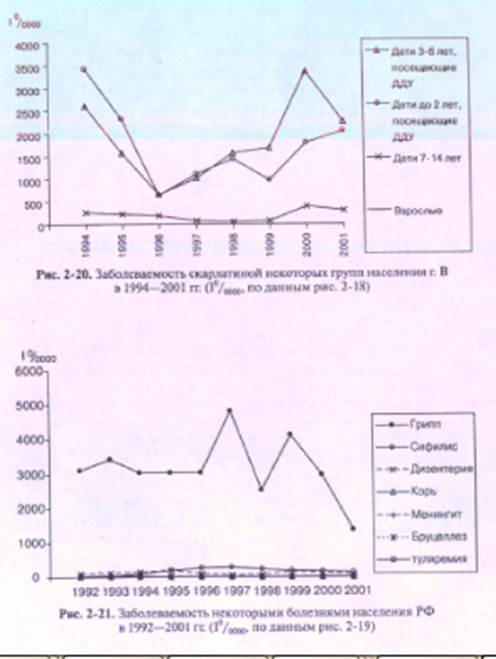
На арифметических графиках, в ситуациях существенного различия показателей разных кривых, сделать корректные выводы о каких либо особенностях соотношения и динамики показателей часто невозможно. Так, на рис. 2-20 не различима кривая заболеваемости взрослых, хотя этот график построен по уже используемым данным (см. рис. 2-18).

По рис. 2-21 можно оценить только динамику заболеваемости грип­пом, а обо всех остальных шести инфекциях — сказать, что уровень забо­леваемости ими существенно ниже, чем заболеваемость гриппом

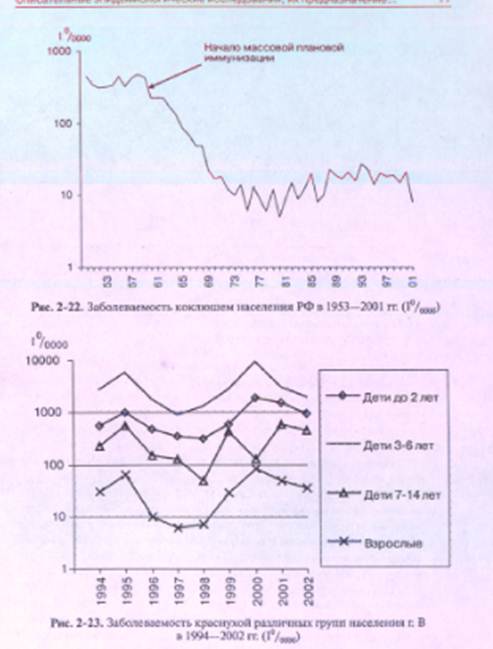
На полулогарифмическом графике может быть размещена и одна кри­вая с резко различающимися показателями в разные отрезки времени (рис. 2-22), хотя в этом случае более предпочтительны графики с исполь­зованием арифметической шкалы с дополнительной осью (см. рис. 2-12).

На оси У можно делать разрыв, если какие либо основные деления или их значительные части не востребованы при построении нескольких кривых.

При построении полулогарифмических графиков правило «золотого сечения» не несет существенного значения. Поэтому длину графика по оси X и оси У можно выбрать примерно одинаковой или, в пределах разумного, вытянуть по вертикальной или горизонтальной оси. Объясне­ние этого свойства полулогарифмических графиков проиллюстрировано на рисунках, построенных по одним данным (рис. 2-23, рис. 2-24).

Сравнение арифметических и полулогарифмических графиков

Отсутствие достаточного опыта и внимания при прочтении арифме­тических и полулогарифмических графиков создает почву для ошибоч­ных выводов об особенностях динамики, а, главным образом, об особен­ностях колебаний изучаемых показателей. Чаще всего ошибки допускают при оценке наличия (отсутствия) колебаний показателей одной кривой, отражающей периоды, резко различные по уровню заболеваемости. На­пример, периоды до и после введения плановой массовой иммунизации населения (см. рис. 2-22, рис. 2-25, рис. 2-26).

Выявляя и оценивая колебание показателей, важно помнить, что гра­фики в арифметической шкале наглядно и объективно отражают разницу колебаний показателей каждой кривой, т. е. насколько изменилась их вели­чина. И наоборот, графики в полулогарифмической шкале создают ложное визуальное представление того, насколько изменились колеблющиеся по­казатели заболеваемости, в то же время объективно отражают, во сколько раз снизилась (повысилась) заболеваемость в сравниваемые годы.

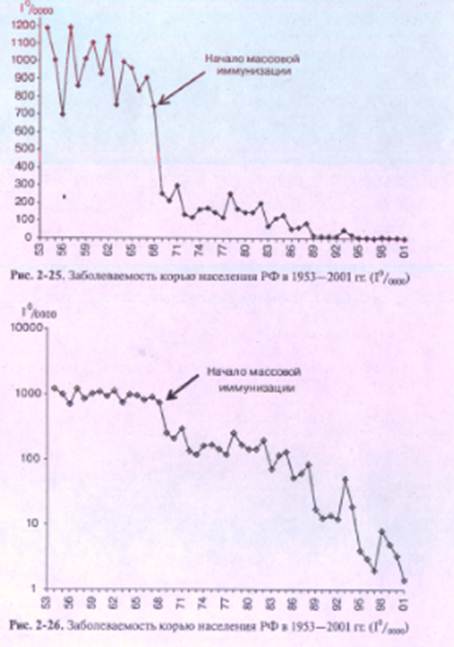
Именно из-за этого внешний вид кривой, построенной по одними тем же данным, на диаграммах с использованием арифметической и полулогариф­мической шкалы может сильно различаться, создавая впечатление, будто диаграммы отражают совершенно разные ситуации. Различия внешнего вида кривых будут тем больше, чем больше различия между максимальными и минимальными показателями по которым построена данная кривая (см. рис. 2-25, рис. 2-26). Это положение хорошо иллюстрирует сравнение двух приведенных ранее рисунков 2-12 (кривая по основной шкале) и 2-13. Соответственно разному внешнему виду графиков могут быть сделаны раз­ные и нередко ошибочные описательные выводы. Рассмотрим на примере.

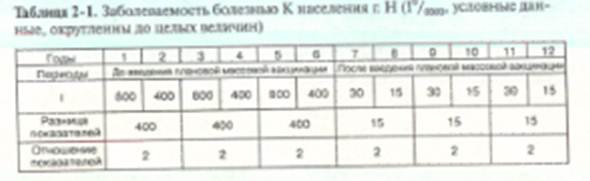
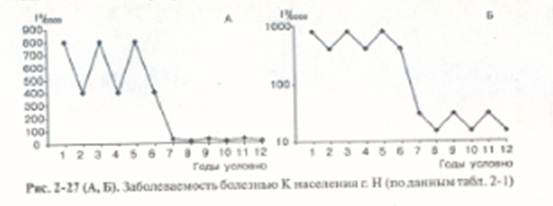
По данным табл. 2-1 разница сравниваемых показателей в разные пе­риоды существенна: 400 и 15°/оооо соответственно. Именно поэтому на арифметическом графике (рис. 2-27 А) отрезки кривых в первом и втором периодах имеют разную длину, и даже возникает впечатление, что во вто­ром периоде практически нет колебаний показателей.

Отношение сравниваемых показателей одинаково (2 раза), и поэтому, несмотря на выраженное абсолютное различие показателей в разные пери­оды, в тех же периодах отрезки кривых на полулогарифмическом графике имеют одинаковую длину (см. рис. 2-27 Б). Такой внешний вид графика может привести к совершенно другому выводу: несмотря на резкое снижение заболеваемости в двух сравниваемых периодах, отмечают однотипные колебания показателей заболеваемости болезнью К населения г. Н. Однако вы­вод «однотипные колебания» обязательно требует уточнения в том, что под однотипностью в данном случае понимают одинаковое отношение, а не раз­ницу показателей. В противном случае, по инерции, так как большинство проявлений оценивают по разности показателей, вывод «однотипные ко­лебания» может быть расценен как колебания с одинаковой амплитудой.

Другой пример.

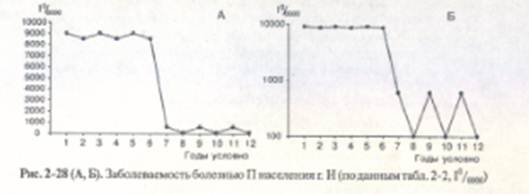
В отличии от данных табл. 2-1, в табл. 2-2 разница сравниваемых пока­зателей в двух периодах одинакова (500°/оооо), а отношение тех же показате­лей в этих периодах различается почти в 6 раз. Соответственно различается и внешний вид арифметического и полулогарифмического графиков.

Отрезки между сравниваемыми показателями в двух периодах имеют одинаковую длину, а это отражает одинаковую разницу показателей (рис. 2-28 А). Следовательно, можно сделать ориентировочный вывод: несмотря на резкое снижение заболеваемости идо, и после вакцинации, колебания заболеваемости полностью однотипны.

Отметим (рис. 2-28 Б), что внешний вид кривой настолько изменен, что это может привести к неверному выводу об отсутствии колебаний показателей до введения вакцинации и появлении выраженных колебаний показателей заболеваемости болезнью П населения г. Н в поствакцинальный период.

Еще сложнее анализ реальных данных одной кривой, когда в разные пе­риоды показатели заболеваемости резко различаются и, кроме того, в один из периодов отмечают тенденцию снижения (повышения) заболеваемости и постоянное изменение как разницы, так и отношения показателей.

При изучении полулогарифмических графиков, сравнивая длину отрезков кривой за одинаковые интервалы времени, по инерции (так как чаще используют арифметическую шкалу) ошибочно делают такие же выводы, как и по графикам в арифметической шкале. Однако и анализ арифметического графика, как было показано ранее, тоже может при­вести к некорректным выводам.

Какой же тип графиков использовать? Ответ: универсальных графи­ков, т. е. применимых для реализации всех целей анализа, не существует. Возможности арифметического и полулогарифмического графиков за­висят от целей и тех данных, которые предстоит отразить.

Арифметический график следует использовать, когда отсутствует су­щественное различие показателей заболеваемости одной или нескольких кривых. В таких случаях график корректно отражает особенности дина­мики и структуры показателей заболеваемости. В ситуациях существен­ного различия показателей, получению правильных выводов помогает введение дополнительной шкалы.

Полулогарифмический график незаменим, если необходимо на од­ном рисунке разместить несколько кривых, существенно различающихся по показателям заболеваемости. В таком случае один график позволяет наглядно отразить положение кривых заболеваемости относительно друг друга. Он же чаще всего помогает в таких случаях оценить синхронность (асинхронность) колебаний показателей нескольких кривых. Однако такой график не дает возможности правильно оценить наличие колебаний на от­дельных участках одной или нескольких кривых, построенных по резко различающимся (внутри каждой кривой) показателям заболеваемости. По­лулогарифмический график также незаменим, когда наглядно необходимо отобразить не разницу, а отношение показателей заболеваемости.

Столбиковые (столбчатые) диаграммы

Есть разные виды столбиковых диаграмм, но общая их черта — изобра­жение признака в виде плоского или объемного столбика. Как и графики, столбчатые диаграммы должны иметь вертикальную и горизонтальную ось с необходимыми обозначениями. Высота столбиков соответствует величине признака с учетом масштаба диаграммы. Ширина столбиков одной диаграммы должна быть одинаковой, а их расположение — чаще вертикальным, но может быть и горизонтальным.

В эпидемиологических исследованиях применяют две разновидности столбиковых диаграмм: гистограммы; дискретные диаграммы.

Дата добавления: 2014-09-29; просмотров: 1005; Нарушение авторских прав

Мы поможем в написании ваших работ!