Сферические резервуары

Сферические резервуары (рис. 52) предназначены для хранения сжиженных газов под высоким избыточным внутренним давлением от 0,25 до 2,0 МПа. Объем их колеблется от 600 до 4000 м³.

Рис. 52. Сферические резервуары для хранения сжиженных газов

Проектирование сферических резервуаров (рис. 53) выполняется с учетом требований СНиП 2.09.03 – 85 «Сооружение промышленных предприятий» и СНиП П-23-81 «Стальные конструкции». Выбор материалов зависит от температуры окружающей среды и температуры продукта.

Рис. 53. 3-D модель группы из четырех сферических резервуаров на фундаменте

Основным элементом конструкции сферического резервуара является оболочка, которую собирают из лепестков двоякой кривизны, а также купола и днища. Сферические резервуары более сложны в изготовлении, чем цилинд­рические, при этом трудоемкость их изготовления определяется, преж­де всего, принятой схемой раскроя сферы, которая чаще всего принимается экваториально-меридиональной или меридиональной (рис. 54).

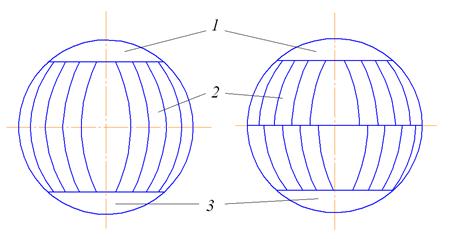
Рис. 54. Схемы раскроя сферического резервуара:

а) меридиональный; б) экваториально-меридиональный

1 – купол; 2 – лепестки; 3 - днище

Элементы оболочки (лепестки) толщиной до 36 мм вальцуют в холодном состоя­нии на шаровых вальцах, при большей толщине штампуют в горячем состоянии на прессах. Сначала лепестки соединяются на прихватках и образуют сферу. Затем их сваривают автоматами с помощью специаль­ных манипуляторов-вращателей (рис. 55), которые позволяют выполнять сварные швы в нижнем положении. Для крупных резервуаров (объемом 2 тыс. м³ и более) допускается монтаж сферических резервуаров без применения манипуляторов (рис. 56).

Рис. 55. Использование манипулятора-вращателя для сварки сферического резервуара

Рис. 56. Монтаж сферического резервуара

Сферические резервуары чаще всего опираются на систему стоек 5 (рис. 57), выполняемых из труб или двутавров и привариваемых к лепесткам оболочки. Такая конструкция опор обеспечивает достаточную свободу температурных деформаций оболочки. Число лепестков в экваториальном сечении должно быть кратным числу опорных стоек, а их ширина зависит от размеров стандартных листов.

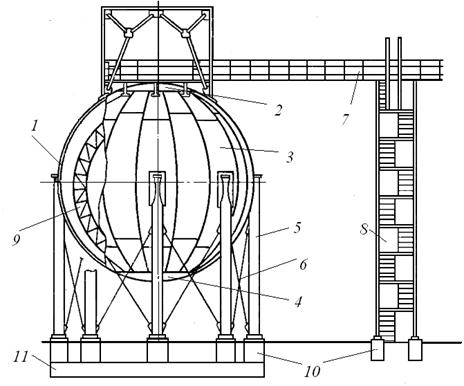
Рис. 57. Схема сферического резервуара

1 — сферическая оболочка резервуара; 2 — купол; 3 — лепестки оболочки; 4 — днище оболочки; 5 — стойки опоры; 6 — связи между опорами; 7 — го­ризонтальная площадка; 8 — шахтная лестница; 9 — внутренняя смотровая лестница; 10 — столбчатые фундаменты шахтной лестницы; 11 – кольцевой железобетонный фундамент

Для создания пространственной жесткости сооружения все колонны должны соединяться между собой крестовыми связями 6. Сферические резервуары для их обслуживания в процессе эксплуатации оборудуют площадками 7 с перилами и лестницами. Лестницы выполняют шахтного типа 8 или подвижными вокруг резервуара. Для осмотра оболочек внутри резервуара служат подвижные лестницы 9, доступ к которым возможен сверху и снизу резервуаров.

9.1. Определение напряжений в осесимметричных оболочках по безмоментной теории

Оболочками называют тела, толщина которых значительно меньше двух других измерений. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, называется срединной поверхностью. Если срединная поверхность образует часть сферы, конуса или цилиндра, оболочку соответственно называют сферической, конической или цилиндрической. Толщина оболочки может изменяться по какому-то закону или оставаться постоянной.

Осесимметричными оболочками называют такие, срединная поверхность которых представляет собой поверхность вращения, т.е. образуется в результате вращения плоской кривой вокруг прямой линии, называемой осью и лежащей в той же плоскости (рис. 58).

Задача о расчете оболочек вращения решаются значительно проще в том случае, когда можно принять, что напряжения в оболочке постоянны по толщине. Соответственно в этом случае будут отсутствовать изгибающие моменты. Теория, построенная на таком предположении, называется безмоментной теорией оболочек. Такие оболочки работают только на растяжение-сжатие и являются наиболее прочными и жесткими. В связи с этим при проектировании несущих оболочечных конструкций необходимо стремиться обеспечить их работу как безмоментных.

Рассмотрим осесимметричную оболочку толщиной 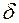(рис. 58). Обозначим через 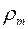радиус кривизны дуги меридиана срединной поверхности (рис. 58, а), а через 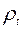второй главный радиус или радиус кривизны нормального сечения перпендикулярного к дуге меридиана. Этот радиус равен отрезку нормали между поверхностью оболочки и осью симметрии. В общем случае величина радиусов кривизны 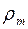и 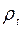является функцией угла 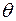между нормалью и осью симметрии.

Выделим на поверхности оболочки элемент с размерам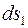и и 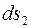двумя меридианальными и нормальными коническими сечениями (рис. 58, б).

На гранях этого элемента возникают напряжения и 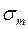(рис. 59, а). Напряжение называется окружным, а напряжение 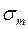меридианальным и его вектор направлен по дуге меридиана.

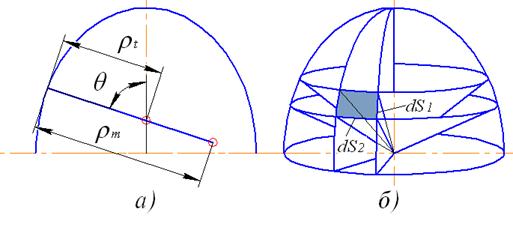
Рис. 58. Схема осесимметричной оболочки

Составим уравнение равновесия выделенного элемента. На его гранях возникают силы

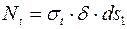и (9.1)

Внутреннее давление создает силу по нормали к элементу равную 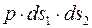. Составим сумму проекций этих сил на нормаль, не учитывая слагаемые второго порядка малости от напряжени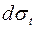й и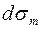

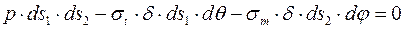. (9.2)

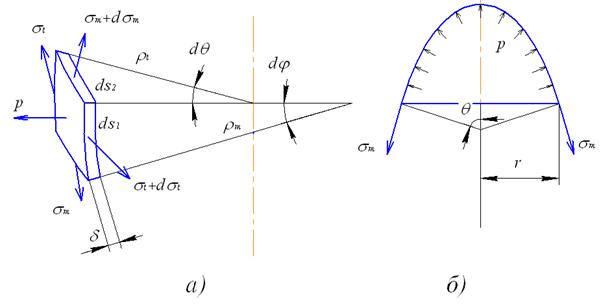
Рис. 59. Расчетная схема для определения напряжений в безмоментной оболочке

Учитывая геометрические соотношения

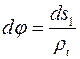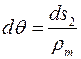; , (9.3)

окончательно получаем

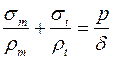. (9.4)

Это соотношение носит название уравнения Лапласа.

Так как в уравнение Лапласа входят два неизвестных напряжения, необходимо составить ещё одно уравнение проекций сил на направление оси оболочки. При этом удобнее составлять такое соотношение не для элемента, а для части оболочки, отсеченной коническим нормальным сечением (рис. 59, б). Для того, чтобы правильно использовать такое уравнение равновесия необходимо помнить следующую теорему.

Если на какую-то поверхность действует равномерно распределенное давление, то, независимо от формы этой поверхности, проекция равнодействующей сил давления на заданную ось равна произведению давления на площадь проекции поверхности на плоскость, перпендикулярную к заданной оси.

9.2. Определение толщины стенки оболочки сферического резервуара

При исследовании напряженно-деформированного состояния оболочки сферического резервуара необходимо учитывать, что её двоякая кривизна увеличивает сопротивление действию внутреннего давления. Это обстоятельство значительно увеличивает несущую способность конструкции и позволяет хранить легко испаряющиеся углеводороды при высоком давлении

Расчет на прочность оболочки сферического резервуара с целью определения толщины стенки оболочки производится для случая её нагружения избыточным давлением 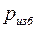(рис. 60). В сферической оболочке меридиональные 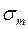и окружные напряжения связаны уравнением Лапласа (9.4). Для точки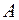

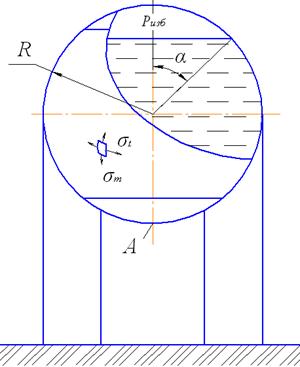
Рис. 60. Расчетная схема сферического резервуара

(рис. 60) они будут равны между собой, как и радиусы кривизны 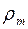и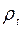

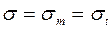
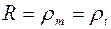. (9.5)

С учетом этого получаем

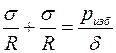
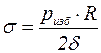(9.6)

Для этого случая условие прочности будет иметь следующий вид

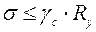, (9.7)

где – коэффициент условий работы;

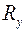– расчетное сопротивление материала оболочки.

Из условия прочности вытекает формула для вычисления толщины стенки сферического резервуара

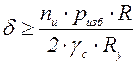, (9.8)

где 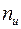– коэффициент надежности для ибыточного давления.

С учетом вытяжки заготовок при вальцовке необходимо толщину листа для криволинейных элементов стенки оболочки увеличивать на 2 – 3 мм.

Для точки 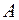(рис. 60) легко вычислить напряжения с учетом гидростатического давления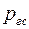

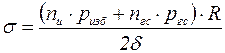
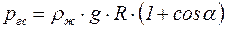, (9.9)

где 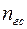– коэффициент надежности для гидростатического давления;

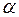– угол, определяющий высоту налива жидкой фазы углеводорода в сферическом резервуаре;

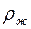– плотность жидкого углеводорода.

Избыточное давление в сферическом резервуаре является величиной переменной и определяется давлением упругости насыщенных паров 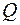, которое зависит от состава углеводоров, количества продукта в резервуаре и температуры.

9.3. Кратковременные нагрузки на сферический резервуар

Расчетная весовая нагрузка снегового покрова на сферический резервуар

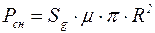, (9.10)

где 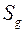– расчетное значение веса снегового покрова на 1 м² горизонтальной поверхности земли;

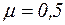- коэффициент перехода от веса снегового покрова земли к снеговой нагрузке на покрытие сферического резервуара.

Статическая составляющая ветрового давления

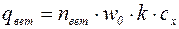, (9.11)

где 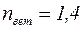– коэффициент надежности по ветровой нагрузке;

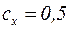– коэффициент лобового сопротивления сферической оболочки;

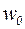– нормативное значение ветрового давления;

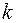– коэффициент, учитывающий изменение ветрового давления по высоте.

Суммарная ветровая нагрузка на сферический резервуар

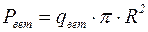. (9.12)

9.4. Деформации сферической оболочки

Радиальное перемещение оболочки 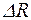от избыточного давления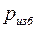

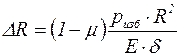, (9.13)

где 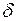– толщина стенки сферического резервуара;

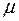– коэффициент Пуассона.

Радиальное перемещение оболочки 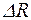от перепада температуры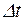

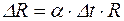, (9.14)

где 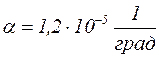– температурный коэффициент линейного расширения.

9.5. Расчет оболочки на устойчивость

Оболочку сферического резервуара необходимо рассчитать на устойчивость для случая возникновения в резервуаре абсолютного вакуума равного 0,1 МПа.

Чтобы стенка резервуара не потеряла устойчивость от возникновения вакуума 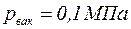, должно выполняться следующее условие. Сжимающие напряжения 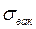в стенке сферической оболочки от воздействия вакуума не должны превышать критических напряжений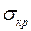

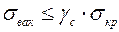, (9.15)

,

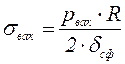где 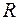– радиус сферической оболочки;

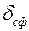– толщина стенки оболочки.

Критические напряжения для сферических оболочек с соотношением размеров 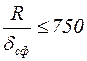вычисляются в соответствии со СНиП II-23-81 «Стальные конструкции»

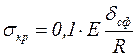. (9.16)

9.6. Расчет стоек резервуара

Расчет стоек резервуара проводится по методике, которая изложена выше для внецентренно сжатых колонн.

Стойки сферических резервуаров работают на внецентренное сжатие (рис.я) и поэтому должны рассчитываться на прочность и на устойчивость.

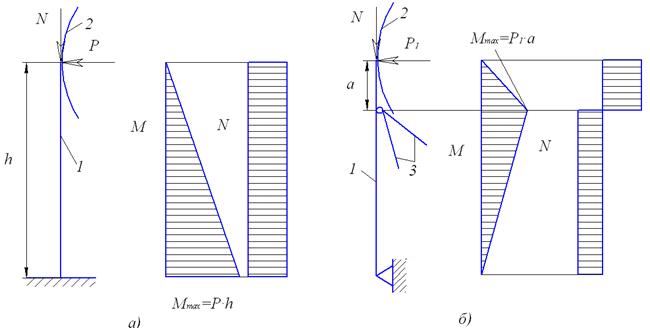
Рис. 61. Расчетные схемы стойки сферического резервуара

1) – стойка; 2) – оболочка; 3) – связи между опорами

Продольная сила на стойку 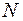определяется с учетом всех нагрузок 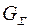, действующих на стойку

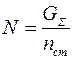, (9.17)

где 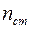– число стоек.

Максимальная суммарная расчетная нагрузка 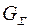должна вычисляться для варианта нагружения при проведении испытаний путем полного заполнения сферической оболочки водой

, (9.18)

где 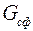– вес стальной сферической оболочки; 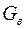– вес воды;

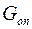– вес опор и связей; 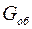– вес оборудования;

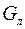– снеговая нагрузка; – вес лестниц, площадок и т.п.;

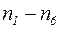– коэффициенты надежности по нагрузке.

Величина эксцентриситета 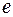определяется максимальным моментом, который возникает в стойке от поперечной силы 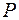или 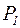(рис. 61), которые могут появляться при радиальной деформации сферической оболочки или от ветровой нагрузки

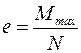. (9.19)

Дата добавления: 2014-10-02; просмотров: 1452; Нарушение авторских прав

Мы поможем в написании ваших работ!