ОПРЕДЕЛЕНИЕ ОПТИЧЕСКИХ СВОЙСТВ МИНЕРАЛОВ ПРИ ДВУХ СКРЕЩЕННЫХ НИКОЛЯХ В ПАРАЛЛЕЛЬНОМ СВЕТЕ

Цель. Освоение методики и приобретение практических навыков микроскопического определения минералов горных пород при скрещенных николях в параллельном свете. Данная работа направлена на формирование компетенции ПК-11 и ОК-9, т.е. подготовить студентов к выбору технических средств для решения общепрофессиональных задач и научиться осуществлять контроль за их применением, развить стремление к саморазвитию и повышению своей квалификации и мастерства.

Организационная форма занятия. Интерактивная форма проведения занятия – разбор конкретных ситуаций.

Указания по технике безопасности смотреть в приложении 1.

Методические рекомендации

Теоретическое обоснование. При двух николях определяется: сила двойного лучепреломления; угол погасания и оптическая ориентировка минерала (наименование осей оптической индикатрисы); состав плагиоклазов.

Для того чтобы понимать явления, наблюдаемые в минерале при скрещенных николях, необходимо ясно представлять себе особенности прохождения света через систему поляризатор – кристалл – анализатор.

Рассмотрим минерал кубической сингонии или сечения, перпендикулярного к оптической оси анизотропного минерала. В том и другом случае имеем дело с изотропной средой, пропускающей световые волны, колеблющиеся в любых направлениях, следовательно, наблюдаемые явления ничем не будут отличаться от системы двух скрещенных николей. Плоскополяризованная волна, выйдя из поляризатора, пройдет через изотропную среду, сохранив плоскость колебаний без изменения, анализатором пропущена не будет, и поле зрения микроскопа останется темным при любых поворотах столика микроскопа.

Если же между николями поместить анизотропную пластинку, то возникнут явления, существенно отличающиеся от вышеописанных. Как уже известно, анизотропное сечение минерала пропускает световые волны только в двух взаимно перпендикулярных направлениях, соответствующих направлениям осей эллиптического сечения индикатрисы, лежащего в плоскости исследуемого разреза.

Если поворотом столика микроскопа минерал поставить так, чтобы оси его индикатрисы совпали с плоскостями колебаний нижнего и верхнего николей, то волны, вышедшие из нижнего николя – поляризатора, беспрепятственно пройдут через минерал, сохраняя приобретенные в поляризаторе колебания, и далее верхним николем – анализатором пропущены не будут. При повороте столика микроскопа на 360° оси эллиптического сечения индикатрисы четыре раза совпадут с плоскостями колебаний в николях и, следовательно, четыре раза минерал будет на погасании.

При условии косого положения осей индикатрисы исследуемого сечения минерала относительно плоскостей колебаний поляризатора и анализатора плоскополяризованная волна с амплитудой k, приобретенной в поляризаторе, войдя в минерал, разложится по правилу параллелограмма на две взаимно перпендикулярные волны с амплитудами k₁ и k₂, колеблющиеся в направлении осей эллиптического сечения индикатрисы n_g и n_p. Скорость колебаний каждой волны обратно пропорциональна показателям преломления соответствующих направлений. При прохождении через минерал волна, колеблющаяся в направлении оси n_p и поэтому имеющая большую скорость, обгонит волну колеблющуюся в направлении n_g с меньшей скоростью, на некоторую величину R, называемою разностью хода.

Выйдя из минерала, обе плоскополяризованные волны будут перемещаться с одинаковыми скоростями, сохраняя разность хода и направления колебаний, которые они приобрели в кристалле.

Проходя через верхний николь (анализатор) под углом к плоскости его колебаний, каждая из волн вновь разложится на две.

Таким образом, верхний николь в системе поляризатор – кристалл – анализатор не только позволяет отличать изотропный минерал от анизотропного, но и создает условия, необходимые для интерференции.

Сила двойного лучепреломления минералов. Луч света, проходящий через пластинку анизотропного минерала (кристаллы средних и низших сингоний), разлагается на два луча с разными показателями преломления, распространяющимися с различными скоростями, и колеблющимися во взаимно-перпендикулярных плоскостях. Это явление получило название двойного лучепреломления.

Силой двойного лучепреломления (D) называется величина, показывающая насколько показатель преломления одного луча отличается от показателя преломления другого:

D= n ₁- n₂ , (1)

где n₁ и n₂ – величины показателей преломления.

Сила двойного лучепреломления – величина переменная. Она изменяется от 0, когда луч направлен по оптической оси кристалла, до какого-то максимума, когда луч направлен перпендикулярно к оптической оси (в одноосных кристаллах) или к плоскости оптических осей (в двуосных кристаллах). За истинную величину силы двойного лучепреломления (ведь только она может использоваться для определения минерала) принимают ее максимальное значение:

D = n_g - n_p , (2)

где n_g – наибольший по величине показатель преломления данного минерала, а n_p – наименьший.

Определение силы двойного лучепреломления минералов основано на изучении явления интерференции световых волн, проходящих через кристалл в шлифе.

Луч света, входя в кристалл, раздваивается и каждая из образовавшихся световых волн распространяется в кристалле со своей скоростью. В результате один луч обгоняет другой, и между ними возникает разность хода (R). Величина разности хода измеряется в миллимикронах и прямо пропорциональна длине пути, пройденного в анизотропной среде, то есть толщине кристаллической пластинки – (толщина шлифа) и силе двойного лучепреломления данного кристалла – D:

R = d D = d(n_g - n_p) (3)

Наличие определенной разности хода при прохождении лучей света через анализатор обусловливает их интерференцию, вследствие чего зерна минералов при изучении их под микроскопом в белом свете приобретают интерференционные окраски. При этом каждому значению разности хода соответствует своя интерференционная окраска. Следовательно, по характеру интерференционной окраски можно определить разность хода – R, которая, в свою очередь, связана с искомой уже известной зависимостью (3). В конечном итоге, определение силы двойного лучепреломления минерала сводится к определению интерференционной окраски.

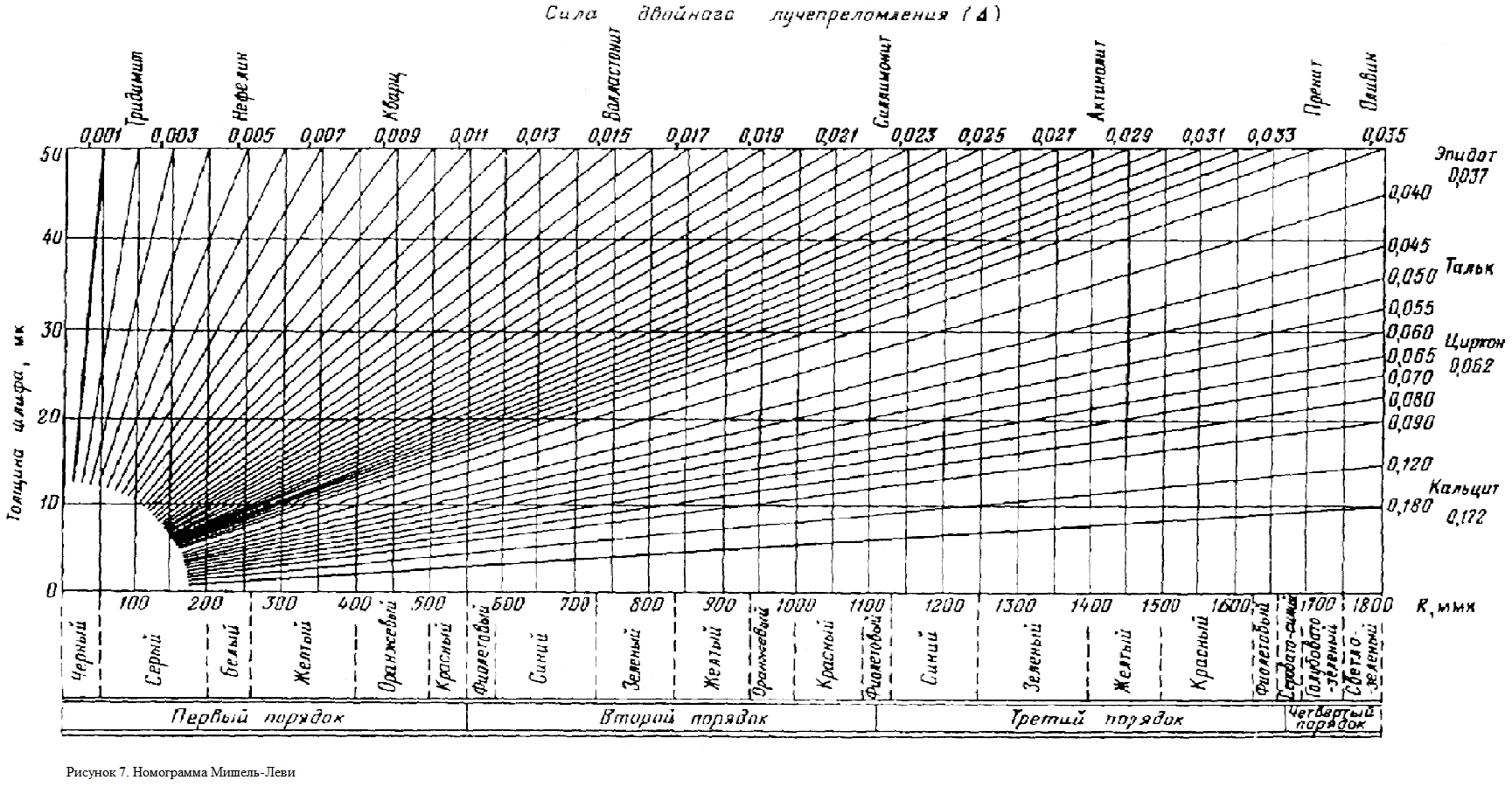
При определении силы двойного лучепреломления минералов пользуются таблицей Мишель-Леви, которая является графическим выражением зависимости (3).

По горизонтальной оси этой таблицы нанесены величины разности хода (в миллимикронах) с соответствующей им интерференционной окраской (в виде вертикальных полосок соответствующих цветов) (рис. 7).

При увеличении R цвета периодически повторяются. Это позволяет разбить их на порядки.

В первый порядок входят цвета: серый, белый, желтый, оранжевый и красный, постепенно переходящие друг в друга. Второй и третий порядки начинаются с фиолетового цвета, далее следуют синий, зеленый, желтый, оранжевый и красный.

В первом порядке имеются отсутствующие в других порядках серый и белый цвета, но нет синего и зеленого. В первом и втором порядках оттенки цветов выражены наиболее резко. Дальше окраски постепенно бледнеют, и при очень больших разностях хода они сливаются и образуют интерференционную окраску высшего порядка.

По вертикальной оси таблицы отложена толщина шлифов (в сотых и тысячных долях мм). Из нижнего левого угла таблицы веерообразно вверх и вправо расходятся прямые линии, на концах которых указаны значения силы двойного лучепреломления.

Для практического определения силы двойного лучепреломления необходимо под микроскопом найти наивысшую интерференционную окраску минерала и точку пересечения ее на таблице Мишель-Леви с горизонтальной линией, соответствующей стандартной толщине шлифа = 0,03 мм. Через эту точку проходит одна из веерообразно расходящихся линий, на верхнем конце которой и указана искомая величина = n_g - n_p .

При изучении интерференционной окраски минерала необходимо определить ее порядок. Для этого пользуются так называемым правилом каемок и методом компенсации.

Определение силы двойного лучепреломления по краевым каемкам в зернах.

Весьма часто зерна минералов утончаются к краям, в то время как значительно большая площадь зерна имеет плоскую поверхность, параллельную нижней поверхности зерна.

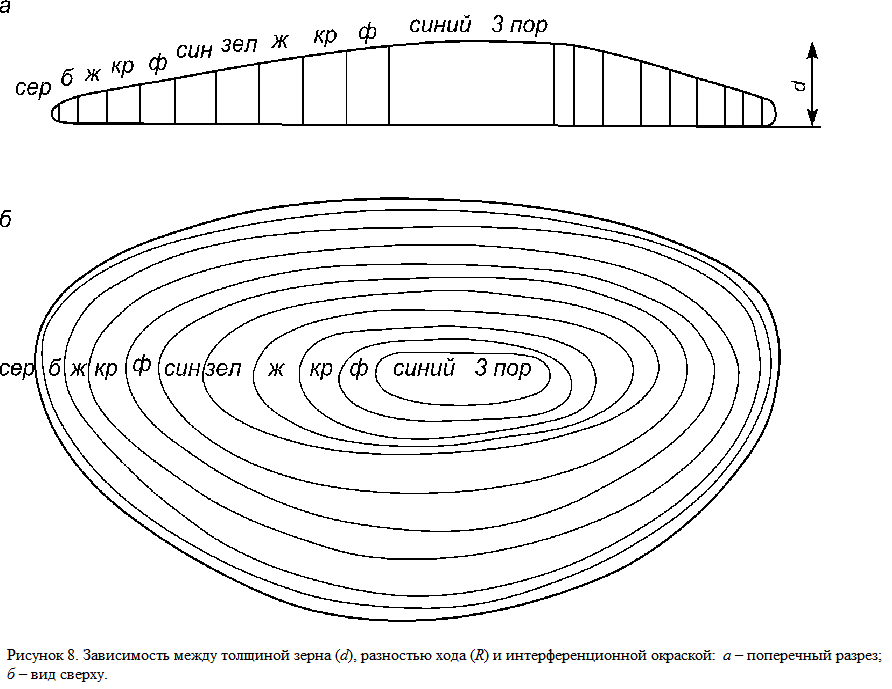
В зависимости от этого интерференционная окраска зерна понижается к самым краям зерна, на которых наблюдаются различия в интерференционных окрасках, так что нередко можно различать цвета первых порядков (рис. 8).

Наблюдая от края к центру зерна полоски интерференционных цветов, заканчивающиеся красным цветом, можно подсчитать, сколько красных полосок сменяют друг друга в направлении от края к его центру и, следовательно, выяснить, к какому порядку относится интерференционная окраска зерна в его центральной части (количество красных каемок плюс единица). Затем необходимо использовать номограмму Мишель-Леви для определения силы двойного лучепреломления [1].

Ввиду того, что краевые каемки очень узки, наблюдения над ними проводятся обычно через объективы с большим увеличением (чаще 20х; 40х).

Аппаратура, оборудование и материалы. Микроскопы с объективами и окулярами различного увеличения, набор шлифов.

Порядок выполнения работы

Методика и порядок определение силы двойного лучепреломления по краевым каемкам в зернах

1. Отрегулировать микроскоп (освещение, центрировка).

2. Включить анализатор и проверить скрещенность николей.

3. Поставить на столик шлиф и просмотреть все зерна (с включенным анализатором). Сравнивая их интерференционную окраску с окрасками номограммы Мишель-Леви, выбрать зерно с наивысшей интерференционной окраской.

4. Поставить объектив с большим увеличением, подсчитать количество красных каемок и определить порядок интерференционной окраски (количество красных каемок + 1).

5. Пользуясь номограммой Мишель-Леви, определить силу двойного лучепреломления минерала.

Определение силы двойного лучепреломления при помощи компенсатора.

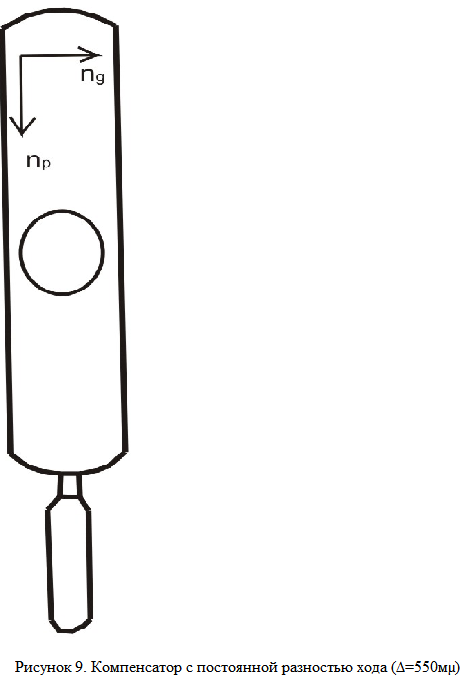
Компенсатор представляет собой прибор, изготовленный из кристаллов кварца и гипса. В том случае, когда он имеет постоянную разность хода около 550 миллимикрон, что соответствует собственной интерференционной окраске кварца или гипса – красной первого порядка, то его называют кварцевой пластинкой (рис. 9).

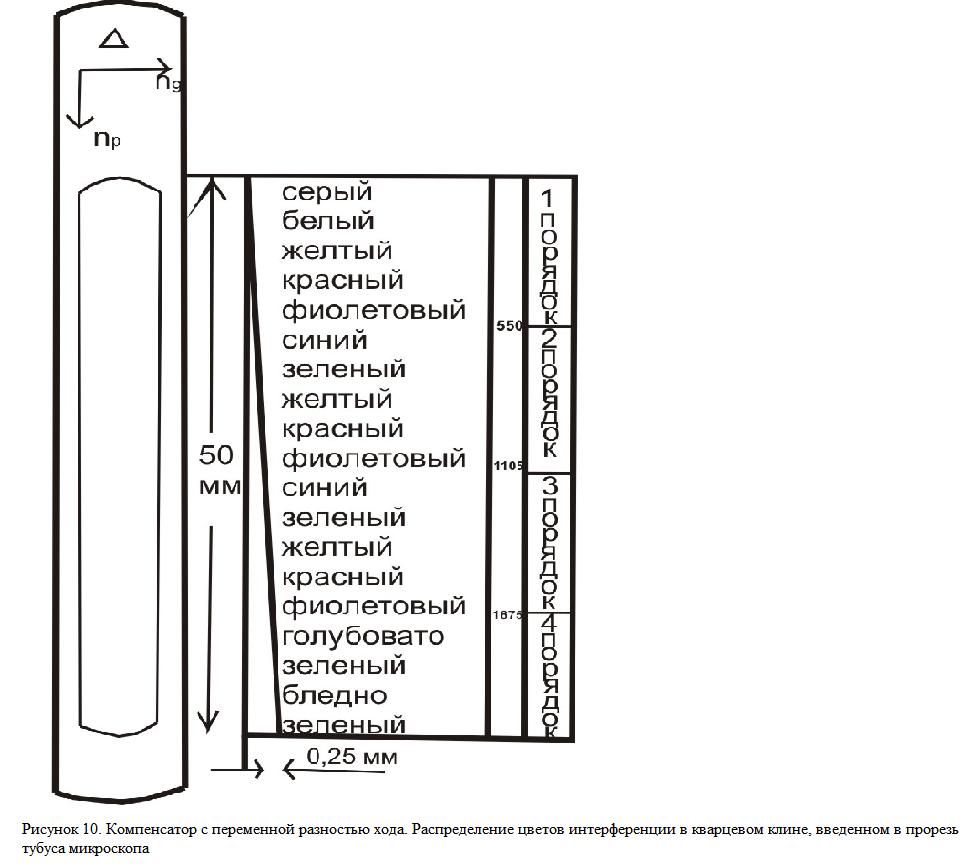
Компенсатор, называемый кварцевым клином, представляет в поперечном разрезе пластинку в форме тонкого клина (рис. 10). Его разность хода переменная. На оправе указана его оптическая ориентировка, обычно сходная с той, которая указана для гипсовой и кварцевой пластинок (т.е. N_g соответствует короткой, а N_p - длинной стороне оправы).

При вдвигании кварцевого клина в прорезь тубуса микроскопа изменяются последовательно интерференционные цвета от начала 1 порядка до 4 порядка.

При определении силы двойного лучепреломления используется правило компенсации.

Известно, что разность хода в кристаллическом зерне возрастает пропорционально длине пути, проходимого световыми волнами в этом зерне.

Поэтому, если на пути распространения света, над кристаллическим зерном поместить другую кристаллическую пластинку (в данном случае компенсатор) таким образом, чтобы направления одноименных осей оптических индикатрис зерна и компенсатора совпадали, то результирующая разность хода будет равна сумме разностей хода зерна и компенсатора (т.е. она увеличится), что вызовет повышение интерференционной окраски.

Если поместить компенсатор таким образом, что будут совпадать разноименные оси оптических индикатрис зерна и компенсатора, то суммарная разность хода будет равна разности разностей хода зерна и компенсатора, что приведет к уменьшению порядка интерференционной окраски.

Если разность хода компенсатора будет равна разности хода в исследуемом зерне минерала, то в итоге общая разность хода световых волн будет равна нулю или, как принято говорить, произойдет компенсация разности хода в зерне, а зерно приобретет серую интерференционную окраску первого порядка [2].

Методика и порядок определения силы двойного лучепреломления при помощи компенсатора.

1. Поставьте исследуемое зерно поворотом предметного столика в положение угасания, при котором направления колебаний в зерне совпадают с главными сечениями николей.

2. От положения, соответствующего угасанию, предметный столик микроскопа поверните на 45^о по часовой стрелке или против ее вращения.

3. Вдвигайте кварцевый клин до тех пор, пока не будет достигнута компенсация разности хода в зерне (появление темно-серой окраски в центре поля зерна).

4. Если компенсация не достигается при данном положении исследуемого зерна, то поверните предметный столик на 90° (до этого компенсатор удалите из поля зрения). Поворотом на 90° будет достигнута замена положения осей оптической индикатрисы (т.е., на место n_g помещается n_p и наоборот). Снова вдвигайте кварцевый клин до достижения компенсации.

5. Удалите из центра поля зрения зерно, сдвигая его в сторону так, чтобы на его месте был участок, занятый изотропным веществом канадского бальзама.

Если компенсация была достигнута полностью, то на этом участке будет та же самая интерференционная окраска, которая была у исследуемого зерна.

6. Медленно выдвигайте из тубуса кварцевый клин и наблюдайте, сколько раз через центр поля зрения пройдут полоски красного цвета, граничные для порядков интерференционных окрасок. Это позволит установить, к какому порядку следует отнести интерференционную окраску исследуемого минерала, а затем, пользуясь номограммой Мишель-Леви, определить силу двойного лучепреломления.

Определение угла погасания и оптической ориентировки минерала.

Определить оптическую ориентировку означает найти положение осей индикатрисы n_g и n_p относительно кристаллографических осей (X,Y,Z).

Кристаллографические оси совпадают с трещинами спайности, с удлинением зерна или направлением прямолинейных граней.

Практически определение оптической ориентировки сводится к замеру угла между осью индикатрисы и спайностью, или удлинением зерна, который получил название угла погасания. Угол погасания замеряется в разрезе, параллельном плоскости индикатрисы (или плоскости оптических осей). Этот разрез характеризуется наивысшей для данного минерала интерференционной окраской.

Как известно, спайность наблюдается в виде системы параллельных трещин. Положение же осей оптической индикатрисы может быть определено в момент погасания зерна при изучении его в скрещенных николях. Кристаллы погасают, то есть становятся темными тогда, когда направления осей индикатрисы кристалла совпадают с направлением световых колебаний в николях – поляризаторе и анализаторе. При полном повороте столика микроскопа совпадение направлений колебаний в кристалле и в николях, а, следовательно, и погасание происходит четыре раза, через каждые 90⁰.

В отрегулированном микроскопе николи установлены так, что плоскости колебаний пропускаемых ими световых лучей ориентированы параллельно нитям окуляра. Следовательно, нити окуляра в момент погасания зерна указывают на положение осей его индикатрисы.

Для измерения угла погасания берут отсчеты по лимбу столика микроскопа при двух его положениях. Первый отсчет берут тогда, когда направление трещин спайности параллельно одной из нитей окуляра.

Второй отсчет производят в момент погасания зерна, когда параллельно нитям окуляра располагаются оси индикатрисы минерала.

Оси индикатрисы в кристаллах средних сингоний, ромбической сингонии и некоторых разрезах моноклинной сингонии совпадают с кристаллографическими осями, то есть спайностью. Угол погасания в таких кристаллах будет равен 0. Такой тип погасания получил название прямого погасания.

В большинстве разрезов кристаллов моноклинной сингонии и в кристаллах триклинной сингонии оси индикатрисы не совпадают с кристаллографическими осями, то есть спайностью. Угол погасания в этом случае не равен 0, а тип погасания называется косым погасанием.

Помимо положения осей индикатрисы, в кристалле, для определения оптической ориентировки необходимо знать их наименование, то есть определить, какая из них является осью n_g, а какая n_p. Для этого используют компенсатор. Обычно применяют кварцевый компенсатор с постоянной разностью хода в 550 миллимикрон.

Если при введении компенсатора в оптическую систему микроскопа оси индикатрисы в нем и в зерне минерала совпадают по направлению и наименованию, то в соответствии с правилом компенсации разность хода компенсатора прибавляется к разности хода минерала, вследствие чего интерференционная окраска зерна повышается на 550 миллимикрон. В случае совпадения разноименных осей индикатрисы, разность хода компенсатора вычитается из разности хода минерала (или наоборот), и интерференционная окраска зерна понижается [4].

Методика и порядок определения угла погасания и оптической ориентировки минерала

1. Отрегулируйте микроскоп (освещение, центрировка, скрещенность николей).

2. Установите нити окуляра параллельно плоскости колебаний поляризатора и анализатора, используя характер плеохроизма биотита. Для этого, выключив анализатор, поставьте в точку пересечения нитей окуляра зерно биотита с хорошо выраженными трещинами спайности. Затем поверните столик микроскопа до наиболее темной окраски биотита. В этот момент одна из нитей окуляра должна быть параллельна его спайности.

Если этого не наблюдается, следует повернуть окуляр так, чтобы нить совпала с направлением трещин спайности.

3. Поставьте на столик микроскопа шлиф с исследуемым минералом и, включив анализатор, найдите зерно с четкими трещинами спайности и наиболее высокой интерференционной окраской (в этом сечении лежат оси n_g и n_p).

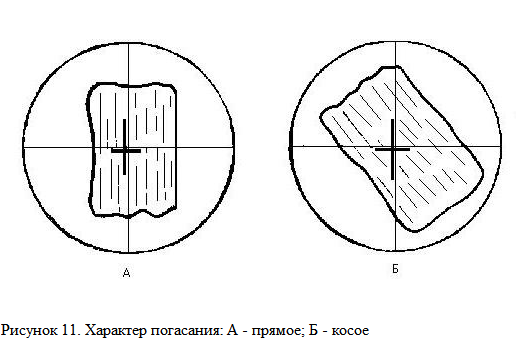
4. Поставьте зерно в центр поля зрения. Поверните столик микроскопа до момента, когда трещины спайности будут параллельны нити окуляра. Введите анализатор. Зерно погасло – погасание прямое (рис. 11А). Если зерно не погасло – косое (рис. 11Б). В таком положении сделайте первый отсчет по лимбу столика.

5. Поверните столик микроскопа до полного погасания зерна и сделайте второй отсчет. Разница отсчетов соответствует величине угла погасания.

6. Зарисуйте зерно в момент угасания, нанесите положение осей индикатрисы (параллельно нитям окуляра) и укажите на рисунке величину измеренного угла погасания. Чтобы лучше видеть спайность, зарисовку можно сделать с выключенным анализатором.

7. Из положения погасания поверните столик микроскопа по часовой стрелке на 45⁰ (для совмещения осей индикатрисы минерала с осями индикатрисы компенсатора).

8. Введите компенсатор в специальную прорезь в тубусе микроскопа, расположенную над объективом, и наблюдайте за изменением интерференционной окраски зерна минерала.

В случае ее повышения – в кристалле и компенсаторе совпадают одноименные оси индикатрис и, следовательно, ось индикатрисы минерала, параллельная горизонтальной нити окуляра, является ось – n_р, в случае же понижения интерференционной окраски – осью n_g (рис. 12).

9. Подпишите на зарисовке наименование осей индикатрисы.

10. Определите знак удлинения минерала. Удлинение минерала считается положительным, если ближайшей осью индикатрисы по отношению к длинной стороне кристалла или направлению спайности является ось n_g и отрицательным, если этой осью является n_p.

Знак удлинения определяется в том случае, если угловое расстояние между осью индикатрисы и осью удлинения меньше 45⁰. Если минерал обладает ясно выраженным удлинением, но угловое расстояние между длинной его стороной и ближайшей осью индикатрисы равно 45⁰, знак удлинения считается нейтральным. В качестве минералов с нейтральным знаком удлинения можно назвать некоторые моноклинные пироксены (авгит, диопсид).

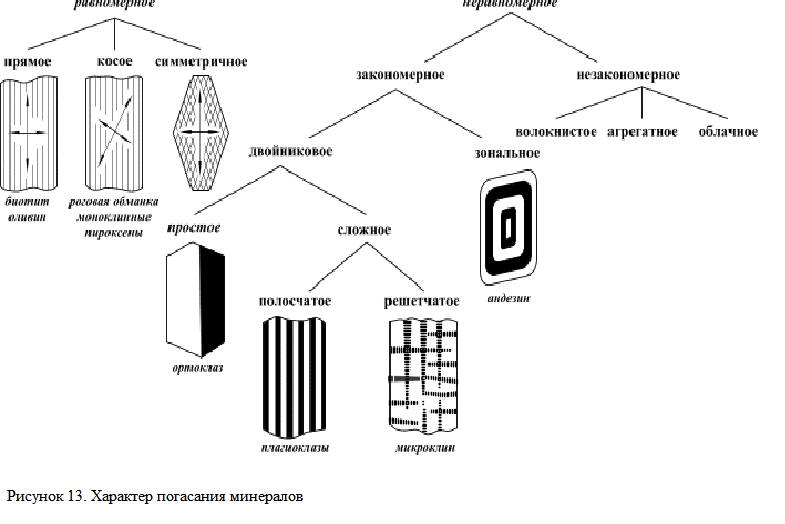
11. Найдите и зарисуйте минералы, обладающие различными типами погасания, пользуясь, рисунком 13.

Содержание отчета, форма и правила оформления отчета о выполненной работе. В отчете следует отразить цель работы, краткие теоретические предпосылки, описать методику изучения различных оптических свойств минералов, определяемых при двух николях, зарисовать все операции.

При защите работы студент должен иметь отчет о выполненной работе, уметь ответить на предложенные преподавателем вопросы и самостоятельно определить оптические свойства минералов в контрольном шлифе.

Вопросы для защиты

1. Какие оптические свойства минералов изучаются при двух скрещенных николях в параллельном свете?

2. Что такое двупреломление?

3. В каких разрезах проявляется двупреломление?

4. Как определить силу двупреломления?

5. Как пользоваться номограммой Мишель-Леви?

6. Зарисуйте ход лучей через систему поляризатор – кристалл – анализатор.

7. Что такое компенсатор и какие типы компенсаторов Вы знаете?

8. С какими направлениями в кристалле совпадает кристаллографическая ось?

9. Какое погасание называется прямым? Косым?

10. Охарактеризуйте типы погасаний минералов.

Дата добавления: 2014-10-08; просмотров: 1178; Нарушение авторских прав

Мы поможем в написании ваших работ!