Постоянный шаг аргумента

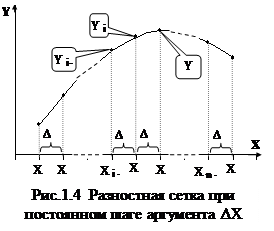Для заданных табулированных функций, когда аргументы представляются арифметической прогрессией (шаг аргумента постоянен), существуют легко реализуемые в таблицах Excel расчетные формулы численного интегрирования и дифференцирования, основанные на использовании разностных подходов.

Для численного дифференцирования используют прямые разности на шаге ΔX (вариант 1) или центральные разности на двух шагах ΔX (вариант 2):

вариант 1 - ;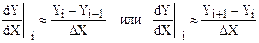

вариант 2 - 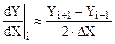. (1.28)

Наиболее просто численное интегрирование проводится методом трапеций. На интервале равном шагу интегрирования:

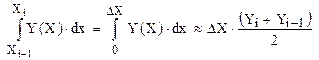(1.29)

Интеграл на интервале [X ₁, X _n] определяется как:

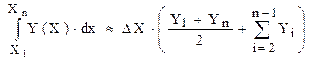(1.30)

При численном интегрировании более точным считается метод Симпсона. В этом случае на интервале [X _i-1, X _i+1] (два смежных шага ΔX) функция описывается полиномом второго порядка, а интеграл определяется по зависимости:

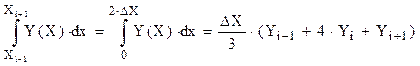(1.31)

Интеграл на интервале [X ₁, X _n] определяется как сумма интегралов на отдельных интервалах [X _i-1, X _i+1] расположенных с шагом 2ΔX:

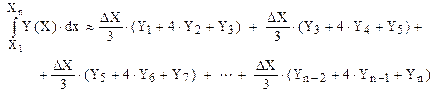(1.32)

где n – нечетное число.

Дата добавления: 2014-10-10; просмотров: 284; Нарушение авторских прав

Мы поможем в написании ваших работ!