Переменный шаг аргумента

Когда аргументы представлены не арифметической прогрессией формулы для численного интегрирования и дифференцирования усложняются.

Одношаговые формулы дифференцирования и интегрирования принимают вид:

¾ дифференцирование (вариант 1):

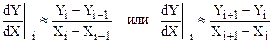(1.33)

¾ интегрирование методом трапеций на интервале [X _i-1, X _i]:

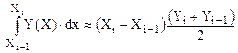(1.34)

Интеграл на интервале [X ₁, X _n] определяется как сумма интегралов на отдельных интервалах [X _i-1, X _i]:

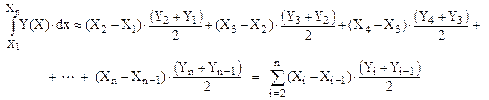(1.35)

Для двухшаговых схем численного дифференцирования и интегрирования используется аппроксимацию заданной табулированной функции на интервале [X _i-1, X _i+1] полиномом второго порядка:

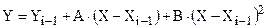(1.36)

где ,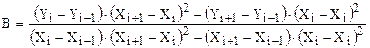

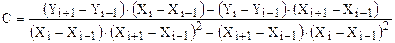
Тогда численное значение первой производной для i-ой точки равно:

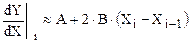(1.37)

Численное значение интеграла на интервале [X _i-1, X _i+1] получим по зависимости:

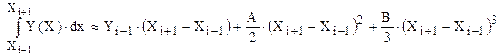(1.38)

Интеграл на интервале [X ₁, X _n] определяется как сумма интегралов на отдельных интервалах [X _i-1, X _i].

Дата добавления: 2014-10-10; просмотров: 265; Нарушение авторских прав

Мы поможем в написании ваших работ!