Параллельное соединение r, L, C

На рисунке 3.19. приведена электрическая схема с параллельно соединенными элементами r, L, C и к цепи приложено напряжение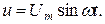

Проводимости каждой ветви соответственно равны:

.

Эти формулы имеют ограниченное применение, т.е. они справедливы в том случае, если ветвь содержит один идеальный элемент.

Согласно первому закону Кирхгофа общий ток равен:

.

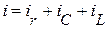Оценку соотношений между действующими значениями токов в каждой ветви электрической цепи можно оценить с помощью векторной диаграммы, изображенной на рисунке 3.20.

Порядок построения векторной диаграммы следующий.

1. Откладываем вектор напряжения в произвольном направлении.

2. Далее откладываем токи в каждой из параллельных ветвей:

2.1. Ток на резистивном элементе 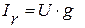совпадает по направлению с напряжением .

2.2. Ток на индуктивном элементе отстает по направлению от напряжения на 90⁰.

2.3. Ток на емкостном элементе опережает по направлению напряжение на 90⁰.

3. Результирующий вектор тока 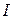, получаем путем векторного сложения 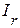, , 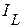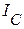(начало вектора 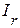соединяем с концом вектора ).

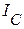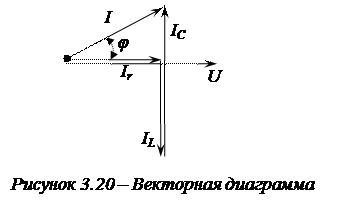На приведенной векторной диаграмме ток опережает напряжение на угол j, следовательно, режим работы активно-емкостной.

Из векторной диаграммы следует:

,

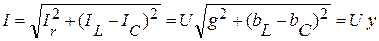где 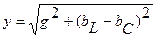– полная проводимость цепи.

Выражение I =Uу представляет закон Ома для цепи синусоидального тока.

Соотношения между величинами активной 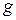, реактивной и полной проводимостями можно оценить с помощью треугольника проводимостей (рис. 3.21).

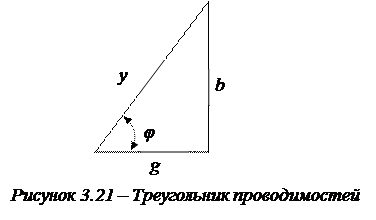
Из этого треугольника следует:

.

Цепь с произвольным числом параллельно соединенных идеальных элементов, по аналогии, обладает следующими свойствами. Однородные параллельно соединенные элементы можно заменить эквивалентными и тогда:

g = å g_i ;

b_L = å b_Li ;

b_C = å b_Ci .

Таким образом, параллельно соединённые одноименные сопротивления можно заменить эквивалентными.

В общем случае, при параллельном соединении резистивного, индуктивного и емкостного элементов, ток в неразветвленном участке цепи, можно разбить на две составляющие тока активную 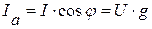и реактивную 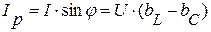(рис. 3.22).

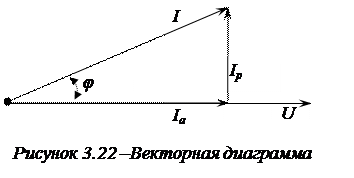Из векторной диаграммы следует: .

Пример 3.2. Возможные варианты расчета цепей с параллельным соединением, рассмотрим на примере электрической цепи, представленной на рисунке 3.23. Заданы величины U = 150 (B), ω = 314 (рад/с) (f = 50 Гц), r₁ = 22 (Ом), r₂ = 17 (Ом), r₃ = 14 (Ом), L₁ = 60 (мГн), С₂ = 300 (мкФ), L₃ = 30 (мГн). Необходимо определить токи в ветвях I_i и ток в неразветвленном участке цепи I.

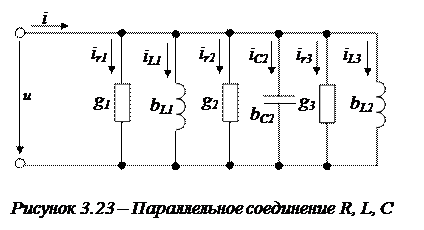1. Определяем омические сопротивления реактивных элементов:

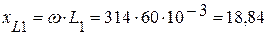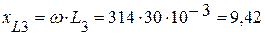(Ом),

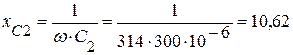(Ом),

(Ом).

2. Определяем полную проводимость цепи.

2.1. Проводимость ветвей с резистивными элементами

(См),

(См),

(См).

Эквивалентная проводимость ветвей с резистивными элементами

(См).

2.2. Проводимости ветвей с индуктивными элементами

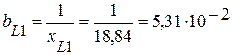(См),

(См).

Эквивалентная проводимость ветвей с индуктивными элементами

(См).

2.3. Проводимость ветви с емкостным элементом

(См).

Эквивалентная проводимость ветвей с емкостным элементом

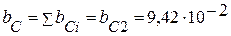(См).

2.4. Полная проводимость

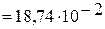(См).

3. Определяем ток в цепи (А).

4. Определяем токи в каждой параллельной ветви

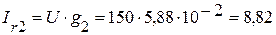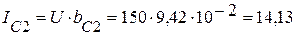(А),

(А),

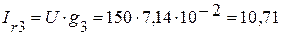(А),

(А),

(А),

(А).

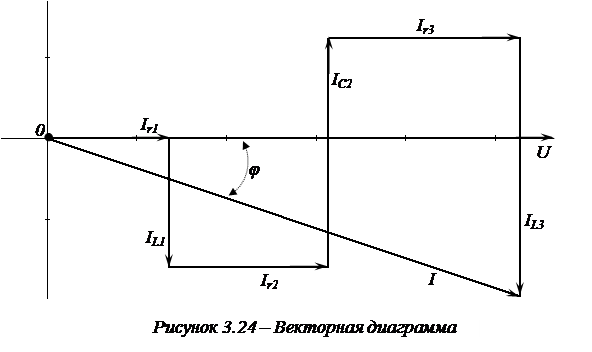
7. Векторная диаграмма рассматриваемой цепи приведена на рисунке 3.24.

Дата добавления: 2014-02-27; просмотров: 1264; Нарушение авторских прав

Мы поможем в написании ваших работ!