
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выпуклость и вогнутость
|
Читайте также: |
Пусть функция 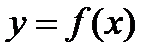 дифференцируема в любой точке интервала (a, b). Тогда существует касательная к графику функции в любой точке графика.
дифференцируема в любой точке интервала (a, b). Тогда существует касательная к графику функции в любой точке графика.
Определение 4. Непрерывная функция 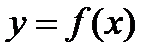 называется выпуклой вниз (т.е. вогнутой) (рис.3), если все точки кривой лежат выше любой ее касательной к графику
называется выпуклой вниз (т.е. вогнутой) (рис.3), если все точки кривой лежат выше любой ее касательной к графику 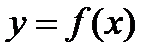 на интервале (a, b). И называется выпуклой вверх (рис.4), если все точки кривой лежат ниже этих касательных.
на интервале (a, b). И называется выпуклой вверх (рис.4), если все точки кривой лежат ниже этих касательных.
| у |
| х |
| х |
| у |
| а |
| а |
| b |
| b |
| О |
| О |
Рис.3 Рис.4
Теорема 4.
Если функция 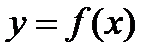 имеет на интервале (a, b) конечную вторую производную
имеет на интервале (a, b) конечную вторую производную 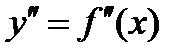 и
и 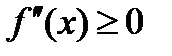 во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вниз (вогнут). Если
во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вниз (вогнут). Если 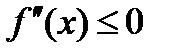 во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вверх.
во всех точках х интервала (a, b), то график данной функции имеет выпуклость, направленную вверх.
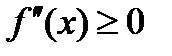
|
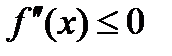
|
Определение 5. Точки, при переходе через которые функция меняет направление выпуклости, называются точками перегиба функции 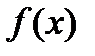 .
.
Определение 6. Точка 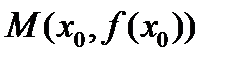 называется точкой перегиба графика функции
называется точкой перегиба графика функции 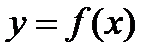 , если существует такая окрестность точки
, если существует такая окрестность точки 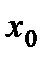 , в пределах которой график функции слева и справа от точки х0 имеет разные направления выпуклости.
, в пределах которой график функции слева и справа от точки х0 имеет разные направления выпуклости.
Теорема 5. (необходимое условие существования точки перегиба).
Если функция 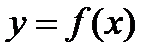 дважды дифференцируема в точке
дважды дифференцируема в точке 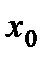 , непрерывна в этой точке, и ее график имеет перегиб в точке
, непрерывна в этой точке, и ее график имеет перегиб в точке 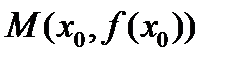 , тогда
, тогда 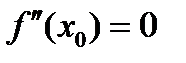 .
.
Теорема 6. (достаточное условие существования точки перегиба).
Пусть функция 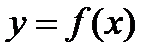 имеет вторую производную
имеет вторую производную 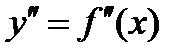 в некоторой окрестности точки
в некоторой окрестности точки 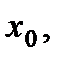 и пусть
и пусть 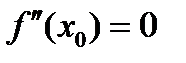 , либо
, либо 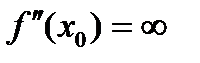 , либо
, либо 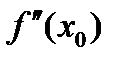 не существует, тогда, если в пределах указанной окрестности вторая производная
не существует, тогда, если в пределах указанной окрестности вторая производная 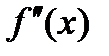 имеет разные знаки слева и справа от точки х0, то график функции имеет перегиб в точке
имеет разные знаки слева и справа от точки х0, то график функции имеет перегиб в точке 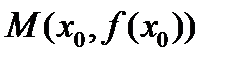 .
.
Замечание. Точка разрыва не является точкой перегиба, хотя при переходе через нее кривая зачастую меняет направление выпуклости.
5. Асимптоты
Определение 7. Прямая 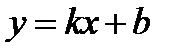 называется асимптотой для кривой
называется асимптотой для кривой 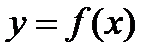 , если расстояние от точки М, лежащей на кривой, до прямой стремится к нулю при удалении точки М от начала координат в бесконечность.
, если расстояние от точки М, лежащей на кривой, до прямой стремится к нулю при удалении точки М от начала координат в бесконечность.
Существует три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 8. Прямая 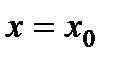 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 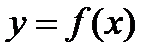 , если выполнено хотя бы одно из условий:
, если выполнено хотя бы одно из условий:
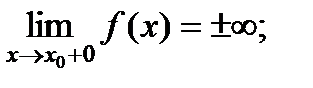
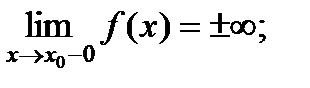
т.е. точка 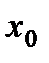 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Определение 9. Прямая 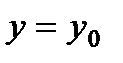 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 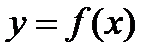 , если
, если 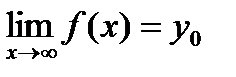 .
.
Определение 10. Прямая 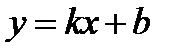 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 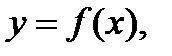 если существуют числа k и b такие, что
если существуют числа k и b такие, что
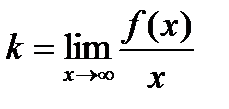 ,
, 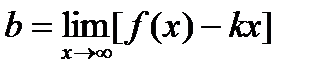 .
.
Замечание. Если оба предела существуют и конечны (т.е. равны числам), причем 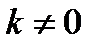 , то существует и наклонная асимптота. Если k = 0, то получим горизонтальную асимптоту. Если
, то существует и наклонная асимптота. Если k = 0, то получим горизонтальную асимптоту. Если 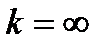 или
или 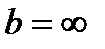 , то наклонных асимптот не существует.
, то наклонных асимптот не существует.
6. План исследования графика функции
1. Найти область определения функции.
2. Найти область непрерывности функции и точки разрыва. Определить характер точек разрыва.
3. Найти нули функции (точки пересечения с координатными осями).
4. Установить, не является ли график функции симметричным относительно какой-нибудь прямой (или координатной оси) или точки, т.е. проверить, является функция четной, или нечетной, или ни той и ни другой.
5. Проверить функцию на периодичность.
6. Найти промежутки монотонности и экстремумы.
7. Найти промежутки выпуклости и точки перегиба.
8. Найти асимптоты.
9. Найти несколько дополнительных значений функции.
10. Построить график.
| <== предыдущая страница | | | следующая страница ==> |
| Исследование функций с помощью производных | | | Шумовой режим застройки |
Дата добавления: 2014-11-01; просмотров: 489; Нарушение авторских прав

Мы поможем в написании ваших работ!