
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Исследование функций с помощью производных
1. Возрастание и убывание функций
Теорема 1.
Если во всех точках х некоторого промежутка D производная функции  , то функция
, то функция 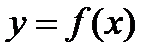 постоянна на этом промежутке.
постоянна на этом промежутке.
Доказательство
Функция  удовлетворяет всем условиям теоремы Лагранжа, т.е. для любых точек
удовлетворяет всем условиям теоремы Лагранжа, т.е. для любых точек  из промежутка D существует точка
из промежутка D существует точка  такая, что справедлива формула конечных приращений Лагранжа:
такая, что справедлива формула конечных приращений Лагранжа:  . По условию теоремы
. По условию теоремы  , следовательно,
, следовательно,  . Отсюда
. Отсюда  . Это означает, что функция
. Это означает, что функция 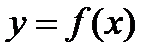 постоянна на этом промежутке, что и требовалось доказать.
постоянна на этом промежутке, что и требовалось доказать.
Теорема 2.
Для того чтобы дифференцируемая на интервале (a, b) функция  была возрастающей, необходимо и достаточно, чтобы выполнялось условие
была возрастающей, необходимо и достаточно, чтобы выполнялось условие
 (1)
(1)
Аналогично условие

является необходимым и достаточным для убывания функции  на интервале (a, b).
на интервале (a, b).
Доказательство
Необходимость
Пусть  – произвольная точка интервала (a, b). Из определения возрастающей функции имеем:
– произвольная точка интервала (a, b). Из определения возрастающей функции имеем:





Достаточность
Пусть выполняется условие (1) и 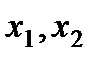 - произвольные точки из промежутка (a, b), причем
- произвольные точки из промежутка (a, b), причем  . Тогда по теореме Лагранжа существует точка
. Тогда по теореме Лагранжа существует точка  такая, что справедлива формула конечных приращений Лагранжа:
такая, что справедлива формула конечных приращений Лагранжа:
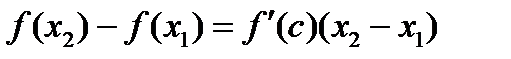 .
.
По условию теоремы 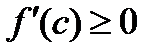 и
и  , следовательно,
, следовательно,  . Отсюда,
. Отсюда,  , т.е. функция не убывает, что и требовалось доказать.
, т.е. функция не убывает, что и требовалось доказать.
Определение 1. Промежутки возрастания и убывания называются промежутками монотонности.
| х |
| у |
| а |
| b |
| О |
| х |
| у |
| а |
| b |
| О |
S FfR8ls0isoGQH2WkpUctK6kLOk/DGtQVyHhpqhjimVTDGStR5sBOIGSgxvdlH6cxjsmBuhKqW+TL wqBd/Gt4aMB+oaRD3RbUfd4yKyhRrw1yfj6eToPQozGdnWVo2FNPeephhiNUQT0lw3Hl4+cIfBi4 xNnUMvL2UMmhZtRjpPPwd4LgT+0Y9fDDl38AAAD//wMAUEsDBBQABgAIAAAAIQBegqh23gAAAAkB AAAPAAAAZHJzL2Rvd25yZXYueG1sTI9BTsMwEEX3SNzBGiQ2iDo1aUNDJhUggdi29ACT2E0iYjuK 3Sa9PcOKLkfz9P/7xXa2vTibMXTeISwXCQjjaq871yAcvj8en0GESE5T751BuJgA2/L2pqBc+8nt zHkfG8EhLuSE0MY45FKGujWWwsIPxvHv6EdLkc+xkXqkicNtL1WSrKWlznFDS4N5b039sz9ZhOPX 9LDaTNVnPGS7dP1GXVb5C+L93fz6AiKaOf7D8KfP6lCyU+VPTgfRIzylyYZRBLVUIBhIkxWPqxAy pUCWhbxeUP4CAAD//wMAUEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAA AAAAAFtDb250ZW50X1R5cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAA AAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQSwECLQAUAAYACAAAACEAHAIBtjsCAAApBAAADgAAAAAA AAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAXoKodt4AAAAJAQAADwAA AAAAAAAAAAAAAACVBAAAZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAKAFAAAAAA== " stroked="f">
| α |
| α |

|

|
Рис.1 Рис.2
Геометрический смысл: если  то угол α – тупой (рис.1), если
то угол α – тупой (рис.1), если  то угол α – острый (рис.2).
то угол α – острый (рис.2).
2. Экстремумы.
пределение 2. Точка, отделяющая промежуток возрастания от промежутка убывания и наоборот, называется точкой экстремума.
Определение 3. Пусть функция 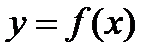 определена на [a, b]. Точка
определена на [a, b]. Точка  называется точкой максимума функции
называется точкой максимума функции 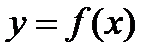 , если для любого х из некоторой достаточно малой окрестности точки
, если для любого х из некоторой достаточно малой окрестности точки 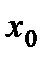 выполняется неравенство
выполняется неравенство 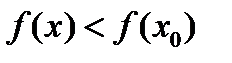 . Точка
. Точка  называется точкой минимума функции
называется точкой минимума функции 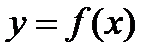 , если для любого х из некоторой достаточно малой окрестности точки
, если для любого х из некоторой достаточно малой окрестности точки 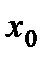 выполняется неравенство
выполняется неравенство  .
.
Точки максимума и минимума называются точками экстремума.
Теорема 2. (Необходимое условие существования экстремума).
Если функция 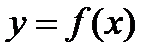 дифференцируема в точке
дифференцируема в точке 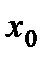 и имеет в этой точке экстремум, то
и имеет в этой точке экстремум, то
 .
.
Точки, в которых производная равна нулю, называются стационарными, а точки, в которых производная равна нулю или терпит разрыв, называются критическими. Все точки экстремума функции находятся среди ее критических точек.
Теорема 3. (Достаточное условие существования экстремума).
Если при переходе через критическую точку 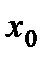 производная меняет знак
производная меняет знак
1) с «+» на «–», то 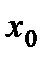 – точка максимума,
– точка максимума,
2) с «–» на «+», то 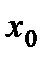 – точка минимума,
– точка минимума,
3) если не меняет знак, то в критической точке экстремума нет.
3. Наибольшее и наименьшее значение функции на отрезке.
1) находят на 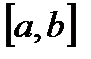 экстремумы;
экстремумы;
2) определяют значения 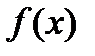 на концах
на концах 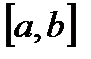 ;
;
3) из всех полученных значений выбирают наибольшее и наименьшее.
Практические задачи: транспортная задача о перевозке груза с минимальными затратами, задача об организации производственного процесса с целью получения максимальной прибыли и другие задачи, связанные с поиском оптимального решения, приводят к развитию и усовершенствованию методов отыскания наибольших и наименьших значений. Решением таких задач занимается особый раздел математики – линейное программирование.
| <== предыдущая страница | | | следующая страница ==> |
| Нормативные документы по метрологии | | | Выпуклость и вогнутость |
Дата добавления: 2014-11-01; просмотров: 395; Нарушение авторских прав

Мы поможем в написании ваших работ!