Частотные характеристики последовательного контура

Зависимости параметров цепи от частоты () называют частотными характеристиками, а зависимости действующих или амплитудных значений тока и напряжения от частоты – резонансными кривыми (), или амплитудно-частотными характеристиками.

Рассмотрим частотные характеристики пассивных элементов z(w), x(w), x_L(w), x_C(w). Для их оценки принимаем во внимание, что 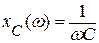, и . На рисунке 3.74, изображены частотные характеристики.

Проанализируем частотные характеристики:

1. При 0<w<w_о– полное сопротивление имеет емкостной характер.

2. При w = w_о– полное сопротивление имеет активный характер (резонанс).

3. При w_о<w< ¥– полное сопротивление имеет индуктивный характер.

Рассмотрим амплитудно-частотную характеристику I(w).

Для оценки I(w), воспользуемся выражением

.

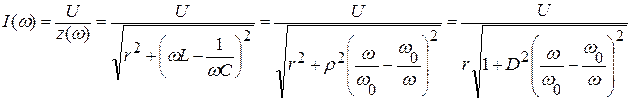Зависимость выражения представлена на рисунке 3.75.

Проанализируем частотные характеристики:

1. При w = 0 – I = 0 , так как при w → 0 х_С →∞ z→∞.

2. При 0 <w<w_о – по мере увеличения частоты реактивное сопротивление х_С уменьшается, следовательно, полное реактивное сопротивление х уменьшается, полное сопротивление z уменьшается и ток I возрастает

(x_C ¯ Þ x ¯ Þ z ¯ Þ I ­ ).

3. При w = w_о– полное сопротивление минимальное z = r, следовательно, значение тока наибольшее: .

4. При w >w_о – по мере уменьшения частоты (при x_L > x_C и при увеличении w) полное реактивное сопротивление х увеличивается, полное сопротивление z увеличивается и ток I убывает

(w > w_о x_L > x_C и если w ­, то x ­ Þ z ­ Þ I ¯ ).

5. Если w ® ¥, то I ® 0.

Оценим влияние добротности на форму кривой I(w).

При r = const Þ при всех добротностях. По мере увеличения добротности, график имеет более выраженный пик, т.е. перепад тока максимален.

На рисунке 3.76 приведены графики I(w) при различных добротностях (D₁ > D₂ > D₃).

Рассмотрим амплитудно-частотные характеристики U_L(w), U_C(w).

Для оценки U_L(w), воспользуемся выражением

Для оценки U_С(w), воспользуемся выражением

Зависимости выражений U_L(w) и U_C(w), представлены на рисунке 3.77.

Проанализируем амплитудно-частотную характеристику U_L(w):

1. При w = 0 сопротивление x_L = 0, ток I = 0, и следовательно U_L = 0.

2. При изменении частоты 0 до w₀ сопротивление x_L увеличивается и ток I увеличивается, и следовательно U_L возрастает.

3. При дальнейшем увеличении частоты w > w₀, ток I уменьшается, но при за счет роста x_L напряжение U_L продолжает возрастать.

4. При частоте w = w_L – кривая U_L (w)имеет максимум(U_L = U_max). Для определения w_L и U_L(w) необходимо взять производную. Тогда имеем , .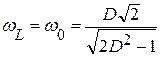

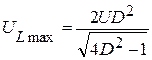5. При дальнейшем увеличении w ® ¥ – U_L ® U, т.е. стремится к напряжению на зажимах сети.

Проанализируем амплитудно-частотную характеристику U_С(w):

1. При w = 0 ток I в цепи отсутствует, и следовательно U_С = U.

2. При изменении частоты 0 до w₀ сопротивление x_С уменьшается и ток I увеличивается, и следовательно U_С возрастает.

3. При частоте w = w_С кривая U_С (w)имеет максимум(U_С = U_max). Для определения w_С и U_С(w) необходимо взять производную. Тогда имеем , 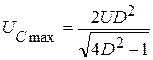. Следовательно, .

4. При w ® ¥ – U_С ® 0, т.к. ток I и x_С равны нулю.

Возможен случай, когда кривые U_L (w)и U_C (w)не будут иметь экстремума. Это будет следовать из выражения w_L иw_С.

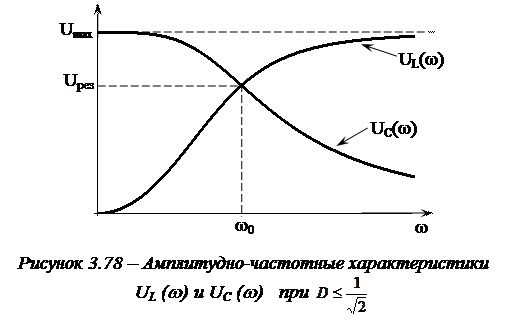
Если добротность w_L иw_С не являются действительными числами и на графике максимум отсутствует, а сами графики имеют монотонный характер, представленный на рисунке 3.78.

Дата добавления: 2014-02-27; просмотров: 372; Нарушение авторских прав

Мы поможем в написании ваших работ!