
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
При обработке результатов измерений по методу наименьших квадратов минимизируется сумма квадратов отклонений экспериментальных точек от искомой кривой. Причем развит метод только для случая линейных зависимостей. На первый взгляд может показаться, что область применимости этого метода значительно сужена. Однако это не так, поскольку многие нелинейные зависимости допускают линеаризацию, а применение метода наименьших квадратов к линеаризованным зависимостям значительно упрощает выкладки. Два примера были рассмотрены выше (при рассмотрении полулогарифмических и логарифмических масштабов). Приведем еще несколько зависимостей, допускающих линеаризацию.
1. 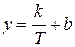 , где k и b – некоторые постоянные. Заменяя 1/T = x, т. е. откладывая по оси абсцисс обратные значения температуры, получим прямую:
, где k и b – некоторые постоянные. Заменяя 1/T = x, т. е. откладывая по оси абсцисс обратные значения температуры, получим прямую:
y = k x + b. (19)
2. y = a bx, где a и b – некоторые постоянные. Логарифмируем это уравнение: ln y = x ln b + ln a. Откладывая по оси ординат z = ln y (полулогарифмический масштаб), вновь получим прямую:
z = x ln b + ln a. (20)
3. 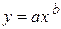 , где a и b – некоторые постоянные. Логарифмируя, получим
, где a и b – некоторые постоянные. Логарифмируя, получим 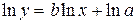 . Откладывая по оси ординат z =ln y, а по оси абсцисс t =ln x (логарифмический масштаб), вновь получим прямую:
. Откладывая по оси ординат z =ln y, а по оси абсцисс t =ln x (логарифмический масштаб), вновь получим прямую:
z = b t + ln a. (21)
Следует, однако, сказать, что общего рецепта линеаризации не существует, и в каждом конкретном случае следует искать свой подход.
Рассмотрим вывод рабочих формул (31) и (32) для расчета коэффициентов a и b. Пусть уравнение прямой дано в координатах y и x:
y = a x + b. (22)
Коэффициенты уравнения a и b надлежит выбрать наилучшим образом. Прямая будет наилучшей, если сумма квадратов всех отклонений экспериментальных точек от искомой прямой
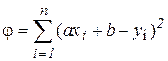 (23)
(23)
будет иметь наименьшее значение. Тогда из условия минимума:
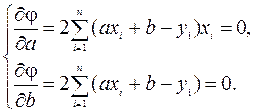 (24)
(24)
Из второго уравнения системы получим:
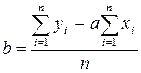 . (25)
. (25)
Подставим (25) в первое уравнение системы (24) и получим:
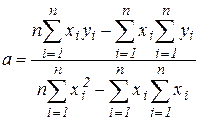 . (26)
. (26)
Необходимо ввести средние значения в соответствии с общими правилами:
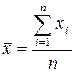 ;
; 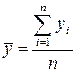 , (27)
, (27)
и отклонения от средних:
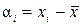 и
и 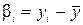 , (28)
, (28)
обладающих тем свойством, что
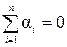 и
и 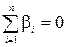 . (29)
. (29)
Покажем это на примере 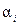 . Для этого просуммируем обе части первого равенства (28) по всем значениям i и разделим обе части этого равенства на число точек, тогда имеем:
. Для этого просуммируем обе части первого равенства (28) по всем значениям i и разделим обе части этого равенства на число точек, тогда имеем:
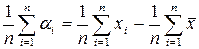 . (30)
. (30)
Откуда, с учетом (27), непосредственно следует первое равенство (29). Выражая из (28) xi и yi и подставляя их в выражение (26), получим после несложных, но несколько громоздких преобразований, рабочие формулы:
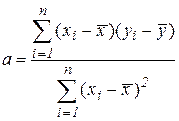 , (31)
, (31)
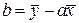 . (32)
. (32)
Вывод формул для погрешностей представляет значительно более сложную задачу, поэтому здесь мы его приводить не будем (интересующиеся этим вопросом могут посмотреть прил. 5 в кн. Сквайрс Дж. Практическая физика. – М.: Мир, 1971. – С. 46 – 50, 228 – 234). Для подсчета погрешностей 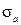 и
и 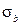 необходимо найти сумму квадратов отклонений экспериментальных точек от полученной наилучшей прямой
необходимо найти сумму квадратов отклонений экспериментальных точек от полученной наилучшей прямой
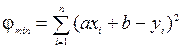 , (33)
, (33)
где a и b определены по формулам (31) и (32) или, если ввести обозначение
yi рас = a xi + b, (34)
то
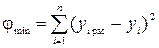 . (35)
. (35)
Тогда
 , (36)
, (36)
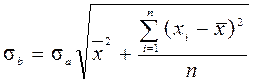 . (37)
. (37)
Доверительные интервалы для коэффициентов a и b при заданной доверительной вероятности 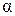 определяются по формулам:
определяются по формулам:
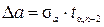 , (36’)
, (36’)
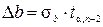 , (37’)
, (37’)
где коэффициенты 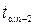 (или t (
(или t ( 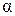 ; n – 2)) находят из таблиц для коэффициентов Стьюдента (см. табл. 2.)
; n – 2)) находят из таблиц для коэффициентов Стьюдента (см. табл. 2.)
| <== предыдущая страница | | | следующая страница ==> |
| Стандартная ошибка оценки | | |
Дата добавления: 2014-11-01; просмотров: 569; Нарушение авторских прав

Мы поможем в написании ваших работ!