
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Градусная и радианная мера угла
|
Читайте также: |
Геометрический угол-фигура, образованная двумя лучами, выходящими из одной точки – вершины угла.
1°(1 градус)= 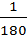 часть развернутого угла
часть развернутого угла
1рад (1 радиан)=центральный угол с длиной дуги равной радиусу окружности.
180°=π рад; n°= 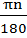 рад;K рад=
рад;K рад= 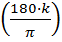 °
°
1°≈0,01745 рад; 1 рад≈57°17’45”
| Градусная мера | |||||||
| Радианная мера | 
| 
| 
| 
| π | 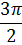
| 2π |
Тригонометрические функции любого угла.
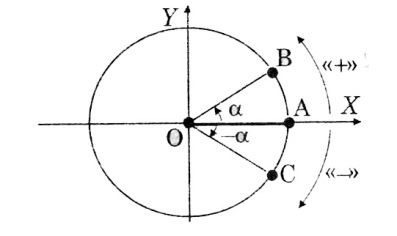
ОА – начальный радиус.α – угол поворота радиуса ОА при переходе в радиус ОВ.
Единичная окружность – окружность радиуса 1 с центром в т.О Если R = 1, то sin α = y, cos α = x
стр.1
Единичная окружность, значения синуса и косинуса.
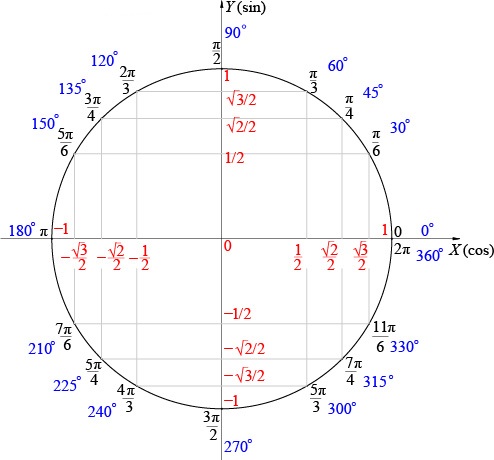
синус угла х-это отношение противолежащего катета к гипотенузе.
косинус угла х-это отношение прилежащего катета к гипотенузе.
стр.2
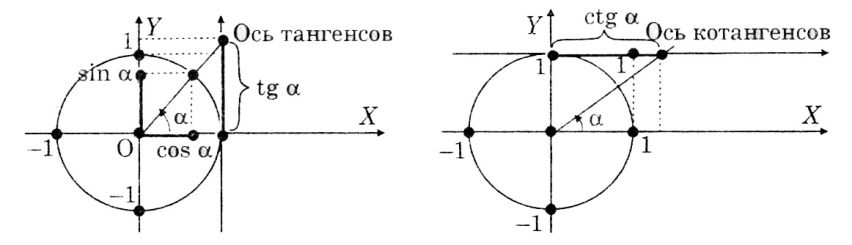
Единичная окружность значения тангенса и котангенса.
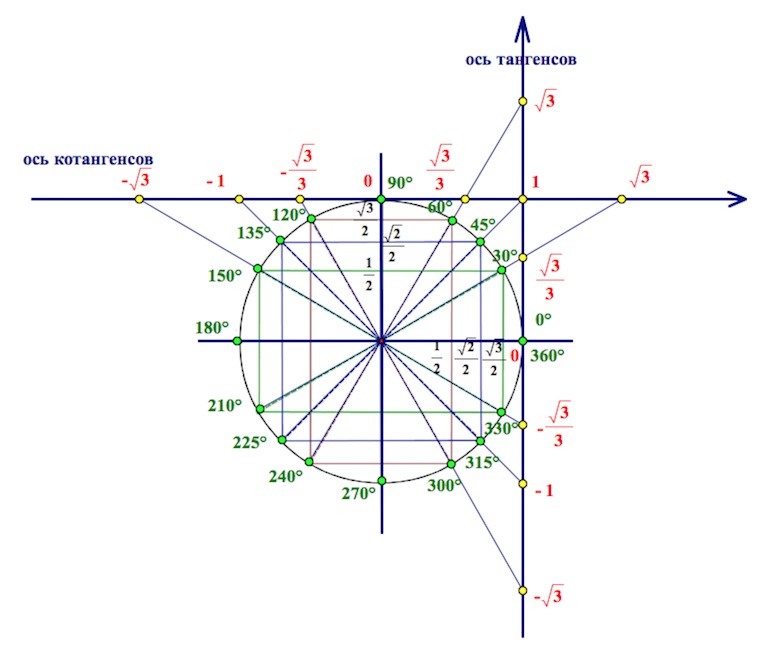
тангенс угла х-Это отношение противолежащего катета к прилежащему.
котангенс угла х-Это отношение прилежащего катета к противолежащему.
cтр.3
Графики f(x)=sin x, f(x)=cos x и их свойства.
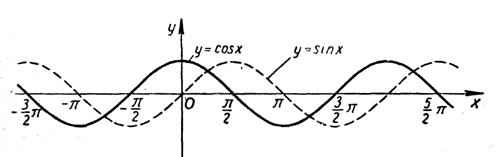
| у = sin x | у = cos x | |
| D(f): | R | R |
| E(f): | [-1;1] | [-1;1] |
| Нули функции | πn , n ∈ Z |  +πn , n ∈ Z +πn , n ∈ Z
|
| Промежутки Возрастания | [ -  +2πn; +2πn; 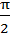 +2πn],
n ∈ Z +2πn],
n ∈ Z
| [ - π + 2πn; 2πn] , n ∈ Z |
| Промежутки Убывания | [  +2πn; +2πn; 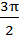 +2πn],
n ∈ Z +2πn],
n ∈ Z
| [2πn; π + 2πn] , n ∈ Z |
| Точки max |  +2πn , n ∈ Z +2πn , n ∈ Z
| 2πn, n ∈ Z |
| Точки min | 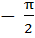 +2πn , n ∈ Z +2πn , n ∈ Z
| π + 2πn, n ∈ Z |
| y<0 | (- π + 2πn; 2πn) , n ∈ Z | ( -  +2πn; +2πn; 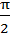 +2πn),
n ∈ Z +2πn),
n ∈ Z
|
| y>0 | (2πn; π + 2πn ), n ∈ Z | (  +2πn; +2πn; 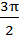 +2πn),
n ∈ Z +2πn),
n ∈ Z
|
cтр.4
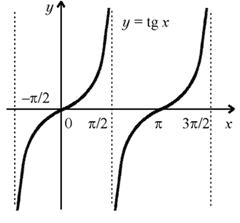
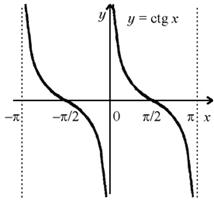
Графики f(x) = tg x, f(x) = ctg х и их свойства.
| у = tg x | у = ctg x | |
| D(f): | R | R |
| E(f): | ( 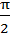 +2πn; +2πn; 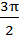 +2πn),
n ∈ Z +2πn),
n ∈ Z
| (2πn; π + 2πn ), n ∈ Z |
| Нули функции | πn , n ∈ Z | 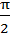 +πn , n ∈ Z +πn , n ∈ Z
|
| Промежутки Возрастания | ( - 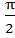 + πn; + πn;  +πn),
n ∈ Z +πn),
n ∈ Z
| |
| Промежутки Убывания | (πn; π + πn ), n ∈ Z | |
| Точки max | ||
| Точки min | ||
| y<0 | ( -  +πn; +πn;  +πn),
n ∈ Z +πn),
n ∈ Z
| ( -  +πn; +πn;  +πn),
n ∈ Z +πn),
n ∈ Z
|
| y>0 | (πn; π + πn ), n ∈ Z | (πn; π + πn ), n ∈ Z |
cтр.5
Тригонометрические формулы.
1. Тригонометрические функции числового аргумента:
sin2x + cos2x = 1-основное тригонометрическое тождество
tg x = 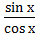 ; ctg x =
; ctg x = 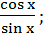 tg x · ctg x = 1;
tg x · ctg x = 1;
1 + tg2x = 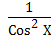 ; 1 + ctg2x =
; 1 + ctg2x = 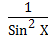 ;
;
2. Преобразование тригонометрических выражений:
sin (x ± y) = sin x · cos y ± cos x · sin y;
cos (x ± y) = cos x · cos y ± sin x · sin y.
3. Преобразование сумм тригонометрических функций в произведение:
sin a + sin b = 2 sin 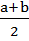 · cos
· cos 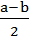 ;
;
sin a - sin b = 2 sin 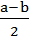 · cos
· cos 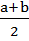 ;
;
cos a + cos b = 2 cos 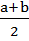 · cos
· cos 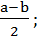
cos a - cos b = -2 sin 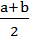 · sin
· sin 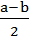 ;
;
tg(a 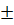 b)=
b)= 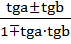 ;
;
cтр.6
4. Преобразование произведения тригонометрических
функций в суммы:
sin a · cos b =  (sin (a + b) + sin (a - b));
(sin (a + b) + sin (a - b));
cos a · cos b =  (cos (a + b) + cos (a – b));
(cos (a + b) + cos (a – b));
sin a · cos b =  (cos (a – b) – cos (a + b)).
(cos (a – b) – cos (a + b)).
5. Формулы кратных углов:
sin 2 x = 2 sin x· cos x; sin 3x = 3sinx- 4 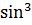 x;
x;
cos 2 x = cos2 x – sin2 x= 1-2sin2x = 2cos2x-1;
tg 2 x = 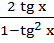 ; tg3x=
; tg3x= 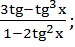
6. Формулы понижения степени:
cos2 a = 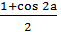 ; sin2 a =
; sin2 a = 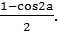
7. Преобразование выражения A sin x + B cos x:
A sin x + B cos x = C sin (x + t), где C = 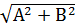 ,
,
t = arccos 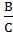 .
.
8. Решение простейших тригонометрических уравнений:
cos x = a; x = ± arccos a + 2 π n, n ∈ 2 при |a| ≤ 1;
sin x = a; x = (-1)n arcsin a + π n, n ∈ Z при |a| ≤ 1;
tg x = a; x = arctg a + π n, , n ∈ Z;
ctg x = a; x = arcctg a + π n, , n ∈ Z.
стр.7
Формулы приведения
1) Если под знаком преобразуемой тригонометрической формулы содержится сумма аргументов вида (π+t);(π+t);
(π-t);(2π-t);(2π-t); то наименование тригонометрической функции сохраняется.
2) Если под знаком преобразуемой тригонометрической формулы содержится сумма аргументов вида (  +t);(
+t);(  +t); (
+t); ( 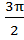 -t);(
-t);( 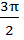 -t); то наименование тригонометрической функции стоит изменить (на родственное).
-t); то наименование тригонометрической функции стоит изменить (на родственное).
3) Перед полученной функцией от аргумента t нужно поставить тот знак, который имела бы преобразуемая функция при условии что: 0<t< 
Знаки тригонометрических функций:
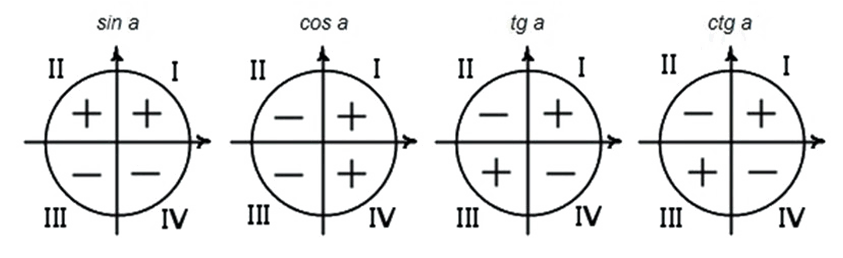
стр.8
| <== предыдущая страница | | | следующая страница ==> |
| Тестовые задания. 1. Модель дисконтирования дивидендов основана на следующем понятии | | | Рынок и рыночная экономика. Модели рыночной экономики |
Дата добавления: 2014-11-04; просмотров: 1230; Нарушение авторских прав

Мы поможем в написании ваших работ!