СИЛЫ В МЕХАНИКЕ

• Закон всемирного тяготения

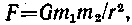
где F — сила взаимного притяжения двух материальных точек; m₁ и m₂ — их массы; r — расстояние между точками; G — гравита­ционная постоянная.

В написанной форме закон всемирного тяготения можно приме­нять и к взаимодействию шаров, масса которых распределена сфери­чески-симметрично. В этом случае r есть расстояние между центра­ми масс шаров.

• Напряженность гравитационного поля

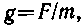
где F — сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.

• Напряженность гравитационного поля, создаваемого плане­той, массу М которой можно считать распределенной сферически-симметрично,

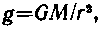
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

• Ускорение свободного падения на высоте h над поверхно­стью Земли

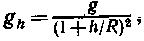
где R — радиус Земли; g — ускорение свободного падения на по­верхности Земли. Если 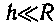, то

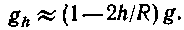
• Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m₁ и m₂ (шаров с массой, распре­деленной сферически симметрично), находящихся на расстоянии r друг от друга,

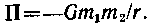
(Потенциальная энергия бесконечно удаленных друг от друга ма­териальных точек принята равной нулю.)

• Потенциал гравитационного поля

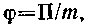
где П — потенциальная энергия материальной точки массой m, помещенной в данную точку поля.

• Потенциал гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-сим­метрично,

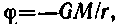
где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

• Законы Кеплера.

1. Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.

2. Радиус-вектор планеты в равные времена описывает одинако­вые площади.

3. Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит:

Законы Кеплера справедливы также для движения спутников вокруг планеты.

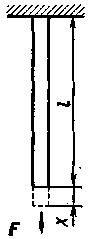
• Относительная деформация при продольном растяжении или сжатии тела

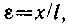
где ε — относительное удлинение (сжатие); x — абсолютное удли­нение (рис. 4.1); l — начальная длина тела.

Относительная деформация при сдвиге определяется из формулы

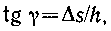
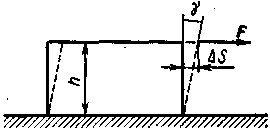
Рис. 4.1 Рис. 4.2

где — относительный сдвиг; Δs — абсолютный сдвиг параллель­ных слоев тела относительно друг друга (рис. 4.2); h — расстояние между- слоями; — угол сдвига. (Для малых углов )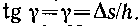

• Напряжение нормальное

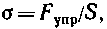
где Fynp — упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.

Напряжение тангенциальное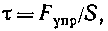

где Fynp — упругая сила, действующая вдоль слоя тела; S — площадь этого слоя.

• Закон Гука для продольного растяжения или сжатия

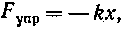или ,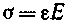

где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.

Закон Гука для сдвига

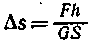, или ,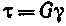

где G — модуль поперечной упругости (модуль сдвига).

• Момент, закручивающий на угол φ однородный круглый стер­жень,

,

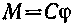где С — постоянная кручения.

• Работа, совершаемая при деформации тела,

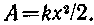
• Потенциальная энергия растянутого или сжатого стержня

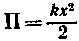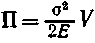, или , или ,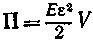
где V — объем тела.

Дата добавления: 2014-11-06; просмотров: 315; Нарушение авторских прав

Мы поможем в написании ваших работ!