
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТЕЛА, ДВИЖУЩИХСЯ ПОСТУПАТЕЛЬНО
• Уравнение движения материальной точки (второй закон Ньютона):
в векторной форме
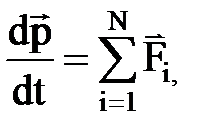 или
или 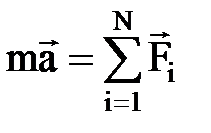
где 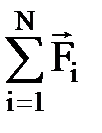 — геометрическая сумма сил, действующих на материальную точку; т — масса; а — ускорение; p=mv — импульс; N — число сил, действующих на точку;
— геометрическая сумма сил, действующих на материальную точку; т — масса; а — ускорение; p=mv — импульс; N — число сил, действующих на точку;
в координатной форме (скалярной)

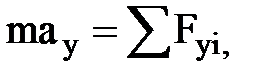
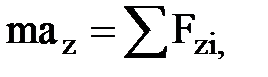 или
или 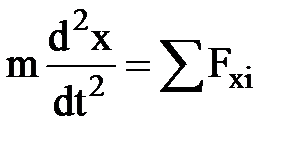 ,
, 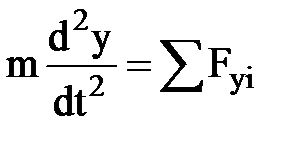 ,
, 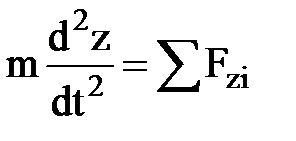
где под знаком суммы стоят проекции сил Fi, на соответствующие оси координат.
• Сила упругости *
Fупр=-
где k — коэффициент упругости (жесткость в случае пружины);
х — абсолютная деформация.
 Сила гравитационного взаимодействия *
Сила гравитационного взаимодействия *
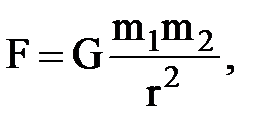
где G — гравитационная постоянная; m1 и m2 — массы взаимодействующих тел, рассматриваемые как материальные точки; r — расстояние между ними.
 Сила трения скольжения
Сила трения скольжения
Fтр=fN,
где f — коэффициент трения скольжения; N — сила нормального давления.
• Координаты центра масс системы материальных точек
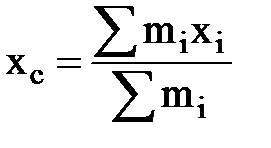 ,
, 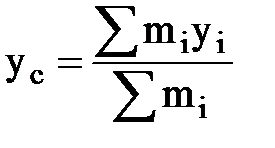 ,
, 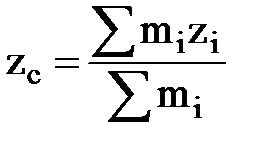
где mi — масса i-й материальной точки; xi, yi;, zi; — ее координаты.
• Закон сохранения импульса
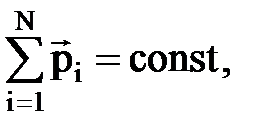 или
или 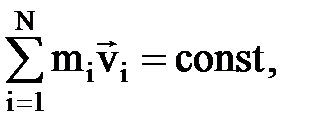
где N — число материальных точек (или тел), входящих в систему.
• Работа, совершаемая постоянной силой,
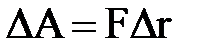 , или
, или 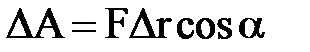 ,
,
где 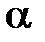 — угол между направлениями векторов силы F и перемещения
— угол между направлениями векторов силы F и перемещения  r.
r.
• Работа, совершаемая переменной силой,
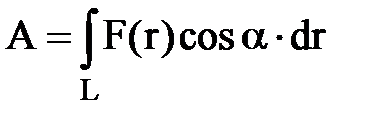
где интегрирование ведется вдоль траектории, обозначаемой L.
• Средняя мощность за интервал времени  t
t
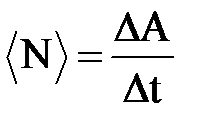 .
.
• Мгновенная мощность
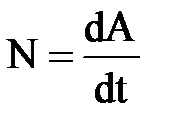 , или N=Fvcos
, или N=Fvcos 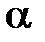 ,
,
где dA — работа, совершаемая за промежуток времени dt.
• Кинетическая энергия материальной точки (или тела), движущейся поступательно,
T=mv2/2, или T=p2/(2m).
• Потенциальная энергия тела и сила, действующая на тело в данной точке поля, связаны соотношением
F= - grad П или 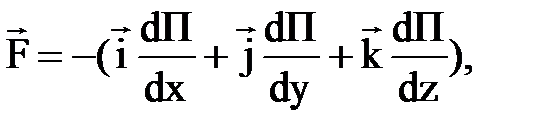 ,
,
где i, j, k — единичные векторы (орты). В частном случае, когда
* См. сноску на с. 19.
поле сил обладает сферической симметрией (как, например, гравитационное),
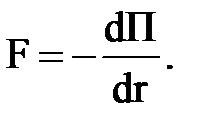
• Потенциальная энергия упругодеформированного тела (сжатой или растянутой пружины)
П=kx2/2.
Потенциальная энергия гравитационного взаимодействия двух материальных точек (или тел) массами m1, и т2, находящихся на расстоянии r друг от друга,
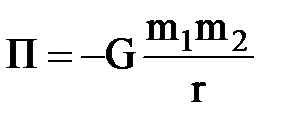
• Потенциальная энергия тела, находящегося в однородном поле силы тяжести,
П=mgh,
где h — высота тела над уровнем, принятым за нулевой для отсчета потенциальной энергии. Эта формула справедлива при условии h <<R, где R — радиус Земли.
• Закон сохранения энергии в механике выполняется в замкнутой системе, в которой действуют только консервативные силы, и записывается в виде
T+П== const.
• Применяя законы сохранения энергии и импульса к прямому центральному удару шаров, получаем формулу скорости абсолютно неупругих шаров после удара
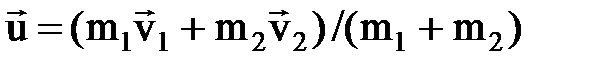 и формулы скорости абсолютно упругих шаров после удара:
и формулы скорости абсолютно упругих шаров после удара:
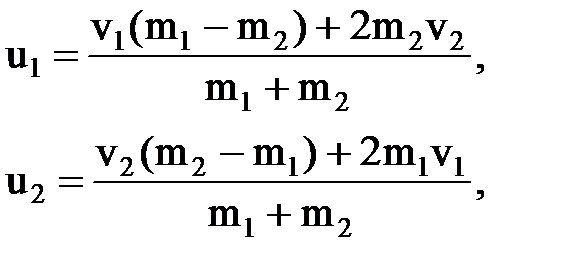
где m1 и m2 — массы шаров; v1 и v2 — их скорости до удара.
§ 3. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
• Момент силы F, действующей на тело, относительно оси вращения
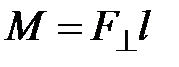 ,
,
где 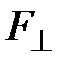 — проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
— проекция силы F на плоскость, перпендикулярную оси вращения; l — плечо силы F (кратчайшее расстояние от оси вращения до линии действия силы).
• Момент инерции относительно оси вращения:
а) материальной точки
J=mr2,
где т — масса точки; r — расстояние ее от оси вращения;
б) дискретного твердого тела
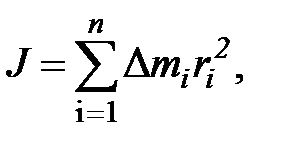
где 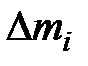 — масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;
— масса i-го элемента тела; ri — расстояние этого элемента от оси вращения; п — число элементов тела;
в) сплошного твердого тела
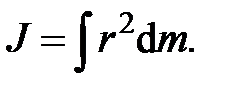
Если тело однородно, т. е. его плотность 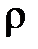 одинакова по всему объему, то
одинакова по всему объему, то
dm= 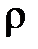 dV и
dV и 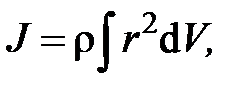
где V — объем тела.
• Моменты инерции некоторых тел правильной геометрической формы:
| Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
| Однородный тонкий стержень массой т и длиной l Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусом R и массой т, распределенной по ободу Круглый однородный диск (цилиндр) радиусом R и массой т Однородный шар массой т и радиусом R | Проходит через центр тяжести стержня перпендикулярно стержню Проходит через конец стержня перпендикулярно стержню Проходит через центр перпендикулярно плоскости основания Проходит через центр диска перпендикулярно плоскости основания Проходит через центр шара | 1/12ml2 1/3ml2 mR2 1/2mR2 2/5mR2 |
• Теорема Штейнера. Момент инерции тела относительно произвольной оси
J=J0+ma2,
где J0 — момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а — расстояние между осями; m — масса тела.
• Момент импульса вращающегося тела относительно оси
L=J 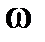 .
.
• Закон сохранения момента импульса
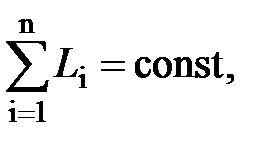
где Li — момент импульса i-го тела, входящего в состав системы. Закон сохранения момента импульса для двух взаимодействующих тел
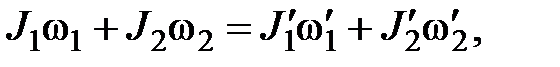
где 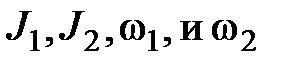 — моменты инерции и угловые скорости тел до взаимодействия:
— моменты инерции и угловые скорости тел до взаимодействия: 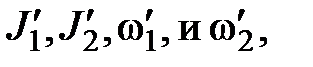 — те же величины после взаимодействия.
— те же величины после взаимодействия.
Закон сохранения момента импульса для одного тела, момент инерции которого меняется,
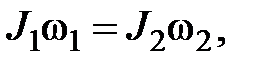
где 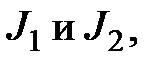 — начальный и конечный моменты инерции;
— начальный и конечный моменты инерции; 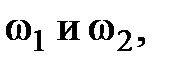 —• начальная и конечная угловые скорости тела.
—• начальная и конечная угловые скорости тела.
• Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
Mdt=d(J 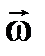 ), где М — момент силы, действующей на тело в течение времени dt;
), где М — момент силы, действующей на тело в течение времени dt;
J — момент инерции тела; 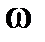 — угловая скорость; J
— угловая скорость; J 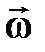 — момент импульса.
— момент импульса.
Если момент силы и момент инерции постоянны, то это уравнение записывается в виде
М  t=J
t=J  .
.
В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид
M=J 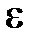 , где
, где 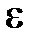 — угловое ускорение.
— угловое ускорение.
• Работа постоянного момента силы М, действующего на вращающееся тело,
A=Mj,
где j — угол поворота тела.
• Мгновенная мощность, развиваемая при вращении тела,
N=M 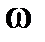 .
.
• Кинетическая энергия вращающегося тела
T=1/2J 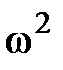 .
.
• Кинетическая энергия тела, катящегося по плоскости без скольжения,
T==1/2mv2+l/2J 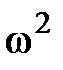 ,
,
где l/2mv2 — кинетическая энергия поступательного движения тела; v — скорость центра инерции тела; l/2J 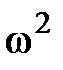 ,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
,— кинетическая энергия вращательного движения тела вокруг оси, проходящей через центр инерции.
• Работа, совершаемая при вращении тела, и изменение кинетической энергии его связаны соотношением
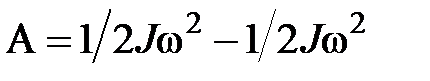 .
.
• Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения.
Эта аналогия раскрывается следующей таблицей:
Поступательное движение Вращательное движение
Основной закон динамики
F  t=mv2—mv1; M
t=mv2—mv1; M  t=J
t=J 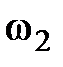 —J
—J 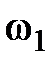 ;
;
F = та М = .J 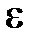
Закон сохранения
импульса момента импульса
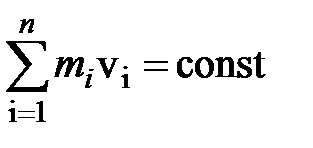
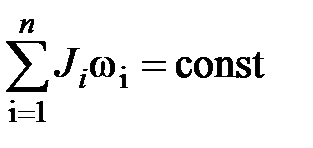
Работа и мощность
A=Fs; А=М 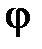 ,
,
N=Fv N=M 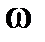
Кинетическая энергия
Т =1/2 mv2 T=1/2J 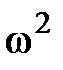
| <== предыдущая страница | | | следующая страница ==> |
| ГЛАВА 1 ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ | | | СИЛЫ В МЕХАНИКЕ |
Дата добавления: 2014-11-06; просмотров: 577; Нарушение авторских прав

Мы поможем в написании ваших работ!