Движения самой точки

Поэтому реакция 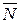заранее неизвестна.

Пример.

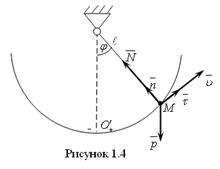
Рассмотрим движение груза M, подвешенного к нижнему концу гибкой нерастяжимой нити длиною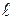

Уравнения (13) в данном случае имеют вид

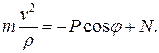
Откуда получаем

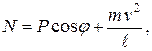
то есть реакция зависит от силы тяжести P, а также от положения точки на траектории, характеризуемого углом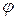, и её скорости 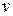в рассматриваемый момент времени.

3. Основные задачи динамики материальной точки.

В статике и кинематике мы решали две основные задачи. В динамике тоже мы будем решать две задачи.

Сначала будем рассматривать задачи для свободной материальной точке, а затем запишем замечания для несвободной материальной точки.

3.1 Первая основная (прямая) задача для свободной материальной точки. (стр 21 - 24)

Первая основная (прямая) задача.

Считая заданными массу и движение свободной материальной точки, требуется определить силу, которая вызывает заданное движение.

Рассмотрим решение этой задачи на конкретном примере.

Векторный способ задания движения точки(дополнительно)

Пусть дано:

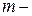масса точки;

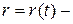уравнение движения точки в векторной форме.

Определить.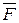

По заданному уравнению движения дифференцированием по времени находим вектор ускорения точки:

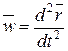
и, подставляя его в уравнение (1.6),определяем искомую силу

.

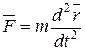Координатный способ задания движения точки(обязательно)

Пусть дано:

m – масса точки;

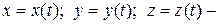уравнения движения точки.

Определить: модуль и направление силы.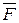

Дифференцируя дважды по времени уравнения движения, находим проекции ускорения точки на координатные оси

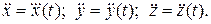
Затем воспользуемся уравнениями (1.8), из которых определяем проекции искомой силы

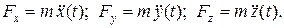
Эти проекции вполне определяют силу как величину векторную. Действительно, модуль силы равен

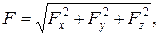
а её направление характеризуется выражениями

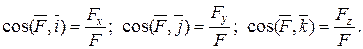
3адача

Материальная точка массой m движется согласно уравнениям

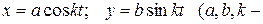постоянные).

Определить силу, вызывающую заданное движение точки. (модуль и направление)

Решение.

Воспользуемся следующими уравнениями:

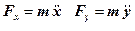
Определим вид траектории.

В кинематике мы рассматривали подобную задачу? Да.

Траекторией точки является эллипс

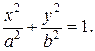
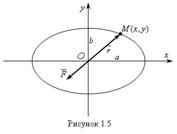
Находим проекции ускореий на координатные оси.

,

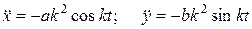т.к

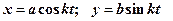
то данные уравнеия можно записать в другом виде

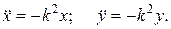
Отличие уравнений состоит в том, что в превом случае мы видим в чему равны производные в любой момент времени, а во втором случае в любом положении точки.

Следовательно проекции силы на оси координат будут равны:

,

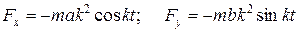или

Откуда

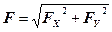
таким образом

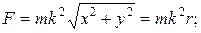
где

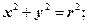
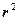- модуль радиуса вектора.

Сила действующая на точку , 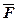– переменная, пропорциональная первой степени растояния до точки О начала координат.

Определим как она направленна.

Силу 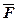предстовляем в виде:

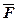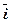= F_X + F_У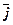

Подставляем

в данную формулу и получаем

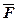= - mk²(x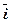+ у)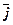

так как

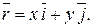
Итак

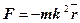
Чем отличается вектор силы от радиуса вектора?

Знаком и скаляром.

Сила 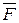в любом положении точки на эллипсе направлена в противоположную сторону вектора 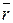, то есть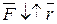

Таким образом, действующая на точку сила пропорциональна расстоянию точки от центра O , и её линия действия в любой момент движения проходит через неподвижный центр O.

Такая сила называется центральной силой. (она линейная ,т.к. пропорциональна первй степени радиуса вектора)

Первая задача динамики сточки зрения математики простая, т.к. решается с помощью операции дифференцирования.

Естественный способ задания движения точки (дополнительно)

Пусть дано:

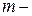масса точки;

траектория точки (следовательно, и её радиус кривизны );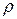

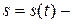уравнение движения точки в естественной форме (закон движения по траектории).

Определить: модуль и направление силы .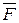

По уравнению движения точки вычисляем скорость, касательное и нормальное ускорения точки:

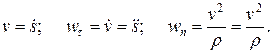
Далее из уравнения (1.10) находим проекции силы на естественные оси координат

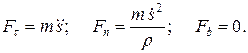
Наконец,

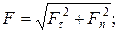
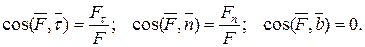
Итак, первая основная задача динамики свободной точки решается весьма просто при помощи операции дифференцирования.

Несмотря на свою простоту, эта задача сыграла важную роль в науке.

Опираясь на три эмпирических закона Кеплера (1571 ― 1630) ― немецкий математик и астроном, кинематически определяющих движение планет вокруг Солнца, Ньютон исследовал вопрос о том, какие силы действуют на планеты.

В результате решения этой первой задачи динамики Ньютон пришёл к открытию закона всемирного тяготения.

Первая задача динамики несовободной точки:

В случае несвободной точки в первой задаче динамики необходимо по заданной массе, активной силе, определить реакцию связей

3.2 Вторая основная (обратная) задача для свободной материальной точки. (стр. 24 – 28)

Формулировка.

Вторая основная (обратная) задача.

Считая известными массу точки, активную силу и начальное состояние точки, определить движение этой точки.

Под начальным состоянием точки понимают ее начальное положение и скорость в этом положении.

Следует иметь в виду, что под действующей на точку силой понимают равнодействующую только тех сил, которые действуют с начального момента времени. Силы же, действовавшие до начального момента времени, учитываются посредством задания начального положения точки и её начальной скорости.

Покажем, как решается эта задача, если способ задания движения координатный.

В общем случае проекции силы 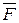зависят от функций времени, координат и проекций скорости точки

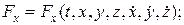
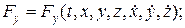(14)

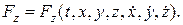
Запишем дифференциальные уравнения движения точки в координатной форме, Будем считать, что они нам заданы.

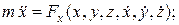
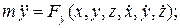(15)

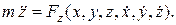
Итак, задача определения движения точки, т.е. нахождение x,у, z от t, сводится к интегрированию трех дифференциальных уравнений второго порядка

Общее решение этих уравнений будет содержать шесть произвольных постоянных.

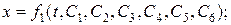
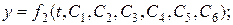(16)

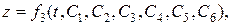
Итак мы получили шесть уравнений, которые имеют шесть неопределенных постоянных. Если задана сила она определяет не одно движение

Как видим ДУ движения точки при заданной силе 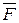, определяет не одно движение , а целый класс движений.

Возникает вопрос, почему так получается, ДУ известно, силы действующие известны и тем не менее определяем бесчисленное множество решений.

Рассмотрим пример, а потом я вам поясню как это получается, с точки зрения физики.

Пусть материальная точка – это мел.

Если это мел падает вниз под действием силы тяжести – это одно движение, Если при падении мела вниз с определенной высоты сообщить ему скорость, то он будет падать по параболе.

Можно бросить мел вверх сообщив ему ускорение, тогда он движется под углом к горизонту.

 

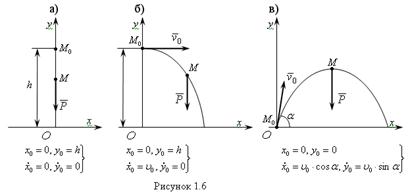Во всех трех задачах сила действует одна и та же, а движения тем не менее происходят разные.

Выходит движения зависят не только от действующей силы, но и от того ,где точка была в начале движения и какая у него при этом была скорость, т.е. от начального состояния.

Почему? Как это объяснить?

Сила определяет только ускорение, а скорость и положение точки на траектории определяют не только действующие силы, но и начальные положения и начальная скорость.

Таким образом, для того, чтобы задача была вполне определенной необходимо присоединить к этим уравнениям начальные условия

Чтобы получить вполне определенный закон движения точки к ДУ необходимо присоединить начальные условия.

Сколько этих условий будет?

Шесть, определяющие положение точки в начальный момент времени и скорость.

при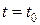

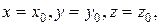(17)

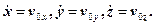
Здесь 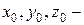начальные координаты;

проекции начальной скорости точки.

Что же мы должны делать при решении конкретной задачи. Уравнения (15) проинтегрировать , т.е. построить какое-то частное решение, которое бы удовлетворяло бы этим уравнениям и подставить начальные условия.

С точки зрения математики такая задача называется задачей Коши.

Следовательно данная задача механики сводиться к известной задачи Каши из теории ДУ ( О.Коши (1780-1857) – выдающийся французский математик.)

Для того, чтобы сформулировать вторую задачу динамики что необходимо знать?

Массу, силу, а необходимо найти закон движения и неизвестную реакцию.

Сформулируем вторую задачу динамики для несвободной точки.

В случае несвободной материальной точки, во второй основной задаче динамики, требуется по заданным массе, активной силе, начальному положению и начальной скорости точки определить движение точки и реакцию связей .

Какая задача более сложная для свободной, или не свободной?

Эта задача для несвободной материальной точки принципиально отличается от подобной задачи для свободной материальной точки.

При решении второй основной задачи динамики для свободной точки главное правильно составить дифференциальные уравнения движения, после чего их всегда можно проинтегрировать точно или приближёнными способами, известными из теории дифференциальных уравнений.

Для несвободной точки, мы не можем приступить непосредственно к интегрированию ДУ.

Дело в том, что в эти уравнения входят шесть неизвестных: три координаты x, y, z точки и три проекции N_x, N_y, N_z силы реакции 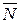, которая зависит не только от вида связи и активной силы 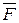, но и от самого движения точки. Поэтому прежде всего нужно каким бы то ни было способом исключить эту реакцию и только после этого можно приступить к интегрированию дифференциальных уравнений, уже не содержащих неизвестную реакцию, а затем по найденным уравнениям движения

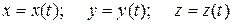
можно легко найти N_x, N_y, N_z

РС

При решении задач все силы можно разделить на силы зависящие от положения, скорости и времени.

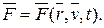
Примерами сил, зависящих от положения точки, являются упругая сила пружины, силы всемирного тяготения, кулоновы силы взаимодействия между зарядами.

К силам, зависящим от скорости, относятся силы сопротивления различных сред.

Сила, вызывающая колебания неуравновешенного мотора на упругом основании, служит примером силы, являющейся периодической функцией времени. К этому же классу сил относятся гидродинамические силы, действующие на винт корабля.

 

Дата добавления: 2014-03-24; просмотров: 580; Нарушение авторских прав

Мы поможем в написании ваших работ!