
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основные задачи динамики материальной точки
Естественная форма
3.1 Вторая основная (обратная) задача для свободной
материальной точки.
3.2 Первая основная (прямая) задача для свободной
материальной точки.
ЛИТЕРАТУРА:
1. Яблонский А.А. Курс теоретической механики. – М.: Высшая школа , 1971, ч 1 –2.
2. Тарг С.М. Краткий курс теоретической механики. – М: Высшая школа 1986.
3. Прусов В.М. Наголюк Л.О. Динамика – С.: СНУЯЭ и П, 2007.
4. Прусов В.М. Практические занятия по динамике С.:СВВМИУ 1985
5. Яблонский А.А Сборник заданий для курсовых работ по теоретической механике. М.: Высшая школа , 1985,
СТ. ПРЕПОДАВАТЕЛЬ
/КОРНЕЕВА Н.К./
ЛЕКЦИЯ № 15
ТЕМА: Законы динамики. Дифференциальные уравнения движения материальной точки.
Напоминаю, что объектом изучения статики являлось абсолютно твердое тело, находящееся в состоянии равновесия.
В кинематике мы изучали движение материальных объектов с геометрической точки зрения без учета масс и действующих на них сил.
Но не рассматривали, почему, то или иное тело так движется.
А теперь мы приступаем к изучению динамики, будем рассматривать движение, но уже с учетом действующих сил.
Динамика последний раздел курса теоретической механики. В этом разделе
Решаются самые общие задачи движения материального объекта.
Как и в кинематике, динамику подразделяют на два больших раздела:
- динамику материальной точки;
- динамику системы материальных точек и материального тела.
Начнем мы с изучения движения материальной точки, а затем уже перейдем к системе МТ.
Формулировка.
Динамика ― раздел теоретической механики, в котором движение изучается в зависимости от действующих сил и начального состояния.
В динамике будут решаться уравнения второго порядка и основные действия, которые необходимо будет выполнять - интегрирование
1. Основные законы динамики.
В основе динамики лежат известные вам законы Ньютона и изложенные им на латинском языке в трактате"Математические начала натуральной философии" (1687).
Сочинение Ньютона переведено на русский язык академиком А.Н.Крыловым (Известия морской академии, 1915; перепечатано в Собрании трудов акад. А.Н.Крылова, т. VII изд. АН СССР, 1936)
Портрет висит на стене.
Данные законы вам уже известны и из курса физики школьного, и институтского.
Законы Ньютона справедливы для тела, которое представляет собой свободную материальную точку.
Первый закон (закон инерции).
Формулировка
Изолированная от внешних воздействий материальная точка сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенная сила не заставит её изменить это состояние.
Свойство изолированной (от внешнего воздействия) материальной точки сохранять скорость - называется инертностью или инерцией.
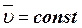
Согласно данному закону при движении материальной точки по инерции приложение силы не требуется.
Сама точка не может изменить свою скорость; скорость изменится только при действии на неё силы.
Другими словами, приобрести то или иное ускорение точка может только от внешнего воздействия.
В этой формулировке отсутствует очень важный момент, не указанна система отсчета.
Возникает вопрос.
Существует ли такая система отсчета, в которой справедлив закон динамики?
Как механики на этот вопрос отвечают?
Дают такое определение:
Систему отсчета, в которой выполняются закон инерции, - называется инерциальной или галлилеевой, а затем постулируют (воспринимают) существование такой системы и считают ее условно неподвижной.
Т. к. вам придется заниматься задачами динамики, которые происходят вблизи поверхности земли или на земле, в этом случае в качестве инерциальной системы берут так называемую земную (геоцентрическую)систему.
Угловая скорость вращения земли очень маленькая, поэтому можно ею пренебречь.
Это означает, что движением земли пренебрегают (движением вокруг оси и движением вокруг Солнца) и считают систему жестко связанную с землей системой инерциальной.
Это не значит, что такая система всегда может быть рассмотрена как инерциальная.
При решении задач космонавтики и астрономии:
В качестве инерциальной системы отсчета принимают гелеоценрическую (солнечную) систему отсчета, в которой данный закон выполняется с весьма высокой точностью.
В центре масс солнца помещают начало координат, а оси направляют к трем звездам, которые практически не меняют свое положение.
В северном полушарии левые берега размыты сильнее. Почему?
Это объясняется вращением земли. Скорость вращения земли маленькая, но реки текут веками. Возникает ускорение Кориолиса, которое приводит к тому, что правые берега размываются сильнее.
У железной дороги в северном полушарии все правые рельсы стерты сильнее, чем левые. Объясняется тоже вращением земли.
Но в большинстве случаев эту систему можно считать инерциальной.
Таких систем существует бесчисленное множество. Все системы, которые движутся поступательно и равномерно по отношению к первой системе тоже будут инерциальными.
Второй закон (основной закон динамики).
Во втором законе пойдет речь о зависимости между действующей силой приложенной к точке и ускорением.
В инерциальной системе отсчёта наиболее просто выполняется зависимость между действующей на материальную точку силой и вызываемым ее ускорением:
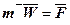 (1)
(1)
Формулировка
Произведение массы материальной точки на её ускорение, равно приложенной к ней силе.
Уравнение (1) называется основным уравнением динамики свободной точки.
Т.о. сила ¾ «причина», ускорение (вызываемое силой) ¾ «следствие».
Из уравнения (1) следует равенство:
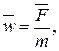 (2)
(2)
которое показывает, что при данной силе, чем больше ее масса 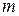 , тем меньше её ускорение.
, тем меньше её ускорение.
Это говорит о том, что точка:
- реагирует на действие силы, в результате получает ускорение,
- оказывает сопротивление при попытке изменить эту скорость. Данное свойство называется инертностью.
Какая величина является мерой инертности?
Масса. Чем больше масса, тем труднее изменить скорость этого объекта.
Запишем
Свойство материальной точки реагировать на внешнее воздействие, в результате которого она приобретает соответствующее ускорение, и оказывать при этом сопротивление изменению своей скорости, называется инертностью.
Количественной мерой инертности - является её масса.
Для того чтобы возникло ускорение необходимо внешнее воздействие.
Формула (1) устанавливает причинно-следственную связь.
| |
Формулировка
Силы, с которыми две материальные точки действуют друг на друга, всегда равны по модулю и направлены по одной прямой в противоположные стороны.
Данный закон относится не к одной материальной точке, а к системе из двух точек.
Всегда силы возникают попарно. Нет односторонне действующих сил.
Одну из сил взаимодействия двух материальных точек принято называть«действием», а другую ¾ «противодействием».
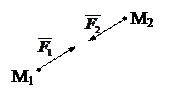 |
Данный закон кратко формулируют следующим образом:
всякое действие вызывает равное и противоположно направленное противодействие.
Чем так важен это закон? О чем он говорит?
О этот закон говорит о том, что для того, чтобы возникла сила необходимо наличие хотя бы двух тел.
Силы всегда возникают попарно. Нет односторонне действующих сил.
Силы, о которых говорится в этом законе, не уравновешивают друг друга и не могут быть отброшены, так как они приложены к разным материальным точкам.
Силы взаимодействия будут образовывать уравновешенную систему только в частном случае, когда обе материальные точки принадлежат одному и тому же абсолютно твёрдому телу.
Пример.
В руке мел. Земля на него воздействует – силой тяжестью. Мел действует на землю такой же по величине силой.
Но так как масса земли огромна по сравнению с массой этого тела, мы пренебрегаем действием этого мела на землю, и тогда у нас получается точка, и мы изображаем одну силу, хотя на самом деле строго необходимо изображать две силы.
Но если взаимодействие существенно, тогда рассматривается задача на движение не одной точки, а системы материальных точек.
Еще существенно, если мы собираемся изучать движение не одной точки одиночки, то закон поможет нам основные законы динамики для точки как-то ухитрится обобщить на случай системы материальных точек.
Подведем итоги.
Замечание 1
Первый и второй законы выполняются в инерциальной системе отсчета.
Третий закон справедлив в любой системе отсчёта.
Замечание 2
Первый, второй и третий законы справедливы только для свободной точки.
На первый взгляд кажется, что достаточно трех законов, чтобы описать движение точки в различных случаях.
Ничего подобного.
Во первых, когда мы записывали формулу (1), предполагалось , что на точку действует одна сила , а не несколько сил.
Во вторых, мы считали, что нет связей. Точка свободная. А на практике к точке прикладывается не одна сила, а несколько (система) и наложены ограничения – связи.
Для того чтобы в дальнейшем можно было бы решать любую задачу по динамике точке нам необходимо рассмотреть еще два закона.
Четвёртый закон (закон независимости действия сил).
Этот закон позволяет применять второй закон Ньютона к свободной материальной точке, на которую действует не одна сила, а несколько сил.
Пусть на материальную точку действует система сил 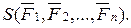
Формулировка
Если на материальную точку действует одновременно несколько сил, то ускорение точки равно сумме тех ускорений, которые получила бы точка под действием каждой силы в отдельности,
то есть
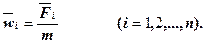 (4)
(4)
где 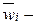 ускорение, вызываемое силой
ускорение, вызываемое силой 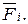 ,которая вызывает изменение скорости, т.е ускорение
,которая вызывает изменение скорости, т.е ускорение
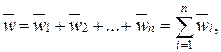 (5)
(5)
Каждая сила действует в системе независимо от других, другие силы не мешают данной силе вызвать свое ускорение, и т.д. для всех остальных.
Принято говорить, чтосилы действуют независимо, от того, действует ли одна только эта сила или все 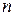 сил одновременно.
сил одновременно.
Подставляя выражение (5) в формулу (4), получаем
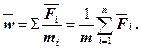
Откуда
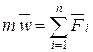
Введем обозначение 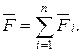
откуда
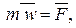
Формулировка
Из формулы (5) видно, что точка под действием системы сил 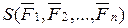 движется так, как если бы к материальной точке была бы приложена одна сила равная сумме всех действующих сил.
движется так, как если бы к материальной точке была бы приложена одна сила равная сумме всех действующих сил.
В статике эта сила называлась равнодействующей.
Это означает, что в динамике, как и в статике, систему сил 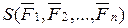 , действующих на материальную точку, можно заменить равнодействующей этой системы сил.
, действующих на материальную точку, можно заменить равнодействующей этой системы сил.
Всегда ли мы рассматриваем только свободную точку? Что мы делали в статике, когда тело было не свободным?
Освобождали от связей.
В динамике, как и в статике, применяется закон освобождаемости от связей.
Пятый закон (закон освобождаемости от связей).
Этот закон говорит о том, что для несвободной точки связи можно отбросить, заменив их на реакции и рассматривать тело, находящееся под действием активных сил и реакций связи
Формулировка
Всякую несвободную материальную точку, находящуюся в любом движении, можно освободить от связей, заменив действия связей их реакциями, и рассматривать её как свободную, находящуюся под действием приложенных активных сил и реакций связей.
Этот закон называют также принципом освобождаемости от связей.
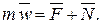 (6)
(6)
где
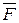 - равнодействующая всех активных сил,
- равнодействующая всех активных сил,
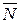 равнодействующая всех реакций связей,
равнодействующая всех реакций связей,
Формула (6) выражает основноеуравнение движения несвободнойматериальной точки
2.Дифференциальные уравнения движения материальной
точки.
Для того, чтобы описать движение материального объекта находящегося под действием сил, необходимо составлять дифференциальные уравнения, а потом их решать.
Решение дифференциальных уравнений называется интегрированием дифференциальных уравнений.
Как известно из кинематики, движение точки математически можно описать тремя способами:
· векторным,
· координатным
· естественным.
Соответственно, из второго закона Ньютона следуют дифференциальные уравнения движения материальной точки
· ввекторной,
· в координатной
· в естественной
формах.
2.1 Векторная форма
Рассмотрим свободную материальную точку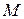 массы
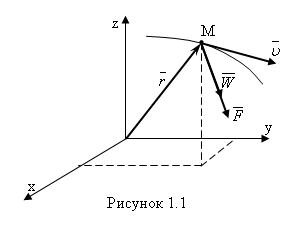
массы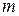 , движущуюся под действием системы сил
, движущуюся под действием системы сил 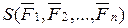 относительно инерциальной системы отсчёта (рисунок 1.1).
относительно инерциальной системы отсчёта (рисунок 1.1).
Исходным уравнением является основной закон динамики :
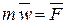 . (1)
. (1)
Изображаем координатную систему Оxyz – это инерциальная система отсчета, принято называть движение по отношению к инерциальной системе отсчета абсолютным движением.
Изобразим точку М и силу  .
.
Если посмотреть на первое уравнение, то чем отличается вектор силы от вектора ускорения в скалярной величине?
Скаляром массы.
Значит в этом случае сила и ускорение направлено по одной прямой.
 |
 |
Если воспользоваться формулой
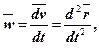
где  радиус – вектор точки, то уравнение (1) принимает вид
радиус – вектор точки, то уравнение (1) принимает вид
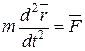 (7)
(7)
Уравнение (7) называется дифференциальным уравнениемдвижениясвободной материальной точки в векторной форме.
Для несвободной точки в правой части появится, кроме активной силы реакция.
Записываем.
Для несвободной точки уравнение (6) записывается:
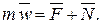
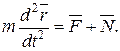 (8)
(8)
Где
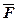 - равнодействующая всех активных сил
- равнодействующая всех активных сил
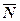 - равнодействующая всех реакций связи
- равнодействующая всех реакций связи
Уравнение (8) называется дифференциальным уравнением движениянесвободной материальной точки в векторной форме.
2.2 Координатная форма
Проецируя векторное равенство (7) на координатные оси, получаем скалярные уравнения
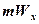 = Fx
= Fx
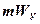 = Fу
= Fу
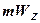 = Fz
= Fz
где
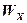 =
= 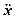
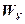 =
= 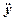
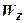 =
= 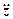
поэтому
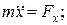
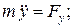 (9)
(9)
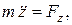
Уравнения (9) называютсядифференциальнымиуравнениями свободной материальнойточки в координатной форме (декартовых координатах).
Очевидно, дифференциальные уравнения движения несвободной точкив декартовых координатах имеют вид
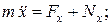
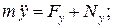 (10)
(10)
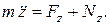
Уравнения (9) называютсядифференциальнымиуравнениями не свободной материальнойточки в координатной форме (декартовых координатах).
Существуют диф. уравнения первого, второго и др. порядков, зависят эти уравнения от старшей производной.
2.3 Естественная форма
Для записи диф. уравнений в естественной форме необходимо вспомнить кинематику.
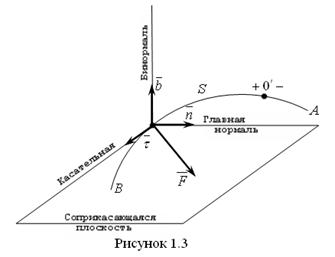
Если траектория АВ точки М известна, то изображаем:
- траекторию движения точки,
- начало отсчета
- точку на траектории.
Затем изображаем естественную систему координат, для этого проводим касательную Направление касательной определяем ортом 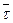 , затем изображаем главную нормаль и бинормаль, характеризуемые соответственно ортами
, затем изображаем главную нормаль и бинормаль, характеризуемые соответственно ортами 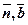
Плоскость образованную касательной и главной нормалью называют соприкасающейся плоскостью.
Теперь будем проецировать основное уравнение (1) на естественные оси.

Для свободной материальной точки
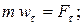
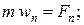 (11)
(11)
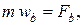
или
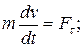
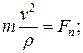 (12)
(12)
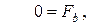
так как
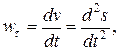
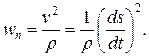
Из последнего уравнения (11) видно, что траектория, описываемая точкой под действием силы 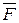 , такова, что соприкасающаяся плоскость всегда содержит в себе эту силу.
, такова, что соприкасающаяся плоскость всегда содержит в себе эту силу.
Уравнения (11) называются дифференциальными уравнениями движениясвободной материальной точки вестественной форме.
По аналогии легко записать дифференциальные уравнения движениянесвободной точки в естественной форме
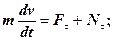
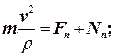 (13)
(13)
Замечание:
Реакция 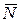 зависит от:
зависит от:
1) типа связей, наложенных на точку;
2) активной силы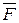 , вызывающей движение точки: реакция может появиться только при наличии активной силы;
, вызывающей движение точки: реакция может появиться только при наличии активной силы;
| <== предыдущая страница | | | следующая страница ==> |
| Определяют длину линии по формуле | | | Движения самой точки |
Дата добавления: 2014-03-24; просмотров: 999; Нарушение авторских прав

Мы поможем в написании ваших работ!