Механика. Идеальной жидкостью называется воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутренне трение и теплопроводность

Вопрос 9

Идеальной жидкостью называется воображаемая несжимаемая жидкость, в которой отсутствуют вязкость, внутренне трение и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости.

Модель идеальной жидкости используется при теоретическом рассмотрении физических задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. В частности, такая модель применима во многих задачах гидроаэромеханики, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Математическое описание течений идеальных жидкостей позволяет найти теоретическое решение ряда задач о движении жидкостей и газов в каналах различной формы, при истечении струй и при обтекании тел.

Для графического изображения течения жидкости часто используют линии тока - линии, касательная к которым в каждой точке совпадает с вектором скорости частицы. При этом линии тока рисуют так так, чтобы густота линий тока (число линий, пронизывающих площадку единичной площади в перпендикулярном им направлении) была бы пропорциональна величине вектора скорости. В случае стационарного течения картина линий тока не изменяется, а сами они совпадают с траекториями движения молекул жидкости.

Поверхность, образованная линиями тока, проведенными через все точки замкнутого контура, называется трубкой тока.

При стационарном течении жидкости ее молекулы не пересекают трубку тока.

Рассмотрим течение идеальной жидкости внутри некоторой трубки тока, обладающей такими сечениями, что скорость молекул жидкости в любой точке каждого из них одинакова. Так как идеальная жидкость несжимаема, то ее масса, сосредоточенная между сечениями S1 и S2 трубки тока, с течением времени не изменяется. Поэтому объемы жидкости dQ, протекшие через эти сечения за промежуток времени dt, будут равны. Поскольку dQ = S•v•dt, то выполняется соотношение:

S•v = const (1)

Это выражение называется уравнением неразрывности. Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.

Уравнение Бернулли и следствия из него

Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость. Пусть в месте сечения S1 скорость течения v1, давление p1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление p2 и высота сечения h2. За малый промежуток времени t жидкость перемещается от сечения S1 к сечению , от S2 к .

Согласно закону сохранения энергии, изменение полной энергии E2—E1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы m жидкости:

E2 – E1 = А, (30.1)

где E1 и E2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени t. Для перенесения массы m от S1 до жидкость должна переместиться на расстояние l1=v1t и от S2 до — на расстояние l2=v2t. Отметим, что l1 и l2 настолько малы, что всем точкам объемов, закрашенных на рис. 47, приписывают постоянные значения скорости v, давления р и высоты h. Следовательно,

А = F1l1 + F2l2, (30.2)

где F1=p1S1 и F2= – p2S2 (отрицательна, так как направлена в сторону, противоположную течению жидкости)

Полные энергии E1 и E2 будут складываться из кинетической и потенциальной энергий массы m жидкости:

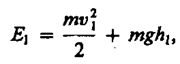(30.3)

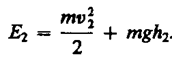(30.4)

Подставляя (30.3) и (30.4) в (30.1) и приравнивая (30.1) и (30.2), получим

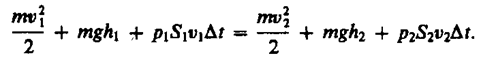
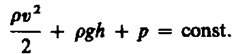
(30.6)

Выражение (30.6) выведено швейцарским физиком Д. Бернулли (1700—1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико.

Величина р в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина v2/2 — динамическим давлением. Как уже указывалось выше (см. § 28), величина gh представляет собой гидростатическое давление.

Для горизонтальной трубки тока (h1 =h2) выражение (30.6) принимает вид

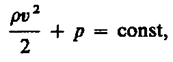(30.7)

где p+v2/2 называется полным давлением.

Вязкость (внутреннее трение) — это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

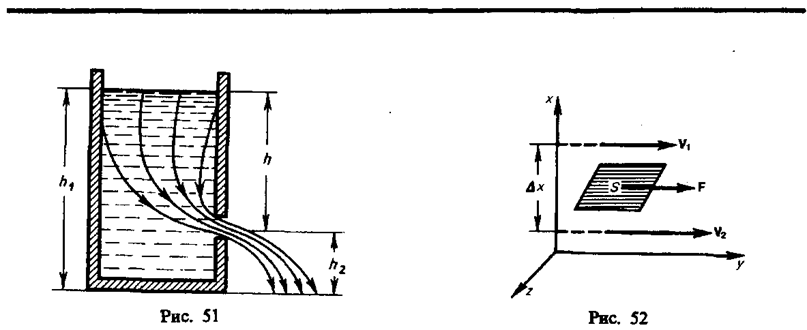
Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S (рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. На рисунке представлены два слоя, отстоящие друг от друга на расстоянии x и движущиеся со скоростями v1 и v2. При этом v1—v2=v. Направление, в котором отсчитывается расстояние между слоями, перпендикулярно скорости течения слоев. Величина 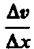показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направлению движения слоев, и называется градиентом скорости. Таким образом, модуль силы внутреннего трения

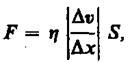
где коэффициент пропорциональности , зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью).

Единица вязкости — паскаль-секунда (Па-с): 1 Па-с равен динамической вязкости среды, в которой при ламинарном течении и градиенте скорости с модулем, равным 1 м/с на 1 м, возникает сила внутреннего трения 1 Н на 1 м2 поверхности касания слоев (1 Па-с= 1 Н-с/м2).

Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей и газов различен (для жидкостей  с увеличением температуры уменьшается, у газов, наоборот, увеличивается), что указывает на различие в них механизмов внутреннего трения. Особенно сильно от температуры зависит вязкость масел. Например, вязкость касторового масла в интервале 18—40°С падает в четыре раза. Российский физик П. Л. Капица (1894—1984; Нобелевская премия 1978 г.) открыл, что при температуре 2,17 К жидкий гелий переходит в сверхтекучее состояние, в котором его вязкость равна нулю.

Существует два режима течения жидкостей. Течение называется ламинарным (слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа).

Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Скорости последующих слоев тем больше, чем больше их расстояние до поверхности трубы, и наибольшей скоростью обладает слой, движущийся вдоль оси трубы.

При турбулентном течении частицы жидкости приобретают составляющие скоростей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы, затем изменяется довольно незначительно. Так как частицы жидкости переходят из одного слоя в другой, то их скорости в различных слоях мало отличаются. Из-за большого градиента скоростей у поверхности трубы обычно происходит образование вихрей.

Вопрос 11

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

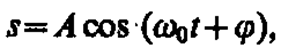
где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, 0 — круговая (циклическая) частота,  — начальная фаза колебания в момент времени t=0, (0t+) — фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2п, т. е.

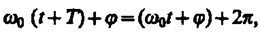
Откуда

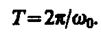(140.2)

Величина, обратная периоду колебаний,

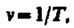(140.3)

т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим

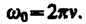Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

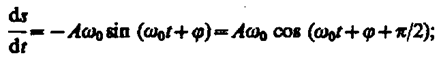(140.4)

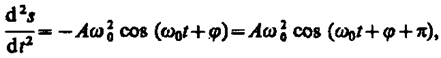(140.5)

т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны А0 и А . Фаза величины (140.4) отличается от фазы величины (140.1) на /2, а фаза величины (140.5) отличается от фазы величины (140.1) на . Следовательно, в моменты времени, когда s=0, ds/dt приобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d2s/dt2 приобретает наибольшее положительное значение (рис. 198).

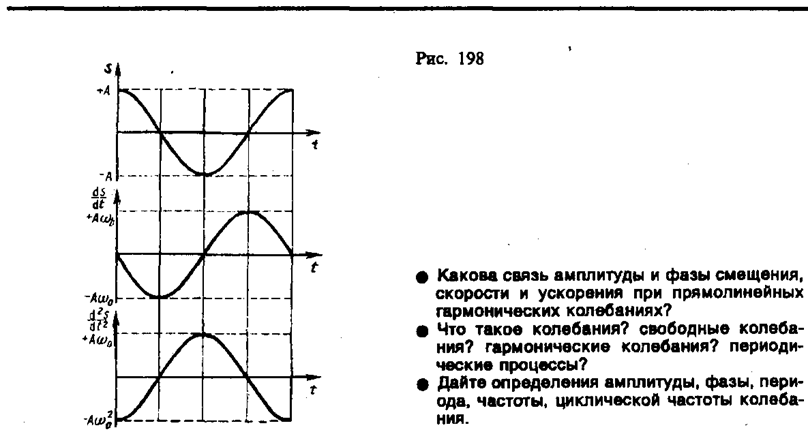
Из выражения (140.5) следует дифференциальное уравнение гармонических колебаний

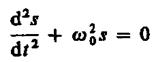(140.6)

(где s = A cos (0t+)). Решением этого уравнения является выражение (140.1).

Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины. Уравнение движения маятника

(142.1)

Из выражений (142.1) и (140.1) следует, что пружинный маятник совершает гармонические колебания по закону х=А соs (0t + ) с циклической частотой

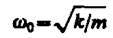(142.2)

и периодом

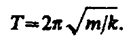(142.3)

Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением

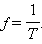
Чaстота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов процесса, совершённых за единицу времени. Стандартные обозначения в формулах — , , или . Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом.

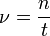
Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины. Амплитуда — модуль максимального отклонения тела от положения равновесия.

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние , в котором он находился в первоначальный момент, выбранный произвольно).

Обозначения: обычное стандартное обозначение периода колебаний: Т

Единицы измерения: секунда

Период колебаний связан соотношением взаимной образности с частотой:

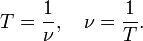
Фа́за колеба́ний — аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс.

Фаза колебания это дробная часть t/T периода T, на которую t сдвинуто относительно произвольного начала координат. Началом координат обычно считается момент предыдущего перехода функции через нуль в направлении от отрицательных значений к положительным.

В большинстве случаев о фазе говорят применительно к гармоническим (синусоидальным или описывающимся мнимой экспонентой) колебаниям (или монохроматическим волнам, также синусоидальным или описывающимся мнимой экспонентой).

Для таких колебаний:

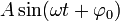
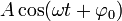
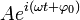
Вопрос 12

затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Закон затухания колебаний определяется свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, в которых параметры, определяющие физические свойства системы, в ходе процесса не изменяются. Линейными системами являются, например, пружинный маятник при малых растяжениях пружины (когда справедлив закон Гука), колебательный контур, индуктивность, емкость и сопротивление которого не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются идентичными линейными дифференциальными уравнениями, что позволяет подходить к изучению колебаний различной физической природы с единой точки зрения, а также проводить их моделирование, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

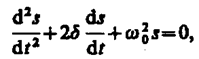(146.1)

где s – колеблющаяся величина, описывающая тот или иной физический процесс, =const — коэффициент затухания, 0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы

Решение уравнения (146.1) рассмотрим в виде

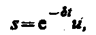(146.2)

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

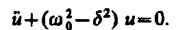(146.3)

Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:

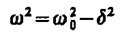(146.4)

(если ( )>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа , решением которого является функция и=А0cos(t+) Таким образом, решение уравнения в случае малых затуханий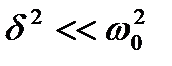

коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. По существу, коэффициент затухания определяется логарифмическим декрементом и характеризует диссипацию акустической энергии, вызванную внутренним трением. В связи с этим для оценки диссипирующей способности материала используют тангенс угла механических потерь, определенный при звуковых частотах. Он связан с физико-механическими, физико-химическими свойствами, составом, структурой и текстурой полимерного материала.

ДЕКРЕМЕНТ ЗАТУХАНИЯ количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону. T. к. в линейной системе колеблющаяся величина изменяется по закону 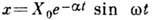(где постоянная величина 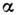- коэф. затухания) и два последующих наиб. отклонения в одну сторону X1 и X2 (условно наз. "амплитудами" колебаний) разделены промежутком времени 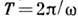(условно наз. "периодом" колебаний), то 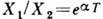, а Д. з.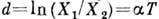

Так, напр., для механич. колебат. системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф. упругости k и испытывающей трение силой FT, пропорциональной скорости v (FТ =-bv, где b - коэф. пропорциональности), Д. з.

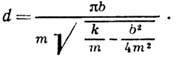
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и t+T

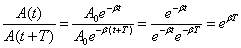
где β – коэффициент затухания.

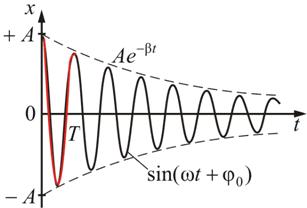
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:

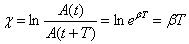
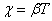
Выясним физический смысл χ и β.

Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.

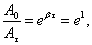отсюда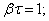

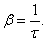
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда

; ;

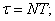
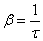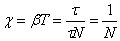
логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

Дата добавления: 2014-11-06; просмотров: 458; Нарушение авторских прав

Мы поможем в написании ваших работ!