Л4 Механика электропривода

1 Одномассовая модель электропривода.

Для анализа поведения ЭП как механической системой необходимо все статические моменты и силы нагрузки, а также все моменты и массы инерции, действующие в реальной системе ЭП, приводить к базовой угловой скорости. В качестве последней принимают угловую скорость вала ЭД

С этой целью реальные ЭП с достаточной степенью точности могут быть представлены в виде жесткой одномассовой механической системы со статическим моментом нагрузки Мс и приведенным моментом инерции Y, угловая скорость которой соответствует угловой скорости вала электродвигателя

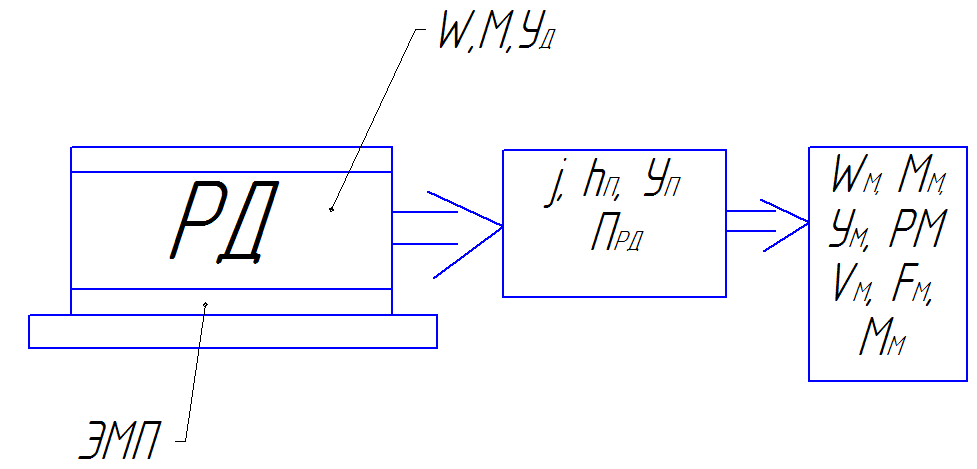
Механическая часть электродвигателя

ЭМП – электромашинный преобразователь

РД – ротор двигателя

Прд - передаточное устройство

РМ – рабочая машина (механизм)

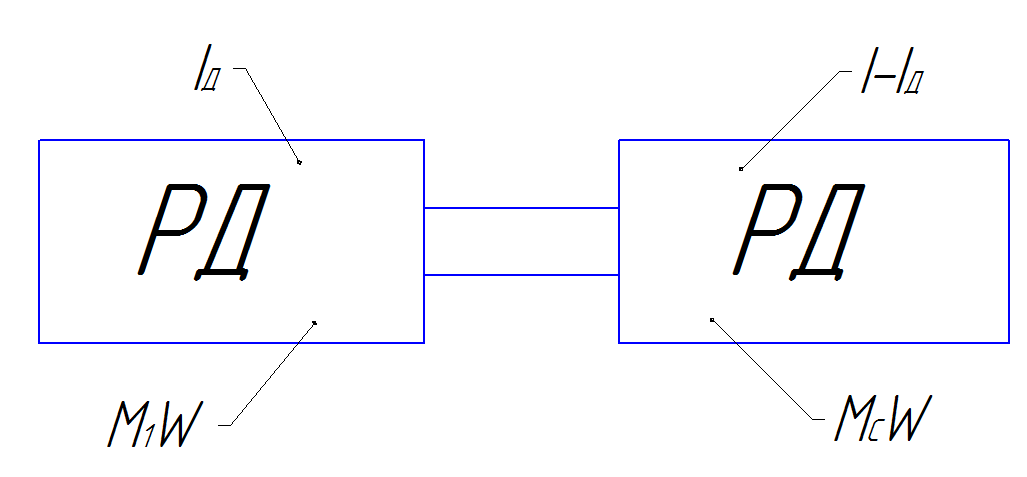
Приведение моментов и сил статического сопротивления.

Его выполняют на основании рассмотрения энергетического баланса для механической части ЭП, который сводят к равенству мощностей одномассовой и реальной систем в установившемся режиме, при котором вращающий момент двигателя М уравновешено моментом статической нагрузки M=Mc:

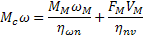
Общее правило - что бы привести статический момент к валу двигателя, нужно реальный статический момент на валу рабочего органа разделить на передаточное число и КПД передачи.

Окончательно получим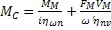

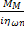– расчетное соотношение для приведения моментов нагрузки

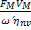– расчетное соотношение для приведения сил нагрузки.

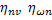- соответственно КПД механической передачи исполнительных органов, совершающих вращательное и поступательное движения,

Мм, Fм – момент (Нм) и сила, Н, статической нагрузки от исполнительных органов

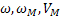- угловые скорости двигателя и исполнительных органов вращательного движения рад/с, и линейная поступательного, (м/с)

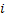– передаточное отношение механической передачи от двигателя к исполнительным органам вращательного движения, .

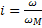Приведение фактических моментов и масс инерции к угловой скорости вала электродвигателя массовой модели электропривода.

Его осуществляют на основании равенства кинетической энергии искомого приведенного момента инерции Y, масса которого вращается с угловой скоростью вала электродвигателя.

Сумма кинетических энергий вращательно (Yд, 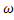и Yм, ω 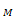) и поступательно ( движущихся частей ЭП запишутся: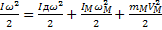

В результате приведения статического момента и момента инерции к валу двигателя получаем уравнение движения ЭП: M-Mc= 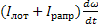или M-Mc=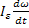

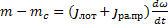или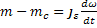

C учетом инерционности механической передачи получаем расчетную формулу по проведению моментов и масс инерции к валу электродвигателя

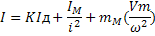
где K=1.05 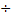1.2 коэффициент, учитывающий момент инерции механической передачи

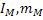– соотв. момент инерции (кгм² ) и масса (кг) вращательно и поступательно движущихся частей рабочей машины.

В справочных данных на электродвигатели исполнительные органы рабочих машин иногда вместо момента инерции I (кг/м² ) приводят значение махового момента GД² в Нм² или кг/м² .

В этом случае момент инерции

I = GД² /4g (а) или I = GД² /4 (б)

где

G – сила тяжести, Н – для (а) и кг для (б)

Д – диаметр инерции, (м)

g – ускорение свободного падения, g = 9.81 м/с²

Момент инерции простых тел можно рассчитать. Например, момент инерции цилиндра Мц с внешним Rц и внутренним rц радиусами относительно продольной осевой линии равны

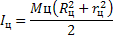
Для физических тел сложной конфигурации и совершающих сложные движения используют методы экспериментального определения моментов инерции. Например, используют экспериментальные методы крутильных и маятниковых колебаний, метод падающего груза, а так же метод свободного выбега.

Метод свободного выбега. Этот метод наиболее удобен для экспериментального нахождения момента инерции всей системы электропривода, особенно когда рабочие органы машины или механизма совершают сложные движения.

В этом случае предварительно определяют зависимость мощности, затрачиваемой на приведение в движение механической системы при разных угловых скоростях. Затем систему разворачивают до номинальной или близкой к ней угловой скорости и, отключив двигатель от сети, опытным путем определяют продолжительность 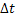прохождения системой фиксируемого малого перепада угловой скорости . Зная эти показатели, на основании уравнения движения одномассовой системы рассчитывают ее приведенный момент инерции , кгм² :

Где мощность х.х. затраченная на приведение в движение системы при скорости Вт:

-среднее значение угловой скорости в в диапазоне рад/с

Механические характеристики производственных механизмов и электродвигателей.

Механические характеристики производственных механизмов. Рабочая машина в виде производственного механизма создаёт на приводном валу момент статической нагрузки 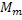, значение которого определённым образом связано с угловой скоростью приводного вала механизма 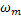. Зависимость 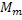= 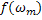называют механической характеристикой производственного механизма.

В общем случае множество механических характеристик различных производственных механизмов с достаточной степенью точности можно описать соотношением:

,

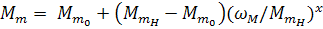Где 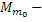начальный момент статической нагрузки от сил трения-движения,

равный ориентировочно моменту нагрузки на приводном валу при угловой скорости близкой к нулю, то есть из рассмотрения исключается момент от сил трения-покоя,

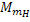– момент статической нагрузки при номинальной угловой скорости 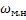; x – показатель степени, характеризующий изменение момента статической нагрузки 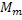при изменении угловой скорости приводного вала механизма .

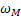Классификация. В зависимости от целочисленного значения “x” механические характеристики производственных механизмов подразделяют на четыре основные группы:

1. Не зависимая от скорости механическая характеристика х=0, (1). Все ГП мех. (лебёдки, краны, лифты, ленточные конвейеры, цепные, скребковые - от сил трения-движения.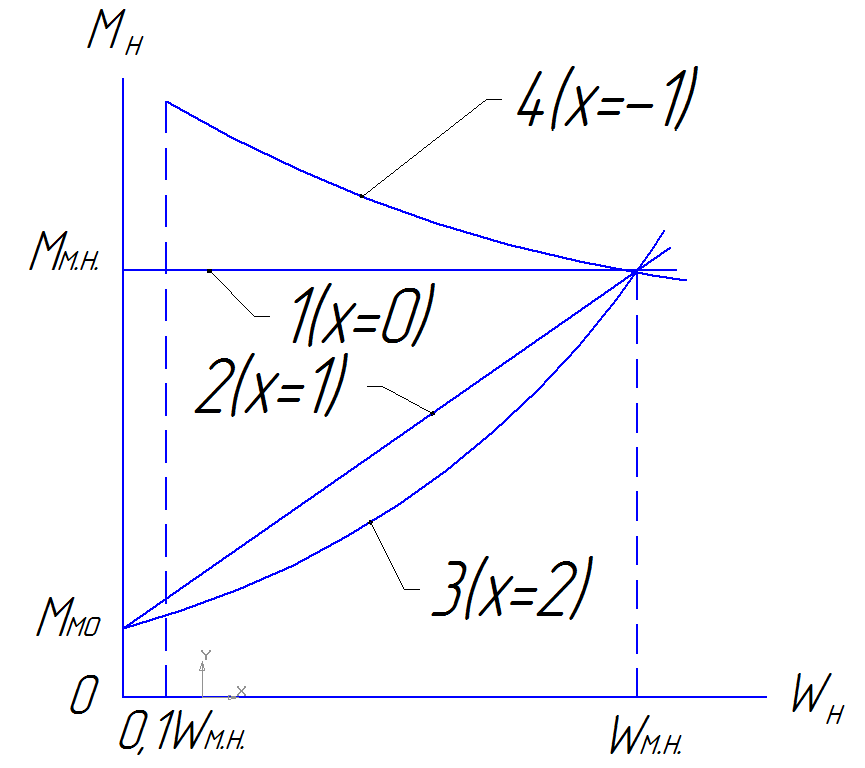

2. Линейно-возвращающая характеристика, х=1, (2) Такой характеристикой обладает установка с генератором постоянного тока независимо возбуждающийся постоянным сопротивлением нагрузки (измельчители сочных кормов режущего типа).

3. Нелинейно возрастающая (вентиляторная) механическая характеристика, х=2, (3) Такую характеристику имеют центробежные механизмы (вентиляторы, насосы, работающие без противодавления)

4. Нелинейно убывающая механическая характеристика для угловых скоростей, начиная от >0, 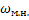х=-1, (4) Ограничение по скорости необходимо, так как при 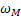=0 момент нагрузки равен бесконечности ( 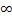), что нереально. Такая характеристика свойственна гл. приводу металлорежущих станков (токарных, фрезерных, сверлильных). Так как мощность на валу двигателя определяется соотношением P= 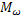, то она с изменением угловой скорости вала изменяется в степени “х+1”.

Статический момент, действующий со скоростью производственных механизмов, может быть реактивным (пассивным) и активным. Реактивный момент (характеристика 1 и 2) возникает при движении механизмов и всегда направлен противоположно направлению движения. Он всегда тормозной, так как обусловлен силами трения.

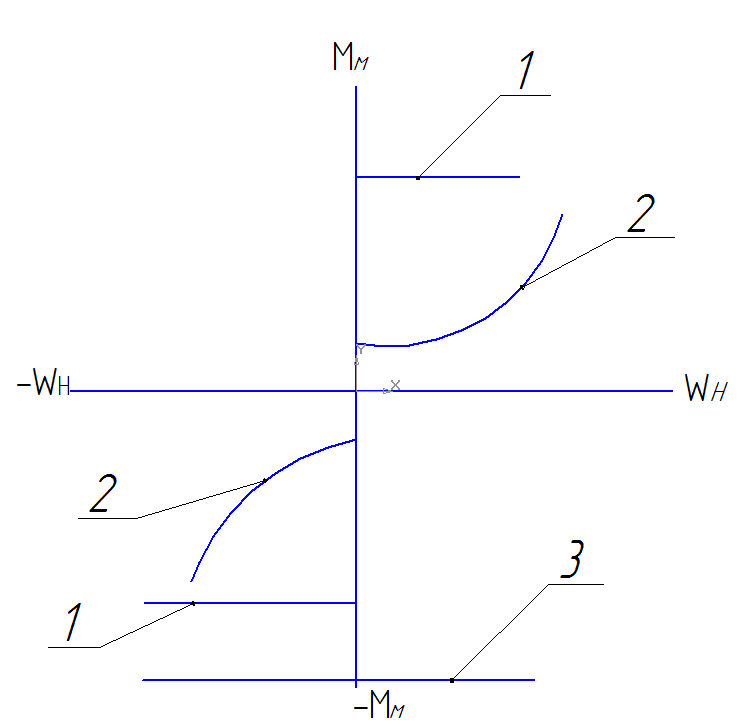
Активный момент (характеристика 3) создаётся независимо от наличия и направления движения и является однонаправленным. Он может быть и тормозным и движущим, так как обусловлен внешней однонаправленной силой, в качестве которой может выступать вес груза, сила упругого деформированного элемента, напор жидкости.

Уравнение движения электропривода.

Кинематическую энергию, Дж, движущихся в системе ЭП масс можно на основании одномассовой модели выразить в виде:

,

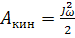Где 𝚥 – приведённый момент инерции ЭП, кг

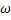- угловая скорость вала ЭД, рад/с

Если в результате внешних возмущений происходит изменение угловой скорости вала электродвигателя, то в системе ЭП возникает динамическая нагрузка, мощностью:

=

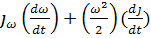
При этом значение возникающего динамического момента на основании соотношения M = составит:

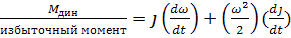(1)

Используя связь между угловым путём вала электродвигателя 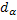, угловой скоростью 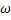и временем dt как dt = 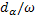и подставляя это во второе слагаемое, также учитывая что на основании одномассовой модели ЭП 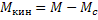, получим дифференциальное уравнение двигателя ЭП в одном виде.

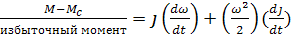(2)

В большинстве случаев 𝚥=const, то есть d𝚥/dα = 0 тогда уравнение сведётся ко второму закону Ньютона для вращательного движения с представлением углового ускорения через первую производную от угловой скорости 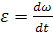, рад/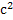

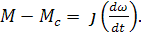(3)

Левая часть равенств 1 и 2 представляется собой избыточный момент 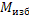, а правая – динамический момент 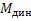, которые в системе ЭП равны м в любой момент времени друг друга уравновешивают. Для поступательного движения на основании (3) имеем

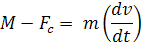
Где 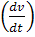=α – линейное ускорение механической системы, м/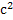

Переходные процессы электропривода.

Виды и особенности переходных процессов электропривода.

Переходным процессом или динамическим режимом ЭП называют режим перехода ЭП из одного установившегося состояния в другое, в процессе которого происходит изменение соответствующих видов энергии.

Переходные процессы имеют место при пуске, торможении, реверсировании угловой скорости ЭП, при изменении его нагрузки и условий электропитания. При этом происходит изменение соответствующих видов энергии: электромагнитной, механической и тепловой. Соответственно и названия происходимых процессов: электромагнитный, механический и тепловой. В ряде случаев при совместном рассмотрении электромагнитного и механического переходных процессов выделяют электромеханический.

Электромагнитные и механические переходные процессы в ЭП происходят значительно быстрее тепловых, поэтому их рассматривают по отдельности. Механические переходные процессы возникают в ЭП при пуске, реверсе и электрическом торможении ЭП. Принятие конкретного способа пуска, реверса или электрического торможения ЭП определяется, во-первых, видом используемого электродвигателя и, во-вторых, требованиями со стороны технологической установки, приводимой им в действие.

Из-за инерционности системы ЭП переходный процесс происходит в течение определённого интервала времени. Кривую 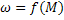. Момент в переходном процессе называют динамической механической характеристикой двигателя в системе конкретного ЭП, которая, как правило отличается от статической механической характеристики.

При пуске и реверсе асинхронных ЭП с полным напряжением питания максимального значения моментов. АД по динамической механической характеристике не могут превышать его номинальный момент:

При пуске 3-5 раз

При реверсе 12-18 раз.

Электромагнитная постоянная времени 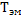существенно меньше механической постоянной времени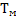

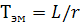
L – индуктивность АД, Г

r – активное сопротивление обмотки АД, Ом

Механическая постоянная времени асинхронного ЭП.

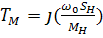
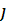– приведённый момент нагрузки системы (Д-РМ), кг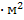

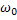- синхронная угловая скорость

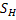- скольжение при номинальной нагрузке

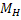- номинальный вращающий момент двигателя, н.м.

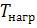- постоянная времени нагрева составляет 10 – 35 минут.

Наиболее благоприятное протекание электромеханического переходного процесса происходит в ЭП с управляемыми режимами пуска и торможения.

Интервал времени от поступления сигнала на пуск до начала вращения двигателя называют продолжительность запаздывания.

Эта продолжительность тем больше, чем значительнее нагрузка ЭП и чем медленнее изменения на якоре двигателя (МПТ) от сигнала управления. Причём чем выше темп нарастания напряжения, тем больше избыточный момент, действующий со стороны двигателя ЭП, тем меньше продолжительность его пуска.

Расчет продолжительности пуска и торможения электропривода.

Допуская постоянства момента инерции ЭП в соответствии с его основным уравнением движения (3), можно записать:

dt = 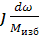, (4)

где 𝚥 - приведенный момент инерции ЭП, кг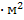

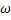- угловая скорость вала электродвигателя рад/с

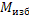– избыточный момент ЭП, нм.

Для определения продолжительности механического переходного процесса ЭП необходимо проинтегрировать (4) необходимых пределах изменения угловой скорости, т.к. 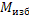представляет собой сложную функциональную зависимость 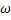, то прибегают к численному интегрированию (4):

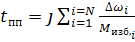, (5)

где 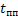- продолжительность переходного процесса, с.

N – число участков , на которые разбивается интервал ЭП

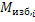- среднее значение избыточного момента на рассматриваемом i-м участке, нм.

В частности, продолжительность пуска или торможения ЭП 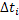на любом выделенном участке перепада угловых скоростей 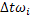, на котором действует средний избыточный момент 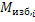, рассчитывают по обобщенной формуле:

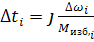(6)

Очевидно что для получения полной продолжительности того или иного переходного процесса полученные частные значения 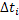следует просуммировать:

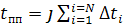(7)

На основании (5, 6, 7) в качестве примера приведем необходимые графические построения для определения 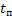асинхронного ЭП с вентиляторной нагрузкой на валу.

Порядок расчетов и построений:

1. Рассчитывают и строят механическую характеристику двигателя ЭП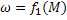

2.
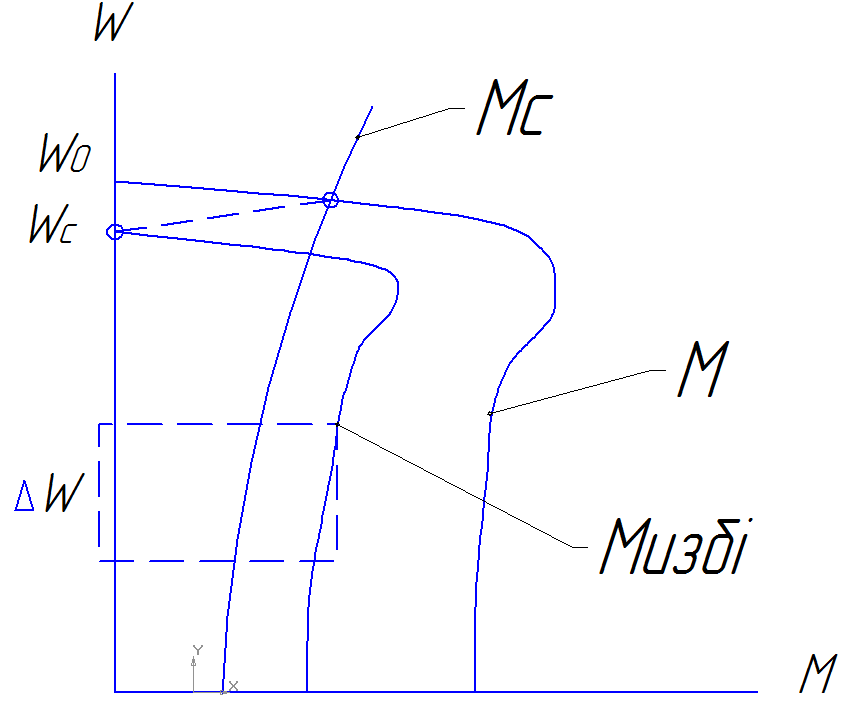
Рассчитывают и строят механическую характеристику рабочей машины, приведенную к валу ЭД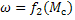

3. Для выбранных угловых скоростей 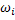рассчитывают значения избыточного момента 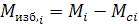и по ним строят кривую избыточного момента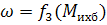

4. На выбранных интервалах значения угловой скорости определяют средние значения избыточных моментов 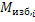и на основании (6, 7) расчитывают продолжительность переходного процесса.

Для оценочных расчетов при пуске ЭП с малой нагрузкой или торможением ЭП под действием постоянного момента нагрузки, допустимо использовать один участок скоростного интервала 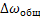и вести расчет по формуле

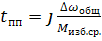
Иногда при выборе интенсивность механического переходного процесса ЭП оценивают коэфициентом интенсивности пуска (торможения)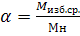

Где Мн –номинальный вращающий момент электродвигателя.

Дата добавления: 2014-05-03; просмотров: 1571; Нарушение авторских прав

Мы поможем в написании ваших работ!