
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ИССЛЕДОВАНИЕ СТАНКА-КАЧАЛКИ
Задачей исследования является проведение структурного и кинематического анализа станка-качалки. Структурное исследование механизма сводится к определению структуры механизма и его подвижности. Кинематическое исследование ставит целью определение скоростей точек механизма и угловых скоростей звеньев. Студентам предлагается решение данных задач для конкретно заданного положения механизма, на примере ниже приведенной методики.
Дано: радиус кривошипа станка-качалки rmax=AB=1500 мм (1,5 м), K=ED=2000 мм, K1=DC=2500мм, l=CB=1700 мм; l1=2500 мм, l2=2300 мм, число оборотов станка-качалки (число качаний балансира) - n =10 об/мин; положение механизма задано при угле поворота α=350º кривошипа АВ.
Исследование станка-качалки начинается с построения механизма в заданном положении при соответствующем угле поворота кривошипа - α.
1.1. Построение заданного положения механизма
Построение механизма производится в масштабе длины 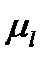 , определяемое отношением действительной длины звена к его изображению ни рисунке 4:
, определяемое отношением действительной длины звена к его изображению ни рисунке 4:
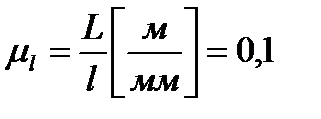 (1)
(1)
Тогда отрезок, соответствующий длине кривошипа АВ будет равен:
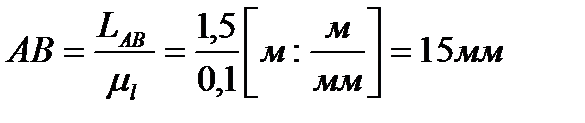
| E0 |
| C0 |
| A |
| B |
| D |
| l2 |
| l1 |
| E |
| C |
| B0 |
| α=350 º |
Рис.4 Построение начального и заданного положений механизма.
Построение заданного положения механизма следует начать с выбора произвольной точки А стойки кривошипа, от которой откладывается отрезок АВ0 в левую сторону по горизонтали, что соответствует нулевому положению механизма. Заданный угол положения кривошипа получим, отсчитывая от нулевого положения величиной α по направлению движения часовой стрелки радиусом rmax, что определит положение точки В.
| E |
| C |
| A |
| B |
| D |
| l2 |
| l1 |
Рис. 5 Механизм в заданном положении
Положение точки D опоры коромысла (балансира СК) определяем, откладывая расстояние l1 по горизонтали от опоры А влево и расстояние l2 на вверх масштабе 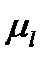 , что будет соответствовать (рисунок 5):
, что будет соответствовать (рисунок 5):
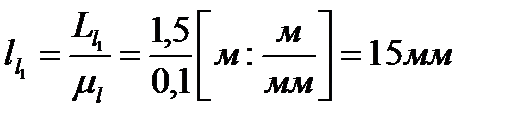
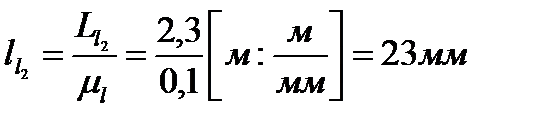
Из конца кривошипа - точки В, длиной отрезка l1 в масштабе 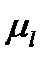 проводим след траектории движения точки С звена ВС (дугу радиуса ВС). Из точки D длиной К1 траекторию точки С звена DC (дуга радиуса DC). Пересечение дуг определит точки С′ и C″, из которых за расположение точки С выбирается ближайшее. Из точки С через точку D проводим отрезок СE, принимая отрезок DE, равным K, в масштабе
проводим след траектории движения точки С звена ВС (дугу радиуса ВС). Из точки D длиной К1 траекторию точки С звена DC (дуга радиуса DC). Пересечение дуг определит точки С′ и C″, из которых за расположение точки С выбирается ближайшее. Из точки С через точку D проводим отрезок СE, принимая отрезок DE, равным K, в масштабе 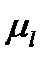 .
.
1.2. Структурный анализ станка-качалки
|
Рис.6 Структурная схема станка-качалки |
Шарнирный четырехзвенник включает в себя звенья:
0 – стойка – неподвижное звено;
1 – кривошип – звено, совершающее вращательное движение;
2 – шатун – совершает плоскопараллельное движение;
3 – коромысло – совершает неполное поворотно-вращательное движение.
Звенья связаны друг с другом кинематическими парами. Структурная формула имеет вид: В01→В12→ В23→В30.
Подвижность механизма определяется по формуле Чебышева:
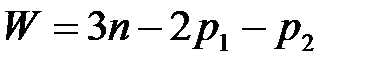 , (2)
, (2)
где 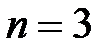 – число подвижных звеньев;
– число подвижных звеньев;
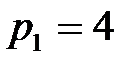 – число кинематических пар низших, одноподвижных 5-го класса;
– число кинематических пар низших, одноподвижных 5-го класса;
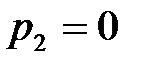 – число кинематических пар двухподвижных 4-го класса.
– число кинематических пар двухподвижных 4-го класса.
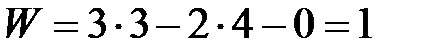 .
.
1.3. Кинематическое исследование станка-качалки
В данной контрольной работе кинематическое исследование станка-качалки основывается на графоаналитическом методе построения плана скоростей.
Для построения плана скоростей задаем полюс р в произвольной точке пространства. Точка полюса соответствует точке механизма с нулевой скоростью (рисунок 7).
Определим угловую скорость первого звена с заданным законом движения, выраженным частотой вращения n об/мин:
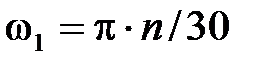 , (3)
, (3)
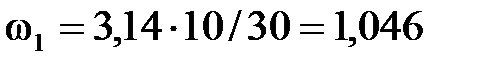 рад/с.
рад/с.
Скорость точки А равна нулю 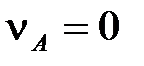 , так как точка А принадлежит стойке. Скорость точки В находим по формуле:
, так как точка А принадлежит стойке. Скорость точки В находим по формуле:
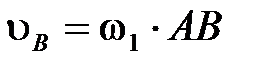 , (4)
, (4)
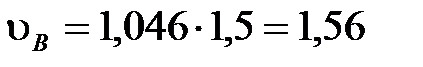 м/с.
м/с.
Проводим из полюса pv вектор 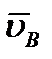 , который направлен перпендикулярно звену АВ в сторону его вращения. Для удобства построения плана скоростей (графического изображения скоростей на плоскости) зададим произвольно длину отрезка pв, изображающего скорость точки B. В данном случае для наглядности удобнее принять масштаб не 1:1, а увеличить план в 2 раза, поэтому примем
, который направлен перпендикулярно звену АВ в сторону его вращения. Для удобства построения плана скоростей (графического изображения скоростей на плоскости) зададим произвольно длину отрезка pв, изображающего скорость точки B. В данном случае для наглядности удобнее принять масштаб не 1:1, а увеличить план в 2 раза, поэтому примем 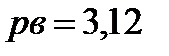 см.
см.
Рассчитаем масштаб плана скоростей:
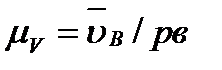 , (5)
, (5)
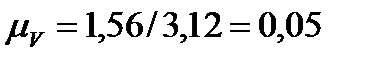
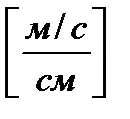
Для определение скорости точки С, принадлежащей двум звеньям 2 и 3, составим векторную систему уравнений, которая решается графически:
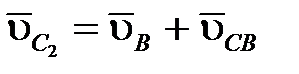 , (6) , (6)
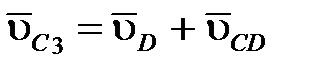 . .
|
Вектор 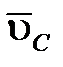 перпендикулярен звену ВС и из точки в проводим линию, перпендикулярную ВС. Пересечение отрезка рв с перпендикуляром отрезка CD получим в точке с,что определит длину отрезка рс.Вектор
перпендикулярен звену ВС и из точки в проводим линию, перпендикулярную ВС. Пересечение отрезка рв с перпендикуляром отрезка CD получим в точке с,что определит длину отрезка рс.Вектор 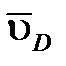 перпендикулярен звену СD – с полюса р проводим линию, перпендикулярную СD.
перпендикулярен звену СD – с полюса р проводим линию, перпендикулярную СD.
Скорость точки D равна нулю 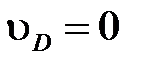 , следовательно, точка D находится в полюсе. Чтобы найти отрезок ре, решаем пропорцию на основе подобия плана скоростей и механизма, измеряя линейкой полученный отрезок рс:
, следовательно, точка D находится в полюсе. Чтобы найти отрезок ре, решаем пропорцию на основе подобия плана скоростей и механизма, измеряя линейкой полученный отрезок рс:
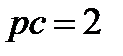 см
см
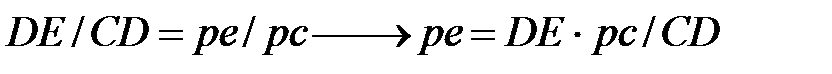 (7)
(7)
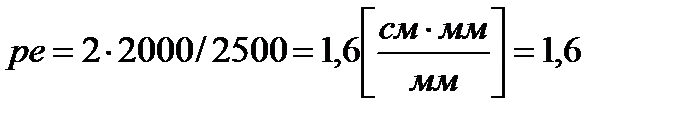 см.
см.
| b |
| p |
| c |
| e |
| ┴ AB |
| ┴ BC |
| ┴ CD |
| d |
Рис.7 План скоростей механизма
По плану скоростей находим скорости:
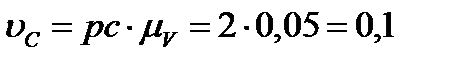 м/с2, (8)
м/с2, (8)
 м/с2,
м/с2,
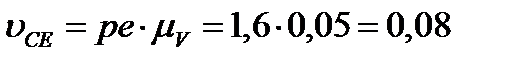 м/с2.
м/с2.
Далее находим угловые скорости и показываем их направления:
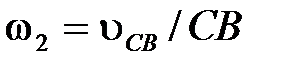 , (9)
, (9)
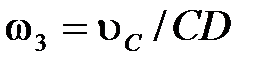
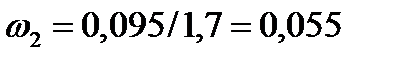 рад/с,
рад/с,
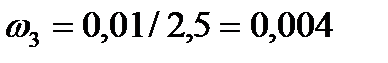 рад/с.
рад/с.
Направление угловых скоростей звеньев определяем по направлению векторов скорости 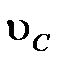 и
и 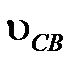 (рисунок 8).
(рисунок 8).
| E |
| 0 |
|
| 3 |
| 2 |
| 1 |
| C |
| A |
| B |
| D |
| ω3 |
| ω2 |
| ω1 |
Рис.8 Механизм с указанием направления вращений звеньев
| <== предыдущая страница | | | следующая страница ==> |
| ЗАДАНИЕ | | | ПРОЕКТИРОВАНИЕ И РАСЧЕТ ПРИВОДА СТАНКА-КАЧАЛКИ |
Дата добавления: 2014-11-06; просмотров: 485; Нарушение авторских прав

Мы поможем в написании ваших работ!