
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Внешние и внутренние силы.Напряжения. Метод сечений
Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые называются внешними. Внешние силы, действующие на тело, можно разделить на активные (независимые) и реактивные. Реактивные усилия возникают в связях, наложенных на тело, и определяются действующими на тело активными усилиями.
По способу приложения внешние силы делятся на объемные и поверхностные.
Объемные силы распределены по всему объему рассматриваемого тела и приложены к каждой его частице. В частности, к объемным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных сил является сила, отнесенная к единице объема - кН/м3 .
Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рассматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на сосредоточенные и распределенные. К первым относятся нагрузки, реальная площадь приложения которых несоизмеримо меньше полной площади поверхности тела (например, воздействие колонн на фундаментную плиту достаточно больших размеров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Сосредоточенные усилия измеряются в кН, а распределенные - кН/м2.
Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия.
Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.
Рассмотрим тело, имеющее форму бруса (рис. 1.2, а).

|
Рис. 1.2
Пусть к нему приложена некоторая система внешних сил Р1, Р2, Р3,..., Рn , удовлетворяющая условиям равновесия, т.е. при действии указанных внешних сил тело находится в состоянии равновесия.
Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (PА ), действующей в сечении А (рис. 1.2, б).
Обозначая через Pлев и Рправ суммы внешних сил, приложенных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что
Pлев + Рправ = 0 (1.1)
для отсеченных частей бруса получим следующие очевидные соотношения:
Рлев + PA = 0; Рправ - PA = 0. (1.2)
Последние соотношения показывают, что равнодействующая внутренних сил РА в сечении А может определяться с равным успехом из условий равновесия либо левой, либо правой частей рассеченного тела. В этом суть метода сечений.
Внутренние усилия должны быть так распределены по сечению, чтобы деформированные поверхности сечения А при совмещении правой и левой частей тела в точности совпадали. Это требование в механике твердого деформируемого тела носит название условия неразрывности деформаций.
Воспользуемся правилами статики и приведем систему внутренних сил РА к центру тяжести сечения А в соответствии с правилами теоретической механики. В результате получим главный вектор сил  и главный вектор момента
и главный вектор момента 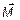 (рис. 1.3). Далее выбираем декартову систему координат xyz с началом координат, совпадающим с центром тяжести сечения А. Ось z направим по нормали к сечению, а оси x и y расположим в плоскости сечения. Спроектировав главный вектор сил
(рис. 1.3). Далее выбираем декартову систему координат xyz с началом координат, совпадающим с центром тяжести сечения А. Ось z направим по нормали к сечению, а оси x и y расположим в плоскости сечения. Спроектировав главный вектор сил  и главный момент
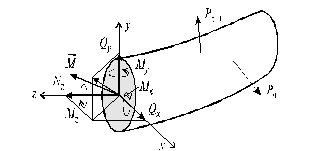
и главный момент 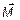 на координатные оси x, y, z, получаем шесть составляющих: три силы Nz , Qx , Qy и три момента Mz , Mx , My , называемых внутренними силовыми факторами в сечении бруса.
на координатные оси x, y, z, получаем шесть составляющих: три силы Nz , Qx , Qy и три момента Mz , Mx , My , называемых внутренними силовыми факторами в сечении бруса.
Составляющая Nz называется нормальной, или продольной силой в сечении. Силы Qx и Qy называются поперечными усилиями. Момент Mz называется крутящим моментом, а моменты Mx и My -изгибающими моментами относительно осей x и y, соответственно.
При известных внешних силах все шесть внутренних силовых
факторов в сечении определяются из шести уравнений равновесия,
которые могут быть составлены для отсеченной части.
Пусть R*, M* - результирующая сила и результирующий момент действующие на отсеченной части тела. Если тело при действии полной системы внешних сил находится в равновесном состоянии, то условия равновесия отсеченной части тела имеет вид:
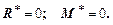 (1.3)
(1.3)
Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:
 (1.4)
(1.4)
которые в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: Qx, Qy, Nz, Mx, My, Mz.
Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.
В общем случае в сечении могут иметь место все шесть силовых факторов. Однако достаточно часто на практике встречаются случаи, когда некоторые внутренние усилия отсутствуют - такие виды нагружения бруса получили специальные названия (табл. 1).
|
Рис. 1.3
Сопротивления, при которых в поперечном сечении бруса действует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий сопротивление бруса называется сложным.
В заключение заметим, что при выполнении практических расчетов, для наглядности, как правило, определяются графики функций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изменения внутренних усилий вдоль продольной оси стержня называются эпюрами.
Таблица 1
Простейшие случаи сопротивления
| Вид напряженного состояния | Nz | Qx | Qy | Mz | Mx | My |
| Растяжение/сжатие | + | |||||
| Кручение | + | |||||
| Чистый изгиб относительно оси х | + | |||||
| Чистый изгиб относительно оси у | + | |||||
| Поперечный изгиб относительно оси х | + | + | ||||
| Поперечный изгиб относительно оси у | + | + |
Примечание: + означает наличие усилия, 0 - его отсутствие.
Напряжение – интенсивность распределения величины внутреннего усилия по площади поперечного сечения.
В окрестности произвольной точки К, принадлежащей сечению А некоторого нагруженного тела, выделим элементарную площадку DF, в пределах которой действует внутреннее усилие D  (рис. 1.4, а). Векторная величина
(рис. 1.4, а). Векторная величина
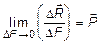 (1.5)
(1.5)
называется полным напряжением в точке К. Проекция вектора полного напряжения 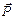 на нормаль к данной площадке обозначается через s и называется нормальным напряжением.
на нормаль к данной площадке обозначается через s и называется нормальным напряжением.
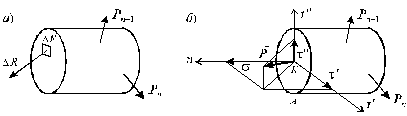
|
Рис. 1.4
Проекции вектора 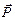 на перпендикулярные оси в плоскости площадки (рис. 1.4, б) называются касательными напряжениями по направлению соответствующих осей и обозначаются t´ и t´´. Если через ту же самую точку К провести другую площадку, то, в общем случае будем иметь другое полное напряжение. Совокупность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.
на перпендикулярные оси в плоскости площадки (рис. 1.4, б) называются касательными напряжениями по направлению соответствующих осей и обозначаются t´ и t´´. Если через ту же самую точку К провести другую площадку, то, в общем случае будем иметь другое полное напряжение. Совокупность напряжений для множества площадок, проходящих через данную точку, образует напряженное состояние в этой точке.
| <== предыдущая страница | | | следующая страница ==> |
| Модели прочностной надежности | | | Перемещения и деформации. Под действием внешних сил твердые тела изменяют свою геометрическую форму, а точки тела неодинаково перемещаются в пространстве |
Дата добавления: 2014-11-06; просмотров: 719; Нарушение авторских прав

Мы поможем в написании ваших работ!