Метод резолюций в логике предикатов

Для того чтобы метод резолюций можно было применить к предложениям логики предикатов, необходимо вначале преодолеть различие одноименных предикатных символов, порожденное различием термов, выступающих в роли аргументов этих предикатов. Поэтому метод резолюций в логике предикатов включает шаги:

Множество утверждений естественного языка записывается в виде формул логики предикатов.

Каждая из записанных формул преобразуется к пренексной нормальной форме.

Выполняется переход каждой формулы к сколемовской нормальной форме. При необходимости производится нормализация переменных.

Полученные формулы записываются в теоретико-множественной форме.

К полученному множеству дизъюнктов применяется алгоритм унификации и определяется НОУ, если это возможно. После унификации дизъюнкты, входящие в каждое предложение, содержат только основные примеры.

Алгоритм резолюции применяется к полученному множеству основных примеров. Два дизъюнкта могут резольвировать, если они содержат дополнительные литералы (атомы, различающиеся способом вхождения в дизъюнкт).

Пусть имеются два дизъюнкта (P1ÚP2Ú…ÚPn) и ( 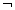P1ÚQ2Ú…ÚQm). Считаем, что все Pi и Qj различны. Дизъюнкты содержат дополнительные литералыР1 и ØР1. Как и в логике высказываний, такие два дизъюнкта резольвируют, порождая новый дизъюнкт (P2Ú…ÚPnÚQ2Ú…ÚQm), в котором участвуют все литералы обоих дизъюнктов, кроме P1 и ØР1. Новый дизъюнкт называется резольвентой и несет новое знание, которое добавляется к имеющимся фактам (дизъюнктам).

Таким образом, метод резолюций в логике предикатов является расширением метода резолюций в логике высказываний за счет добавления алгоритма унификации, применяемого для идентификации одноименных атомов. Для множества S дизъюнктов логики предикатов резолютивный вывод из S есть конечная последовательность дизъюнктов C1, …, Cn, такая, что для каждого Ci, либо CiÎS, либо CiÎ{R(Cj,Ck) | "j"k(1£j, k£n)}, т.е. является резольвентой дизъюнктов Cj и Ck.

Поскольку переменные во всех дизъюнктах считаются связанными кванторами общности, можно переименовывать эти переменные, чтобы избежать конфликтов во время процедуры унификации. Такое переименование называется нормализацией переменных.

Основные частные случаи резолюции приведены в табл. 12. Из таблицы видно, что резолюция позволяет объединить несколько операций в одно простое правило вывода.

Таблица 12 Предложения и резольвенты

Родительские дизъюнкты	Резольвенты	Комментарии
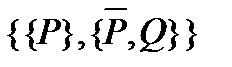
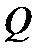
		Modus Ponens
		Предложение Q Ú Q «сворачивается» в Q. Эта резольвента называется слиянием
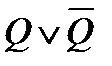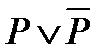
	и	Здесь две возможные резольвенты; в данном случае обе являются тавтологиями
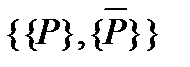
		Пустое предложение, является признаком противоречия
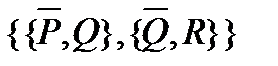
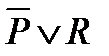	(т.е. P®R)	Цепочка

Примеры

1. Из двух данных дизъюнктов

C₁=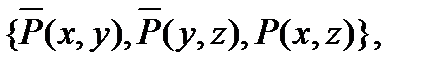

C₂=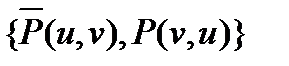

требуется получить резольвенту

C₃=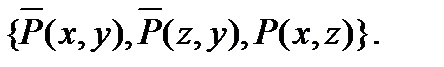

Рассмотрим приведенные дизъюнкты как утверждения о следовании некоторых фактов из других фактов. Приведенным дизъюнктам соответствуют формулы логики предикатов:

для С1

;

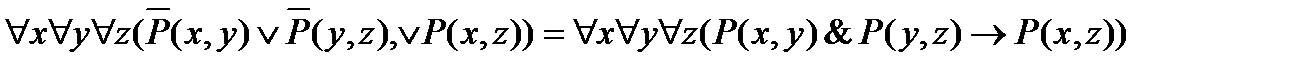для С2

;

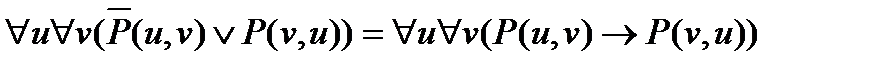для С3

.

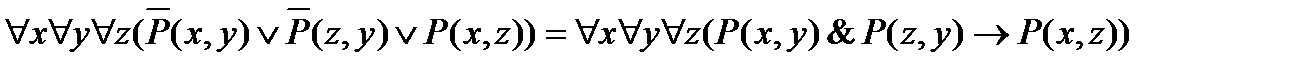Построим вывод дизъюнкта С3 методом резолюций.

(1)	C1	Исходные дизъюнкты
(2)	C2
(3)		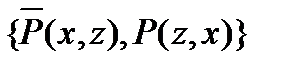Из (2), подстановка {u/x, v/z}, нормализация переменных.
(4)		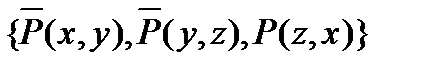Резолюция (1) и (3).
(5)		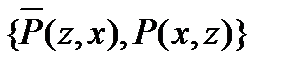Из (2), подстановка {u/z, v/x}, нормализация переменных.
(6)		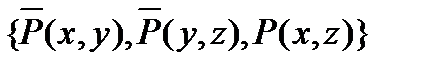Резолюция (4) и (5).
(7)		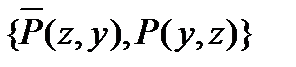Из (2), подстановка {u/z, v/y}, нормализация переменных.
(8)	C3	резолюция (6) и (7).

2. Допустим, существуют факты:

F1: Все люди смертны. Это можно представить секвенцией ├(Все люди смертны), которая называется фактом.

F2: Сократ - человек. Этой формуле соответствует факт ├(Сократ – человек).

Требуется проверить вывод Сократ смертен.

Представим эти предложения в виде формул:

F1: "х (человек(х)®смертен(х)),

F2: человек(Сократ)

R: смертен (Сократ)

Поскольку в методе резолюций доказательство строится методом от противного, в представленное рассуждение необходимо внести противоречие, которое приведет к невыполнимости этого рассуждения. Обычно такое противоречие вводится путем опровержения вывода. С учетом этого запишем полученные формулы в виде бескванторных формул, представленных в КНФ.

F1: (Øчеловек(x)Úсмертен(x));

F2: человек(Сократ);

F3: (Øсмертен(Сократ)).

Последней формулой введено противоречие в исходное рассуждение.

Теоретико-множественное представление сформулированной таким образом задачи имеет вид:

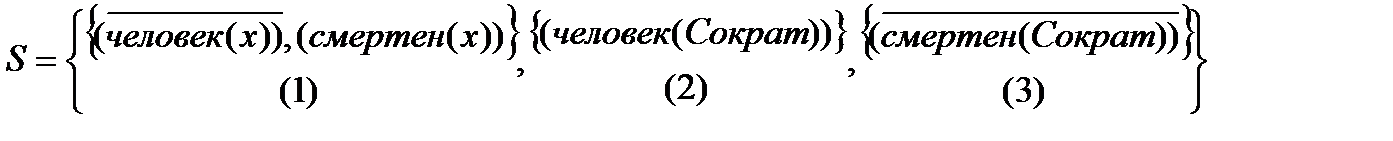
Применяя метод унификации к множеству S, определим НОУ. Для атома человек(x) из дизъюнктов (1) и (2) получаем подстановку q={x/Сократ}. Для дизъюнктов (1) и (3) имеем ту же подстановку. Применяя полученный НОУ к S, получим

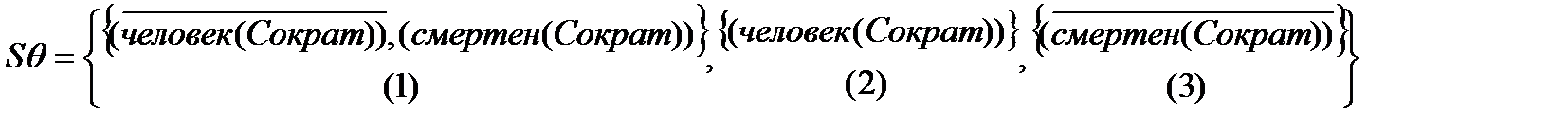Резольвента дизъюнктов (1) и (2) имеет вид

R(1,2)=F4: {(смертен(Сократ))}.

Применяя далее резолюцию к дизъюнктам (3) и (4), получим пустую резольвенту

R(3,4) = F5: ð.

Введя опровержение вывода силлогизма, получили противоречие, признаком которого является пустая резольвента. Следовательно, неверно, что Сократ бессмертен.

Пример. Докажем справедливость следующего рассуждения:

Посылки:

F1: Некоторые пациенты любят докторов.

F2: Ни один пациент не любит знахарей.

Заключение:

R: Никакой доктор не является знахарем.

¨ Введем элементарные высказывания:

P(x): “x – пациент”;

D(x): “x – доктор”;

Z(x): “x – знахарь”;

L(x,y): “x любит y”.

Запишем рассуждения естественного языка, сформулированные в условии, с помощью формул логики предикатов:

F1: $xP(x),

F2:$xD(x),

F3:$xZ(x),

F4: $x"y(P(x)&D(y)®L(x,y)),

,

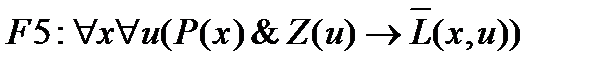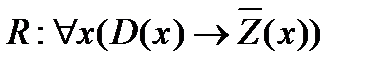- утверждение, которое следует доказать.

Так как доказательство строится от противного, сформулируем отрицание утверждения R:

Следующий этап – приведение всех формул к пренексной нормальной форме, но вначале произведем нормализацию переменных. Так как переменная x имеет в разных формулах разный смысл, то во избежание коллизии переменных целесообразно переименовать некоторые из связанных переменных. Примем следующие назначения переменных: x – пациент, y –доктор, u – знахарь, – и перепишем формулы F1-F6 в пренексной нормальной форме:

F1:$xP(x),

F2:$yD(y),

F3:$uZ(u),

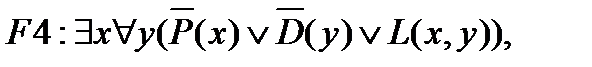
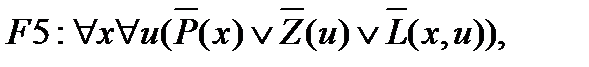
F6:$y(D(y)&Z(y)).

Переходя к сколемовской нормальной форме, введем сколемовские константы: с – для пациента, а – для доктора, b – для знахаря. Тогда теоретико-множественное представление приведенного рассуждения будет иметь вид

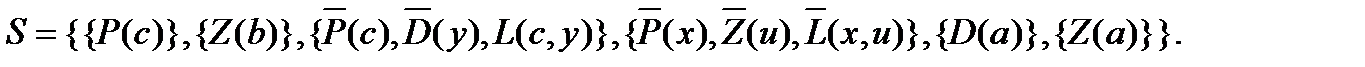
Применим к этому множеству алгоритм унификации. В языке логического программирования ПРОЛОГ применяется эффективный алгоритм доказательства противоречивости множества дизъюнктов, который состоит в том, что вначале и для унификации, и для резолюции выбираются целевые дизъюнкты. В рассматриваемом примере это дизъюнкты, соответствующие формуле F6, т.е. {D(a)}, {Z(a)}. Выбрав дизъюнкт {D(a)}, найдем все встречающиеся в множестве S дизъюнкты, содержащие атом D, найдем множество рассогласования DS1={y,a}. Проверка вхождений дает отрицательный ответ. Следовательно, подстановка, унифицирующая атомы D, имеет вид q1={y/a}. Применяя эту подстановку к S, получим

.

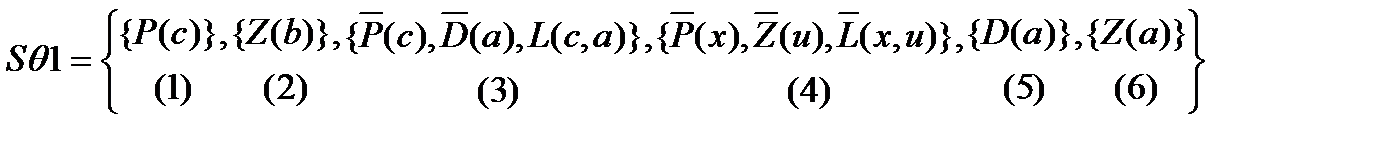Следующий подлежащий унификации атом - Р(1). Для него определяем подстановку q2={x/c}. После выполнения этой подстановки, которую мы здесь опустим, останется не унифицированным атом L(2). Для него унифицирующая подстановка q3={u/a}.

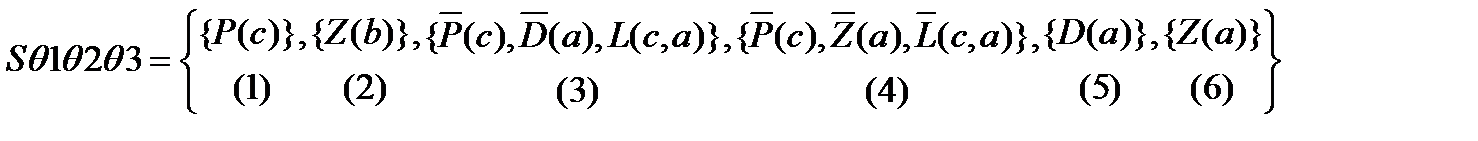Наиболее общий унификатор является объединением трех полученных унификаторов и имеет вид

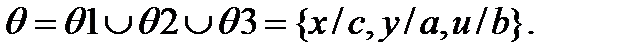
К полученному множеству основных примеров можно применять метод резолюции, как это делалось в логике высказываний. Целью в данном рассуждении являются дизъюнкты (5) и (6). Выберем для резолюции дизъюнкты (3) и (5).

R(3,5)=C7=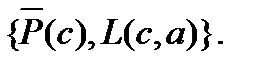

Далее будем выбирать подходящие дизъюнкты с целью получения пустого дизъюнкта, подтверждающего рассуждение:

R(4,6)=C8=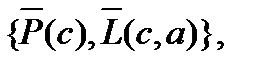

.

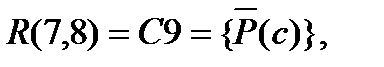
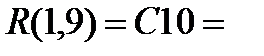Получение пустого дизъюнкта означает, что в рассмотренном наборе фактов имеется противоречие, которое возникло из-за введения отрицания в заключение. Следовательно, заключение рассуждения верно.

Дата добавления: 2014-11-08; просмотров: 1539; Нарушение авторских прав

Мы поможем в написании ваших работ!