
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Элементы механики твердого тела
Как было сказано выше, движение любого тела можно представить как наложение поступательного и вращательного движения. При поступательном движении все точки тела совершают за один и тот же промежуток времени одинаковые перемещения, вследствие чего ускорения и скорости в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, центра масс) для того, чтобы полностью охарактеризовать движение тела. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой (оси вращения). Для описания вращательного движения нужно задать положение оси в пространстве и угловую скорость в каждый момент времени.
Рассмотрим вращательное движение и связанные с ним характеристики более подробно. Вначале введем понятие момента силы. Повседневный опыт показывает, что при вращении какого-либо тела с помощью рычага, существенным оказывается не только модуль силы, но и длина рычага. В соответствии с этим вводится понятие момента силы.
Моментом силы относительно неподвижной точки О называется векторная величина (псевдовектор) определяемая произведением
 , где
, где  - радиус-вектор, проведенный из точки О до точки приложения силы, α –угол между
- радиус-вектор, проведенный из точки О до точки приложения силы, α –угол между  и
и  .
.

Момент силы называют также вращающим моментом.
По аналогии с моментом силы введем понятие момента импульса материальной точки относительно неподвижной точки О :
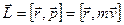 , где
, где  -радиус-вектор, определяющий положение частицы относительно т.О,
-радиус-вектор, определяющий положение частицы относительно т.О,  - импульс частицы.
- импульс частицы.
Моментом импульса системы относительно точки О называют векторную сумму моментов импульсов частиц, входящих в систему:
 .
.
Направление  совпадает с направлением поступательного движения правого винта при его вращении от
совпадает с направлением поступательного движения правого винта при его вращении от  к
к 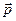 .
.

Если частица движется по окружности радиуса R, то момент импульса L относительно центра окружности по модулю равен  . Так как радиус окружности R=const, то L может изменяться только за счет модуля скорости.
. Так как радиус окружности R=const, то L может изменяться только за счет модуля скорости.
При равномерном прямолинейном движении и при движении по окружности с постоянной скоростью  момент импульса L остается постоянным по модулю и направлению.
момент импульса L остается постоянным по модулю и направлению.
Выясним, от чего зависит изменение момента импульса материальной точки? Для этого продифференцируем  .
.
 .
.
 ,
,  ,
,  . Тогда
. Тогда
 , т.е.
, т.е.  .
.
Получили, что скорость изменения момента импульса во времени равна суммарному моменту сил, действующих на частицу.
Рассмотрим систему частиц, на которые действуют внутренние и внешние силы. Моментом импульса L системы относительно т.О называется сумма моментов импульса отдельных частиц  .
.
Продифференцируем по времени  . Но в соответствии с
. Но в соответствии с  , для каждой частицы запишем
, для каждой частицы запишем 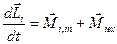 , где в правой части равенства сумма моментов внутренних сил действующих на i-тую частицу и сумма моментов внешних сил действующих на i-тую частицу.
, где в правой части равенства сумма моментов внутренних сил действующих на i-тую частицу и сумма моментов внешних сил действующих на i-тую частицу.
Для системы 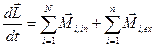 .
.
Моменты внутренних сил попарно уравновешивают друг друга и сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю:
 ,
,
но  по третьему закону Ньютона и
по третьему закону Ньютона и
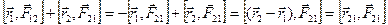 ,
,
|
| |
 Это значит, что
Это значит, что  , т.е. момент импульса замкнутой системы материальных точек остается неизменным.
, т.е. момент импульса замкнутой системы материальных точек остается неизменным.
В основе закона сохранения момента импульса лежит изотропия пространства, т.е. одинаковость свойств пространства по всем направлениям. Поворот замкнутой системы частиц без изменения конфигурации и относительных скоростей не изменяет свойства системы.
Возьмем на оси вращения точку О и будем характеризовать положение образующих тело частиц с помощью радиус-векторов  , проведенных из т.О. Момент импульса i-той частицы:
, проведенных из т.О. Момент импульса i-той частицы:

Величина, равная сумме произведений элементарных масс на квадраты их расстояния до оси вращения называется моментом инерции тела относительно оси:  .
.
В этих обозначениях получаем 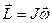 . Полученная формула аналогична
. Полученная формула аналогична  . Роль массы играет момент инерции, вместо линейной скорости – угловая скорость. Иначе – мерой инертности тела при вращательном движении является момент инерции тела.
. Роль массы играет момент инерции, вместо линейной скорости – угловая скорость. Иначе – мерой инертности тела при вращательном движении является момент инерции тела.
Из формулы 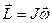 видно, что величина момента импульса не зависит от того, относительно какой точки О на оси вращения берется
видно, что величина момента импульса не зависит от того, относительно какой точки О на оси вращения берется  . Согласно формуле
. Согласно формуле  или
или  ,
,  (1) - это основное уравнение динамики вращательного движения.
(1) - это основное уравнение динамики вращательного движения.
Уравнение (1) – есть аналог второго закона Ньютона (  ). Роль массы играет момент инерции, роль линейного ускорения – угловое ускорение, роль результирующей силы – суммарный момент внешних сил.
). Роль массы играет момент инерции, роль линейного ускорения – угловое ускорение, роль результирующей силы – суммарный момент внешних сил.
| <== предыдущая страница | | | следующая страница ==> |
| Правила определения | | | Момент инерции тела. Физическая величина, численно равная сумме произведений масс материальных точек системы на квадраты их расстояния до рассматриваемой оси |
Дата добавления: 2014-11-08; просмотров: 590; Нарушение авторских прав

Мы поможем в написании ваших работ!
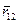 и
и 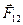 параллельны и одинаково направлены, поэтому
параллельны и одинаково направлены, поэтому  и
и  .
Мы приходим к уравнению
.
Мы приходим к уравнению  и
и  , то
, то 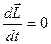 .
.