
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ТЕМА: «ОРГАНИЗАЦИЯ ДАННЫХ В МНОЖЕСТВА»
1. Понятие и определение множества в теории множеств.
Множества являются основополагающими структурами в математике и программировании и часто используются при проектировании алгоритмов и программ с целью повышения их эффективности.
В математике множество – это любой набор объектов, который понимается как единое целое. Объекты, принадлежащие множеству, называются членами или элементами множества. Множество определяется только своими элементами, элементы множества неупорядочены, и два множества равны тогда и только тогда, когда они содержат одни и те же элементы. Например, следующие множества одинаковы: {1,3,5}, {3,1,5}, {5,3,1} и т.д.
Если все элементы одного множества являются также элементами другого, но не наоборот, то первое множество называется подмножеством второго, например множество {1,3} является подмножеством {1,3,5}. Множество всех подмножеств данного множества называется его множеством-степенью. Множество-степень {1,3,5} есть {{1,3,5}, {1,3}, {1,5}, {3,5}, {1}, {3}, {5}, {}}. Т.к. каждый элемент исходного множества {1,3,5} или присутствует, или отсутствует в каждом из подмножеств, общее число подмножеств есть 23 = 8.
Над подмножествами определены три бинарные операции, похожие на операции сложения, умножения и вычитания для целых чисел.
Объединение 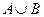 (сумма) двух множеств А и В – это множество, элементы которого являются элементами либо А, либо В. например, объединение множеств {1} и {3,5} является множество {1,3,5}.
(сумма) двух множеств А и В – это множество, элементы которого являются элементами либо А, либо В. например, объединение множеств {1} и {3,5} является множество {1,3,5}.
Пересечение 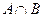 (произведение) двух множеств А и В – это множество, элементы которого являются элементами как А, так и В. Например, пересечением множеств {1,3,5} и {3,5,7} является множество {3,5}.
(произведение) двух множеств А и В – это множество, элементы которого являются элементами как А, так и В. Например, пересечением множеств {1,3,5} и {3,5,7} является множество {3,5}.
Дополнением В\A (разность) А до В – это множество, элементы которого являются элементами множества В, но не являются элементами множества А. Например, множество {1,3} является дополнением множества {5} до {1,3,5}.
2. Понятие и обозначение множества в Паскале.
В Паскале допускаются только конечные множества, причем все элементы множества должны быть значениями одного типа. Максимально допустимое число элементов множества определяется конкретной реализацией языка, в Турбо Паскале – это 256. Для элементов множества может использоваться тип, область допустимых значений которого меньше указанного числа. Введенное ограничение, с одной стороны, упрощает язык, а с другой – позволяет эффективно реализовывать множества.
В Паскале множество – это структура данных, представляющая ограниченную неупорядоченную совокупность различных элементов одного типа. Тип, к которому должны принадлежать все члены множества, называется базовым типом множества. В качестве базового типа множеств может использоваться любой скалярный порядковый тип, кроме word, integer, longint.
Для определения значения множеств используется конструктор множества, представляющий собой список элементов множества, заключенный в квадратные скобки. Элементы множества могут задаваться константами, переменными и выражениями базового типа. Множество может вообще не иметь элементов, т.е. быть пустым. Например:
- [ ] – пустое множество;
- [2, 4, 7] – множество из трех элементов целого типа;
- [‘a’, ’s’, ’d’] – множество из трех элементов символьного типа;
- [red, yellow, green] – множество из трех элементов перечисляемого типа;
- [1, k, 2*k] – множество из трех элементов целого типа: константы 1, текущего значения переменной k и значения выражения 2*k.
Если список элементов, образующих множество, упорядочен в соответствии с заданным базовым типом, то можно не перечислять все элементы, а указать диапазон значений:
- [1..100] – множество из 100 целых чисел;
- [k..2*k] – множество целых чисел от значения k до значения 2*k;
- [‘a’..’d’, ’f’..’h’, ‘k’] – множество значений символьного типа, состоящее из элементов a, b, c, d, f, g, h, k;
- [1..1, 5..1] эквивалентно [1];
- [‘d’..’a’] эквивалентно [ ].
Порядок перечисления элементов в множестве не играет роли, поэтому
- [false, true] эквивалентно [true, false];
- [1, 3, 5] эквивалентно [5, 3, 1];
- [1, k, 2*k] эквивалентно [1, 2] при k=1.
Конструктор множества можно рассматривать как операцию образования значения множественного типа из множества значений базового типа.
3. Определение множественного типа.
Для использования в Паскаль-программах таких структур данных, как множества, в язык введено понятие множественного типа. Значением множественного типа является множество. Как и любой тип в Паскале, множественный тип определяет область допустимых значений, относящихся к этому типу, и операции, применимые к этим значениям. Область допустимых значений множественного типа есть множество-степень базового типа. В общем виде описание множественного типа реализуется следующей конструкцией:
type <имя_типа> = set of <базовый_тип>;
В качестве базового типа, из значений которого создаются конкретные значения множественного типа – множества, может быть использован допустимый стандартный тип, либо тип, ранее определенный пользователем. Например:
type letter = ‘a’..’z’; {базовый тип}
setoflettres = set of letter;
Тип setoflettres включает в себя все возможные подмножества элементов базового типа – буквы от a до z, а также пустое множество.
Если базовый тип содержит k значений, то множественный тип определяет 2k подмножеств, относящихся к значениям данного множественного типа, в том числе пустое множество. Например, множественный тип set of 1..3, определяет область из 23 подмножеств: [ ], [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3]. А множественный тип set of boolean, определяет область из 22 подмножеств: [ ], [false], [true], [false, true].
Если в программу введен множественный тип, то могут быть объявлены и использованы переменные и типизированные константы множественного типа. Например:
var gllettres: setoflettres;
A, B, C: setoflettres;
begin
. . .
glletters:=[‘a’,’e’,’I’,’o’,’u’];
A:=[‘i’,’j’,’r’,’l’,’m’,’n’];
B:=A;
C:=[ ];
При введении типизированных констант-множеств их начальные значения задаются с помощью конструктора множества:
type ten=set of 0..9;
number=set of ‘0’..’9’;
const index: ten=[0,2,4,6,8];
digit: number=[‘0’..’9’];
begin
. . .
digit:=[‘1’,’3’,’5’,’7’,’9’];
Переменные и типизированные константы множественного типа могут участвовать в операторах присваивания слева и справа от знака присваивания, если они принадлежат к идентичным типам.
4. Операции над множествами.
К переменным и константам множественного типа в Паскале применимы операции «+» - объединение; «*» - пересечение (умножение); «-» - разность.
Объединением (суммой) двух и более множеств называется множество, состоящее из элементов, входящих хотя бы в одно из исходных множеств. Например:
[1, 3, 5] + [3, 7, 9] = [1, 3, 5, 7, 9].
Пересечением (умножением) двух и более множеств называется множество, состоящее из элементов, входящих хотя бы в одно из исходных множеств. Например:
[0, 2, 4, 6] * [2, 4, 8] = [2, 4].
Пересечение множеств может быть пустым:
[1, 3, 5, 7, 9] * [0, 2, 4, 6, 8] = [ ].
Разностью между множеством В и множеством А называется множество элементов из В, не являющихся элементами из А. Например:
[0 .. 9] – [1, 3, 5, 7, 9] = [0, 2, 4, 6, 8].
Над множествами в Паскале определены также следующие операции отношения:
| A = B | тождественность множеств (в математике  ) )
|
| A <> B | нетождественность множеств (в математике 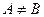 ) )
|
| A <= B | А содержится в В (в математике  ) )
|
| A >= B | А содержит В (в математике 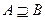 ) )
|
Например, отношение
| [0] = [ ] | имеет значение false |
| [0, 2, 4, 6, 8] = [8, 6, 4, 2, 0] | имеет значение true |
| [0] <= [0, 2, 4, 6, 8] | имеет значение true |
| [0, 2, 4, 6, 8] >= [1, 3] | имеет значение false |
Операция отношения x in A проверяет принадлежность элемента базового типа x множеству А (в математике 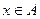 ). Например, если описано множество
). Например, если описано множество
const A: set of 50..53 = [50..53];
то отношение 50 in А имеет значение true, а отношение 50 in [51..53] имеет значение false.
Введенные операции над множествами позволяют строить некоторые выражения для получения новых множественных значений. При вычислении значений множественных выражений действует установленное правило приоритета операций: операции объединения и разности множеств относятся к операциям типа сложения и имеют тот же приоритет, что и все остальные операции типа сложения; операция пересечения множеств относится к операциям типа умножения; все операции отношения имеют наименьший приоритет. Например, значение выражения
| [1, 2, 5, 6, 7] * [2..6] + [3, 9] | равно [2, 3, 5, 6, 9] |
| ([3, 4, 5] + [1, 3, 6, 7]) * [5..7] – [6] | равно [5, 7] |
| (7 in [1, 3, 5, 7, 9]) and ([7] <= [1, 3, 5, 7, 9]) | равно true |
5. Использование множеств в программах.
Принятая в вычислительной технике двоичная форма представления информации позволяет эффективно реализовать как представление в памяти самих множеств, так и выполнение операций над ними. Множество в Паскале имеет внутреннее представление в виде строки битов, где каждый элемент базового типа множества представлен одним битом: отсутствие элемента в множестве обозначается нулем, а его присутствие – единицей. Например, пусть задана переменная множественного типа
var h: set of [red, yellow, green, blue];
Тогда значение этой переменной, равное
[red, yellow, green, blue], представлено битовой строкой ‘1111’;
[red, yellow, green], представлено битовой строкой ‘1110’;
[red, yellow], представлено битовой строкой ‘1100’;
[yellow], представлено битовой строкой ‘0100’.
В конкретных реализациях размер множества обычно ограничен размером одного или нескольких машинных слов (в Турбо Паскале размер множества не может превышать 256 элементов). Поэтому в качестве базового типа множества может использоваться только порядковый тип, область допустимых значений которого меньше указанного числа, и к элементам множества применимы функции ORD, SUCC, PRED, определяющие их расположение в упорядоченном множестве значений базового типа.
Представление значений множественного типа битовыми строками дает возможность операции над множествами свести к операциям над битовыми строками, которые выполняются относительно быстро, поэтому действия с множествами часто используют для исключения более сложных логических условий. Например, вместо проверки сложного выражения
(ch = ‘a’) or (ch = ‘e’) or (ch = ‘i’) or (ch = ‘o’) or (ch = ‘u’) or (ch = ‘y’)
можно написать более простое и понятное:
ch in [‘a’, ‘e’, ‘i’, ‘o’, ‘u’, ‘y’].
6. Индивидуальные задания.
| № варианта | З А Д А Н И Е |
| 1. | Вычислить сумму тех элементов матрицы А, номера строк и столбцов которых принадлежат к заданным множествам целых чисел S1 и S2. |
| 2. | Дан текст из цифр и латинских букв. Определить, каких букв – гласных (a, e, i, o, u, y) или согласных – больше в этом тексте. |
| 3. | Вывести в возрастающем порядке все цифры, входящие в десятичную запись некоторого натурального числа n. |
| 4. | Вывести в возрастающем порядке все цифры, не входящие в десятичную запись некоторого натурального числа n. |
| 5. | Дан текст, состоящий из латинских букв. Вывести все буквы, входящие в текст не менее двух раз. |
| 6. | Дан текст, состоящий из латинских букв. Вывести все буквы, входящие в текст по одному разу. |
| 7. | Дано предложение, состоящее из латинских букв. Вывести все согласные буквы, входящие в это предложение. |
| 8. | Вывести в возрастающем порядке все целые числа из диапазона 1 .. 1000, представимые в виде n2+m2, где n, m > 0. |
| 9. | В некотором районе города находятся 5 продовольственных магазинов. В каждый из них завезли некоторые продукты из тех, что есть на базе: хлеб, масло, молоко, мясо, рыба, соль, сыр, сахар, чай, кофе, творог, мука. Определить, какие продукты есть во всех магазинах; какие – хотя бы в одном; каких нет нигде. |
| 10. | Дано предложение, состоящее из латинских букв. Вывести все согласные буквы, которые входят хотя бы в одно слово. |
| 11. | Дано предложение, состоящее из латинских букв. Вывести все согласные буквы, которые входят только в одно слово. |
| 12. | Несколько городов одного региона обслуживает одно автотранспортное предприятие, наладившее между ними автобусные сообщения. Каждый автобус за один рейс заходит в некоторые из этих городов. Всего 5-10 рейсов. Составить программу, которая отвечала бы на вопросы: в какие города можно добраться на автобусе за один рейс, какими рейсами можно добраться из города А в город В? |
| 13. | Дано предложение, состоящее из латинских букв. Вывести все гласные буквы, которые не входят более чем в одно слово. |
| 14. | Введите символьное множество. Разбейте его на три подмножества: цифры; буквы; специальные символы. Проверьте, есть ли среди них пустое множество. |
| 15. | В тексте определить и вывести повторяющиеся гласные буквы. |
| 16. | В группе есть студенты, увлекающиеся спортом, и студенты, увлекающиеся искусством. Определить множество студентов группы, увлекающихся и спортом и искусством. |
| 17. | В группе есть студенты, увлекающиеся спортом, и студенты, увлекающиеся искусством. Определить множество студентов группы, которые не увлекаются ни спортом, ни искусством. |
| 18. | В группе есть студенты, увлекающиеся спортом, и студенты, увлекающиеся искусством. Определить множество студентов группы, которые увлекаются либо спортом, либо искусством. |
| 19. | Множество S состоит из букв, которые содержатся хотя бы в одном из слов Киев, Днепропетровск, Запорожье, Севастополь. Определить, можно ли из множества S составить слово Харьков. |
| 20. | В заданном тексте из букв латинского алфавита определить общее число вхождение в него букв a, e, c, h. |
| 21. | Вывести в убывающем порядке все нечетные простые числа из максимально допустимого диапазона. |
| 22. | Вывести в убывающем порядке все четные простые числа из максимально допустимого диапазона. |
| 23. | Написать программу, формирующую случайным образом множество целых чисел и осуществляющую вывод элементов этого множества. |
| 24. | Написать программу, формирующую случайным образом множество целых чисел и осуществляющую вывод элементов этого множества. |
| 25. | Написать программу, формирующую случайным образом два числовых множества и определяющую, в каком отношении находятся эти множества. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каким образом описывается множественный тип в программе?
2. Что определяет множественный тип (какова область допустимых значений множественного типа)?
3. Какие операции определены над данными множественного типа?
4. Что является пересечением множеств?
5. Что является объединением множеств?
6. Что является дополнением множеств?
7. Какие операции отношения определены над множествами?
8. Каково внутренне представление значений множественного типа?
9. Что такое множество-константа и что такое множество-переменная?
10. Какие объекты можно описывать множественным типом?
| <== предыдущая страница | | | следующая страница ==> |
| Типичные ошибки в политической рекламе | | | ИЗМЕРЕНИЕ ДАВЛЕНИЯ |
Дата добавления: 2014-11-14; просмотров: 416; Нарушение авторских прав

Мы поможем в написании ваших работ!