ПОЛНЫЕ СИСТЕМЫ БУЛЕВСКИХ ФУНКЦИЙ

Пусть B Í P₂.

ОПРЕДЕЛЕНИЕ

Замыканием множества B называется множество, которое обозначается как [B], состоящее из всех таких функций, представимых формулами над B.

То есть [B] состоит из всех таких булевских функций, которые могут быть представлены формулами, составленными из функций, множества B. Например, если B = {x₁ + x₂, 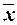}, то[B] состоит из функций, представляющих либо суммы переменных со свободным членом, равным 1, либо такие суммы без свободного члена, либо нуль.

Действительно, так как 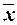= x + 1, то, раскрывая скобки в произвольной формуле U над B и удаляя из полученной суммы пары одинаковых слагаемых (по правилу x + x = 0), можно получить либо сумму указанного вида, либо пустую запись, когда сумма равна 0. В последнем случае формула записывается как 0.

Множество [B] для рассмотренного примера называется классом линейных функций.

Легко проверяются следующие свойства замыкания, справедливые для любых множеств функций в P₂:

1) [[B]] = [B];

2) B₁ Í B₂ Þ [B₁] Í [B₂];

3) [B₁ Ç B₂] Í [B₁] Ç [B₂];

4) [B₁ È B₂ ] Ê [B₁] È [B₂];

5) B Í [B₁].

Упражнение

1.Описать замыкания следующих классов булевских функций:

a) {x₁& x₂}, }; b) {{x₁ & x₂, x₁ Ú x₂}; c) { }.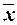

2. Привести примеры таких множеств B₁ и B₂, для которых в соотношениях 1) – 4) имеют место строгие включения.

ОПРЕДЕЛЕНИЕ

Множество B Í P₂ называется полной системой, если
[B] = P₂.

Один пример полной системы в данной главе уже рассматривался. Поскольку всякая булевская функция представляется формулой над множеством функций
B = {x₁& x₂, x₁Ú x₂, 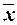}, то [B] = P₂, а значит, система B является полной.

Другим примером полной системы является все множество булевских функций P₂.

Определение полноты произвольной системы функций, осуществляемое в соответствии с определением полноты, предполагает доказательство возможности выражения всякой б.ф. через функции полной системы. Такой процесс можно упростить, если воспользоваться следующей теоремой.

ТЕОРЕМА 4.4 (теорема редукции)

Пусть B₁ и B₂ - некоторые системы булевых функций, для которых выполнены условия:

1) [B₁] = P₂;

2) " f Î B₁ (f Î [B₂]).

Тогда B₂ является полной системой, т.е. если всякая функция некоторой полной системы выражается через функции другой системы, то другая система также является полной.

Доказательство

Пусть h(x₁, . . ., x_n) - произвольная булевская функция. Покажем, что h Î [B₂]. Из этого будет следовать, что [B₂] = P₂.

Из полноты системы функций B₁ следует, что существует формула U(f₁, . . . , f_k) над B₁, которая представляет функцию h.

Здесь f₁, . . . , f_k - все различные функции из B₁, которые входят в запись формулы U.

Из свойства 2 условий теоремы следует, что каждая функция f_i Î B₁ представляется некоторой формулой над множеством B₂. Возьмем произвольные такие формулы и обозначим их как U_i, i = 1, . . . , k.

В формуле U произведем однократную замену каждого вхождения функций f₁ , . . . , f_k на соответствующие им формулы
U₁, . . . , U_k. В результате получим формулу W, являющуюся формулой над B₂.

По теореме о замене равных справедливо соотношение
U º W. Следовательно, W представляет h. Поскольку h - это произвольная булевская функция, то B₂ является полной системой.

Доказательство окончено.

Используя данную теорему можно установить полноту произвольной системы B, выразив через функции этой системы все функции некоторой уже известной полной системы. Например, это может быть {x₁& x₂, x₁Ú x₂, }.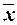

Рассмотрим несколько примеров.

1. B = {x₁& x₂, 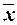}. Поскольку x₁& x₂ и 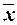содержатся в B, то для доказательства полноты этой системы достаточно выразить функцию 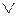через функции & и .

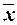Такое представление можно получить с помощью соотношения Де-Моргана 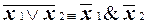. Поэтому 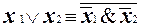, т.е. [B] = P₂.

2. B = {x₁Ú x₂, 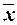}. Аналогично предыдущему случаю можно показать, что 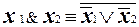. Такое представление, получается из второго соотношения Де-Моргана, т.е. B также является полной системой.

3. Пусть B = 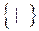. Напомним, что | называется функцией Шеффера и соответствует отрицанию конъюнкции x₁| x₂ º ( 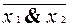). Тогда нетрудно проверить, что x | x º 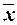, а (x₁| x₂) | (x₁| x₂) º x₁ & x₂.

Поэтому функция Шеффера образует полную систему.

Для доказательства неполноты произвольной системы B в некоторых случаях можно воспользоваться следующим методом, в котором:

1) выделяется специальное свойство, которым обладают все функции системы, но не обладают все булевы функции;

2) доказывается, что функции, представляемые формулами над B, также обладают выделенным свойством.

Тогда система B является неполной, поскольку существуют функции, имеющие свойство, которым не обладает ни одна функция из [B].

Пример. Рассмотрим систему B = {x₁+ 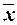₂, x }.

1. Нетрудно проверить, что обе функции из B на единичных наборах значений переменных равны 1 и этим свойством не обладает функция Шеффера.

2. Всякая формула над B представляет б.ф., которая на единичном наборе значений переменных принимает значение 1.

Следовательно, множество B не является полной системой.

Дата добавления: 2014-11-15; просмотров: 380; Нарушение авторских прав

Мы поможем в написании ваших работ!