Синтез линейных систем управления

Основные понятия о синтезе систем управления

Все математические задачи, решаемые в теории автоматического управления, можно объединить в два больших класса – задачи анализа и задачи синтеза систем автоматического управления.

В задачах анализа полностью известна структура системы, заданы, как правило, все параметры системы, и требуется оценить какое-либо ее статическое или динамическое свойство. К задачам анализа относятся расчет точности в установившихся режимах, определение устойчивости, оценка качества системы.

Задачи синтезаможно рассматривать как обратные задачам анализа: в них требуется определить структуру и параметры системы по заданным показателям качества. Простейшими задачами синтеза являются, например, задачи определения передаточного коэффициента разомкнутого контура по заданной ошибке или условию минимума интегральной оценки. Более сложные задачи синтеза будут рассмотрены в данной главе и далее.

Синтез системы автоматического управления – это процедура определения структуры и параметров системы по заданным показателям качества. Синтез является важнейшим этапом проектирования и конструирования системы. В общем случае при проектировании системы необходимо определить алгоритмическую и функциональную структуру, т. е. решить задачу полного синтеза.

Алгоритмическую структуру системы (или ее части) находят при помощи математических методов и на основании требований, записанных в четкой математической форме. Поэтому процедуру отыскания алгоритмической структуры часто называют теоретическим синтезом или аналитическим конструированием системы управления.

Синтез функциональной структуры – технический синтез системы заключается в выборе конкретных элементов (с учетом их физической природы) и согласовании статических и энергетических характеристик смежных элементов. Этот этап проектирования не имеет пока строгой математической основы и относится к области инженерного искусства. Выполняя синтез функциональной структуры, прежде всего, согласовывают входные и выходные сигналы смежных элементов. Сигналы должны иметь одинаковую физическую природу и одинаковые несущие величины. При выборе вида энергии и конструкции отдельных элементов руководствуются практическими соображениями об их простоте, надежности, минимальных габаритах и стоимости. Кроме этого учитывают условия эксплуатации элементов: температуру окружающей среды, агрессивность среды, вибрацию, взрывоопасность. На выбор функциональной структуры часто влияют традиции и опыт проектирования аналогичных систем.

Последовательность решения задачи полного синтеза может быть различной. В некоторых простых случаях задачу удается решить в идеальной последовательности: сначала определить при помощи математических методов алгоритмическую структуру системы, а затем – подобрать соответствующие конструктивные элементы. Однако применение этой последовательности при проектировании сколь-нибудь сложных промышленных систем управления, оказывается, по ряду причин невозможным. В первую очередь возникают трудности в подборе конструктивных элементов: в ограниченной номенклатуре серийно изготавливаемых средств управления может не оказаться устройств с необходимыми алгоритмическими свойствами. Поэтому задачу синтеза в большинстве случаев решают следующим образом.

Сначала, исходя из требований к назначению системы и учитывая условия ее работы, по каталогам серийного оборудования выбирают функционально необходимые элементы системы: регулирующий орган РО,исполнительное устройство ИУ,датчики Д.

Эти элементы вместе с объектом управления ОУ образуют неизменяемую часть системы.

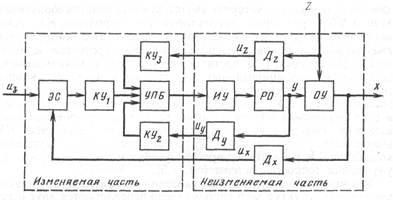
Затем на основании требований к статическим и динамическим свойствам системы определяют ее изменяемую часть, в которую входят усилительно-преобразующий блок УПБ и различные корректирующие устройства КУ. Алгоритмическую структуру изменяемой части находят с учетом свойств уже выбранных функционально необходимых элементов, а техническая реализация этой части осуществляется с использованием стандартных унифицированных регуляторов и различных корректирующих и компенсирующих устройств. Корректирующие устройства КУ₁ и КУ₂,включаемые в контур последовательно или в виде внутренней обратной связи, служат для улучшения динамических свойств системы. Компенсирующие устройства КУ₃ включаются между датчиком Д_f воспринимающим возмущающее воздействие, и усилительно-преобразующим блоком, и служат для улучшения точности системы.

Таким образом, процессы определения алгоритмической и функциональной структур всей системы тесно переплетаются друг с другом. Нередко их приходится выполнять по нескольку раз, чередуя между собой. Окончательное решение о структуре системы принимается, как правило, на основе компромисса между точностью и качеством, с одной стороны, и простотой и надежностью, с другой.

Заключительным этапом проектирования системы управления является параметрическая оптимизация – расчет настроечных параметров выбранного регулятора.

После решения задачи синтеза обычно выполняют анализ синтезированной системы: проверяют, обладает ли система необходимыми показателями точности, устойчивости и качества.

Моделирование систем на вычислительных машинах позволяет исследовать большое количество вариантов структур и параметров и тем самым существенно ускорить решение задачи синтеза.

Общие принципы синтеза алгоритмической структуры системы управления

1. Идеальная структура системы

Для решения задачи синтеза алгоритмической структуры должны быть известны передаточная функция W_о(p) объекта управления, возмущения у_в и х_в,действующие на входе и выходе объекта, а также помехи х_П,возникающие в каналах задания и измерения.

В простейшем случае, когда возмущающие воздействия на объект отсутствуют, управление можно осуществлять по разомкнутой схеме.

Если при этом передаточную функцию W_у(p) управляющего устройства принять равной

W_у(p)=1/W_о(p),

то обеспечится полная (структурная) компенсация инерционности объекта, и система управления будет практически мгновенно воспроизводить на выходе объекта задающее воздействие х_З.опт. Задание х_З.опт формируется специальным фильтром с передаточной функцией Ф_опт(р),которая выбирается так, чтобы фильтр как можно лучше пропускал все составляющие сигнала х_З и подавлял помеху х_П.

Если на объект действует возмущение х_в, которое поддается измерению, то теоретически можно синтезировать идеальную разомкнутую систему управления с полной компенсацией возмущения.

Причем, передаточная функция управляющего устройства W_у(p)=1/W_о(p), обеспечивающая полную компенсацию инерционности объекта, оказывается наилучшей и для компенсации («парирования») возмущения х_в.Действительно, при выполнении условия W_у(p)=1/W_о(p) всегда W_у(p)W_о(p)=1, поэтому полезная составляющая х_у на выходе объекта будет полностью уравновешивать возмущение х_в.

Но возмущение х_в, как правило, не удается измерить, и систему управления приходится строить по замкнутой схеме или принципу обратной связи. Для отыскания структуры идеальной замкнутой системы можно использовать идею косвенного измерения возмущения х_в с помощью модели объекта W_о.м(p).

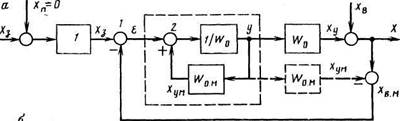
При W_о.м(p)=W_о(p), вычисляемый на выходе модели (штриховые стрелки) сигнал

х_в.м=х-х_ум=(х_у+х_в)-х_ум=х_в

является косвенно измеренным возмущением х_в и его можно, как и в предыдущей схеме, ввести в управляющее устройство с передаточной функцией 1/W_о(p) и, таким образом, снова получить идеальную разомкнутую структуру. В ней в соответствии с правилами структурных преобразований сигнал х_ум можно перенести на вход управляющего устройства и приложить к сумматору 2.Тогда управляющее устройство 1/W_о окажется охваченным внутренней положительной обратной связью, а сигнал после сумматора 1 будет соответствовать сигналу ошибки ε=х_З-х. Последнее означает, что система стала замкнутой и работает по принципу отрицательной обратной связи с регулятором (на рисунке штриховой прямоугольник)

W_р.и(p)=y(p)/ε(p)=(1/W_о(p))/(1-W_ом(p)W_о(p)).

При точном совпадении модели и объекта полученный регулятор будет работать как пропорциональный с k_Р=∞, что соответствует нулевым ошибкам по каналам задания и возмущения.

В общем случае, когда х_в≠0 и х_П≠0, алгоритмическая структура идеальной замкнутой системы сочетает в себе признаки обеих структур, обоснованных выше.

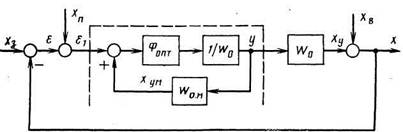
В этой идеальной структуре регулятор также содержит внутреннюю положительную обратную связь, звенья 1/W_о(p), W_ом(p), и кроме того, – оптимальный фильтр Ф_опт. Замкнутая система с таким регулятором теоретически эквивалентна идеальной разомкнутой системе управления по возмущению х_в, которая практически мгновенно воспроизводит задание х_З и полностью компенсирует возмущение х_в.Передаточная функция регулятора идеальной системы (на рисунке штриховой прямоугольник)

W_р.и(p)=y(p)/ε₁(p)=(Ф_опт(р)/1-Ф_опт(р))1/W_О(p).

Звено Ф_опт(р), входящее в прямую цепь регулятора, осуществляет оптимальную фильтрацию внешних воздействий и вырабатывает оптимальное задание х_Зопт. Обратная модель объекта 1/W_о(p) компенсирует его инерционность, а прямая W_ом(p) прогнозирует влияние управляющего воздействия u на управляемую величину х (вычисляет составляющую х_у на выходе объекта). Так как сигнал х_ум с выхода прогнозирующего звена поступает на вход регулятора с положительным знаком, то вся система после очередного изменения управляющего воздействия оказывается как бы разомкнутой. Вследствие этого реальная замкнутая система теоретически эквивалентна разомкнутой системе управления по возмущению х_В.

Используемое в идеальной системе включение последовательно с объектом звена в виде обратной модели объекта является принципиальной основой структурного и параметрического синтеза систем управления, а сам прием называется методом компенсации инерционности объекта.

В практических задачах синтеза чаще всего применяется частичная (параметрическая) компенсация – устранение влияния одной-двух (обычно самых больших) постоянных времени объекта.

Для этого последовательно с инерционным объектом

W_о(p)=k_о/(T_о1p+1)(T_о2p+1)…(T_оnp+1),

где T_о1>T_о2>…>T_оn,

включают форсирующее звено первого-второго порядка с передаточной функцией

W_к(p)=k_к(T_к1p+1)(T_к2p+1),

для которого постоянные времени должны быть равны компенсируемым постоянным времени объекта, т. е.

T_к1=T_о1; T_к2=T_о2,

и передаточный коэффициент k_к=1/k_о.

Практическая реализация систем с идеальной структурой и применение метода компенсации инерционности объекта связаны с определенными техническими ограничениями и препятствиями, которые не всегда могут быть преодолены. В частности:

- невозможно точно реализовать обратную передаточную функцию объекта W_у(p);

- форсирующие звенья вида W_к(p), используемые для частичной компенсации инерционности объекта, реально имеют свою инерционность;

- регулятор с внутренней положительной обратной связью обычно структурно неустойчив или имеет большой передаточный коэффициент, который вызывает нереализуемые управляющие воздействия.

Тем не менее, несмотря на невозможность практической реализации системы с идеальной структурой, она является теоретическим пределом, к которому необходимо стремиться при синтезировании высококачественных систем управления. В соответствии с идеальной структурой можно сформулировать фундаментальный принцип структурно-параметрической оптимизации систем управления с обратной связью

управляющее устройство должно содержать динамическое звено с передаточной функцией, равной или близкой обратной передаточной функции объекта.

2. Идеальный регулятор для объектов с запаздыванием

Определим структуру и передаточную функцию идеального регулятора для инерционных объектов с запаздыванием, которые можно описать следующей обобщенной передаточной функцией

W_о(p)=W’_о(p)e^-pτо,

где W’_о(p) – дробно-рациональная функция, характеризующая инерционную часть объекта; τ_о – чистое запаздывание объекта.

Учтем, что при подстановке передаточной функции W_о(p) в W_р.и(p) в передаточной функции регулятора появится сомножитель e^+pτо, который соответствует идеальному упредителю и точная реализация которого технически невозможна. Поэтому с целью упрощения искомой структуры регулятора и облегчения его технической реализации целесообразно допустить, чтобы для объектов, содержащих чистое запаздывание τ_о, идеальная система воспроизводила задающее воздействие с запаздыванием τ_о, т. е. чтобы

Ф_хЗ(р)=Ф_опт(p)=Ф^’_опт(p)e^-pτо,

где Ф^’_опт(p) – оптимальный фильтр для сигналов х₃ и х_П.

Тогда получим идеальный регулятор для объектов с запаздыванием

W_р.и(p)=(Ф^’_опт(p)/1-Ф^’_опт(p)e^-pτо)(1/W’_о(p)),

который называется регулятором Ресвика.

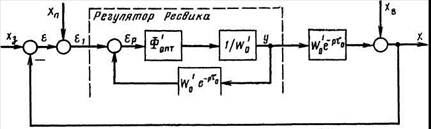
Внутренняя обратная связь регулятора Ресвика, содержащая звено чистого запаздывания, прогнозирует, какой сигнал должен появиться на выходе объекта после очередного изменения управляющего воздействия у. Так как эта связь положительная, то прогнозируемый сигнал постоянно компенсирует (нейтрализует) равный ему реальный выходной сигнал объекта. Результирующий сигнал ε_Р появляется только в первые моменты времени после изменения внешних воздействий х_З и х_П или х_в.Таким образом, благодаря дополнительной обратной связи, моделирующей динамику объекта, из основного контура как бы исключается чистое запаздывание τ_о, которое всегда ухудшает устойчивость системы и затрудняет решение задачи синтеза.

Как и в общем случае, практическая реализация идеальной системы управления объектом с запаздыванием связана с определенными техническими трудностями. Существенным недостатком системы с регулятором Ресвика является ее критичность или сильная чувствительность к малым вариациям запаздывания объекта: система устойчива только при точном равенстве запаздывания объекта τ_о и запаздывания τ_ом, моделируемого в объекте, т. е.

τ_о=τ_ом.

При несовпадении запаздываний система может стать неустойчивой. Можно показать, что в случае, когда Ф_опт(р)=k_опт для устойчивости замкнутой системы необходимо k_опт<0,5. При k_опт>0,5 малейшее нарушение равенства τ_о=τ_ом ведет к потере устойчивости, хотя при точном совпадении запаздываний коэффициент k_опт может быть сколь угодно большим.

Для повышения запаса устойчивости систем с регулятором Ресвика в их контур вводят дополнительные корректирующие звенья или ограничиваются неполной компенсацией инерционной части объекта. Естественно, что динамическая точность управления при этом ухудшается.

Идея нейтрализации запаздывания объекта реализуется также с помощью упредителя Смита,которым охватывают типовые регуляторы.

Нетрудно убедиться, что при большом передаточном коэффициенте (k_Р®∞) регулятор с упредителем Смита эквивалентен регулятору Ресвикас Ф_опт(р)=1.

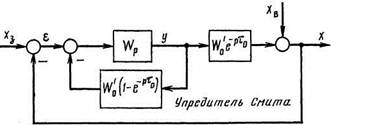
Систему с упредителем Смита технически реализовать легче, так как не требуется моделировать обратную передаточную функцию объекта.

Хотя регулятор Ресвика практически осуществить никогда не удается, анализ его свойств позволяет оценить предельные возможности управления объектами с запаздыванием.

Так, для наилучшего воспроизведения задающего воздействия g_З при отсутствии помехи (т. е. при Ф_опт(р)=1) регулятор Ресвика принимает вид

W_р.и(p)=[(1-e^-pτо)W’_о(p)]^-1,

а передаточные функции замкнутой системы по каналу х₃-х

Ф_хЗ(р)=e^-pτо

и по каналу х_в-х

Ф_хв(р)=1-e^-pτо.

Полученным функциям соответствуют идеальные переходные процессы прямоугольной формы, заканчивающиеся за минимально возможное время t_П=τ_о. По каналу у_в-х переходный процесс имеет плавный характер и длительность t_П≥(2-3) τ_о.

Наиболее трудно управляемыми являются объекты, содержащие только чистое запаздывание,

W_о(p)=k_оe^-pτо,

и для них лучше всего применять именно регулятор Ресвика или упредитель Смита, обеспечивающие структурную компенсацию запаздывания. Регулятор W_р.и(p) для объекта W_о(p) принимает вид

W_р.и(p)=y(p)/ε(p)=1/k_о(1-e^-pτо).

При медленных внешних воздействиях, для которых допустима приближенная замена

e^-pτо=1-pτ_о,

идеальный регулятор эквивалентен И-регулятору

W_р.и(p)≈k_и/p,

где k_и=1/k_оτ_о.

Отсюда можно сформулировать общее правило настройки регуляторов для объектов с запаздыванием

передаточный коэффициент регулятора должен быть обратно пропорционален передаточному коэффициенту объекта и времени запаздывания.

При высокочастотных воздействиях регулятор действует как дискретный: после каждого очередного изменения управляющего воздействия у «выжидает» в течение интервала τ_о и тем самым повышает устойчивость системы.

Дата добавления: 2014-11-15; просмотров: 1005; Нарушение авторских прав

Мы поможем в написании ваших работ!