
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
функции спроса и предложения
В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:
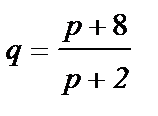 – спроса,
– спроса, 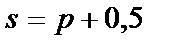 – предложения,
– предложения,
где p – цена товара.
Найти:
1) Равновесную цену p0.
2) Эластичность спроса и предложения для этой цены.
3) Изменение дохода при увеличении цены на 5% от равновесной.
Решение
1) Определяем равновесную цену p0, при которой спрос равен предложению.
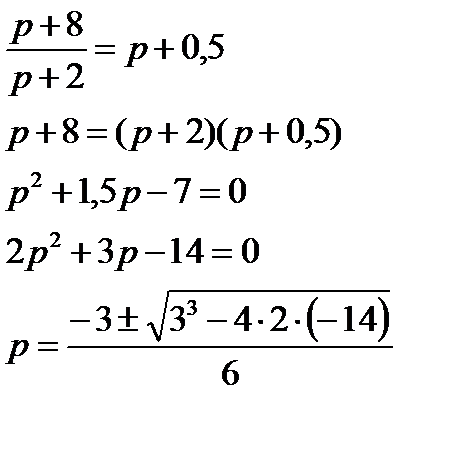
Отсюда p0=2. (Отрицательный корень отбрасываем, как не имеющий экономического смысла).
График зависимостей спроса и предложения от цены имеет вид:
2) Находим эластичности спроса и предложения для равновесной цены.
2.1. Находим производные q’(p) и s’(p).
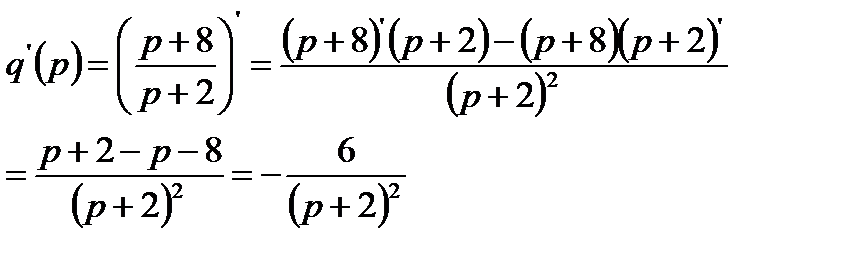
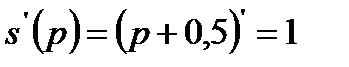
2.2. Получаем общие выражения для эластичностей спроса и предложения.
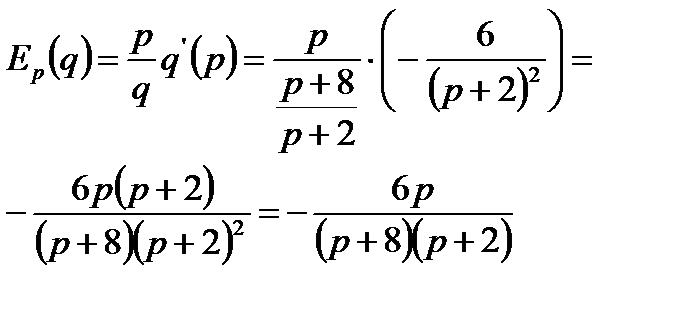
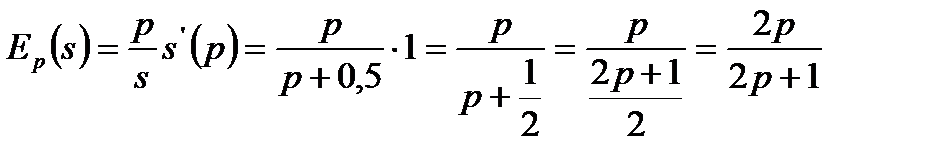
2.3. Вычисляем эластичности спроса и предложения при равновесной цене.
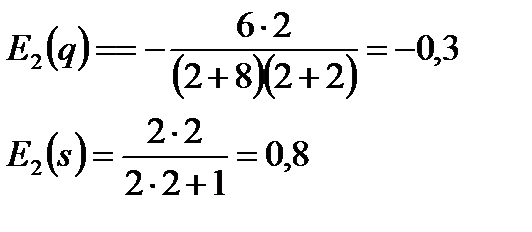
Таким образом, при увеличении цены на 1% от равновесного значения спрос уменьшается на 0, 3%, а предложение возрастает на 0,8%.
3) Выведем общее выражение для эластичности дохода R=pq по цене, пользуясь свойствами эластичности и подставим в него численные значения p0 и E2(s):
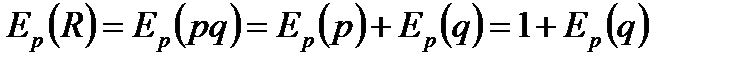
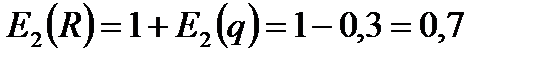
Это означает, что при увеличении цены на 1% от равновесного значения доход увеличивается на 0,7%. Следовательно, при увеличении цены на 5% от ее равновесного значения доход увеличится на 5×0,7%=3,5%.
Ответ:1) равновесная цена товара равна 2;
2) при увеличении цены на 1% от равновесного значения спрос уменьшается на 0, 3%, а предложение возрастает на 0,8%;
3) при увеличении цены на 5% от ее равновесного значения доход увеличится на 3,5%.
Пример 2.Даны результаты эмпирического исследования покупательского спроса 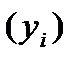 на какой-либо товар и изменение фактора
на какой-либо товар и изменение фактора 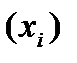 , влияющего на спрос.
, влияющего на спрос.
1. Построить экономико-математическую модель спроса на мебель местного производства в зависимости от денежных доходов населения на основе данных, полученных в результате спроса десяти групп семей (цифры условные):
| Денежные доходы населения в год, усл.ед. | 9,6 | 9,7 | 10,5 | 11,3 | 12,4 | 13,8 | 15,9 | 16,1 | 18,3 | 19,1 |
| Платежеспособный спрос населения на мебель в год, усл. ед. | 0,7 | 0,8 | 0,9 | 1,1 | 1,8 | 2,7 | 3,9 | 4,7 | 5,4 | 6,3 |
2. Провести логический и графический анализ исходных данных. Построить эмпирическую линию регрессии.
3. Рассчитать линейный коэффициент корреляции.
4. Провести подбор функции спроса и определить ее параметры, используя метод наименьших квадратов.
5. Построить теоретическую линию регрессии.
6. Рассчитать ошибку уравнения регрессии, теоретическое корреляционное отношение.
7. Осуществить прогноз по найденному уравнению регрессии для трех заданных значений
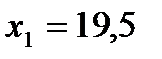 ,
, 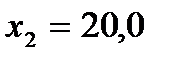 ,
, 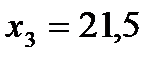 .
.
Решение. Первоначально проведем корреляционный анализ, позволяющий количественно оценить тесноту связи между признаком (платежеспособный спрос) и фактором (денежные доходы населения).
Наличие и количественную характеристику связи между признаком и фактором определим с помощью оценки коэффициента корреляции по формуле (2.35)
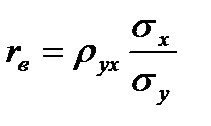 ,
,
где 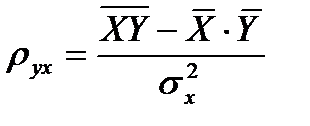 ,
, 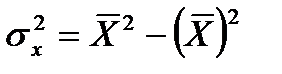 ,
, 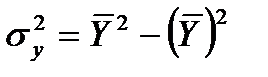 .
.
Исходные данные и промежуточные вычисления занесем в таблицу 2.1.
Таблица 2.1.
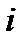
| 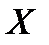
| 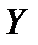
| 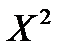
| 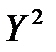
| 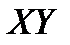
|
| 9,6 | 0,7 | 92,16 | 0,49 | 6,72 | |
| 9,7 | 0,8 | 94,09 | 0,64 | 7,76 | |
| 10,5 | 0,9 | 110,25 | 0,81 | 9,45 | |
| 11,3 | 1,1 | 127,69 | 1,21 | 12,43 | |
| 12,4 | 1,8 | 153,76 | 3,24 | 22,32 | |
| 13,8 | 2,7 | 190,44 | 7,29 | 37,26 | |
| 15,9 | 3,9 | 252,81 | 15,21 | 62,01 | |
| 16,1 | 4,7 | 259,21 | 22,09 | 75,67 | |
| 18,3 | 5,4 | 334,89 | 29,16 | 98,82 | |
| 19,1 | 6,3 | 364,81 | 39,69 | 120,33 | |
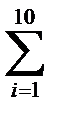
| 136,7 | 28,3 | 1980,11 | 119,83 | 452,77 |
Используя полученные суммы по столбцам, вычислим исходные статистические характеристики:
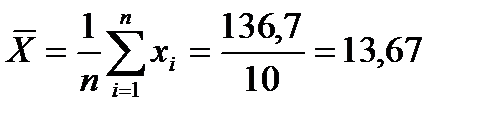 ,
, 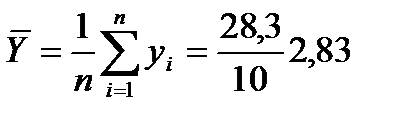 ,
, 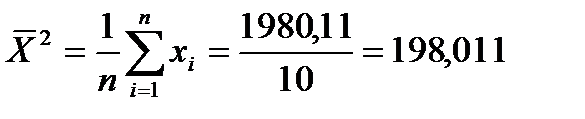 ,
, 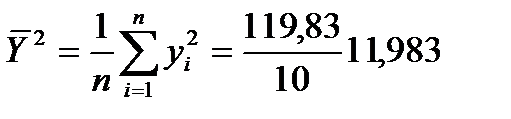 ,
, 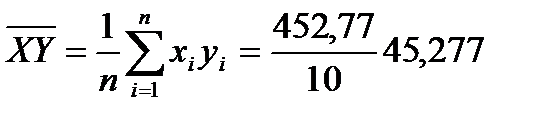 .
.
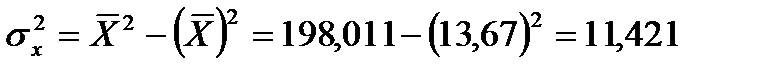 ,
, 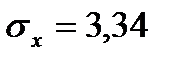 ,
,
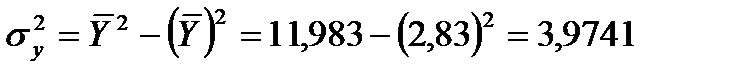 ,
, 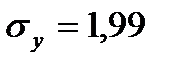 ,
,
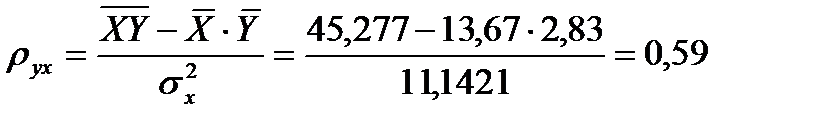 ,
, 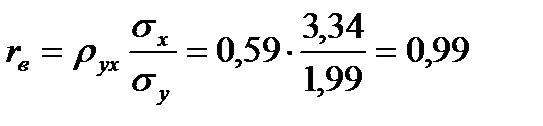 .
.
Выборочный коэффициент корреляции указывает на весьма высокую связь между денежными доходами населения и платежеспособным спросом на мебель. Этот факт подтверждается и таблицей Чеддока.
Регрессионный анализ проводится в три этапа:
- логический анализ;
- графический анализ;
- определения уравнения теоретической линии регрессии, т.е. установление функциональной зависимости между признаком и фактором.
При логическом анализе эмпирических данных спроса и значений влияющего на него фактора можно сделать предположение относительно наличия и направления связи между признаком и фактором. В нашем случае наблюдается связь между размером денежных доходов населения и спросом на мебель, причем с увеличением доходов населения спрос на мебель во всех опрошенных семьях повышается.
Графический анализ начинается с построения эмпирической линии регрессии. При этом по оси абсцисс откладывают значения фактора (в нашем примере – денежные доходы), а по оси ординат – значения признака (спрос). Точки на графике, соответствующие паре значений 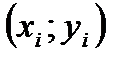 образуют поле корреляции. По характеру расположения точек на рис. 2.1. можно судить о направлении и форме связи. Соединив последовательно точки на графике, получим ломаную линию, являющуюся эмпирической линией регрессии. По ее виду можно предположить тип теоретической линии регрессии.
образуют поле корреляции. По характеру расположения точек на рис. 2.1. можно судить о направлении и форме связи. Соединив последовательно точки на графике, получим ломаную линию, являющуюся эмпирической линией регрессии. По ее виду можно предположить тип теоретической линии регрессии.
| y |
| x |
| M1 |
| M2 |
Экономико-математическая модель прогноза строится в виде уравнений регрессии, где в качестве зависимой переменной выступает признак (спрос), а в качестве независимых переменных – факторы. В нашей задаче признак (спрос) зависит только от одного фактора – денежных доходов населения. Следовательно, мы будем рассматривать однофакторную функцию. Уравнение регрессии при этом называют парной регрессией.
Теоретическая линия регрессии представляется либо прямой, либо кривой, описываемой некоторым математическим уравнением. В нашем случае, анализируя поле корреляции, можно предположить, что имеет место линейная зависимость. Поэтому будем искать уравнение теоретической линии регрессии в виде (2.28)
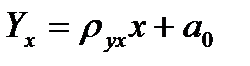
Рассчитаем параметры теоретического уравнения регрессии, используя метод наименьших квадратов. Система нормальных уравнений для случая линейной корреляционной зависимости, имеет вид (2.32)
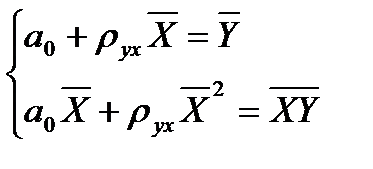
Подставляя найденные значения 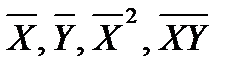 , получим систему уравнений в виде:
, получим систему уравнений в виде:
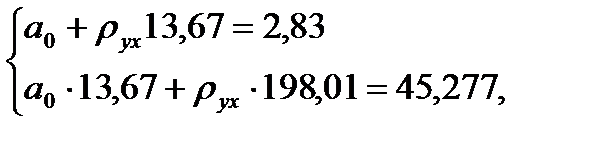
откуда 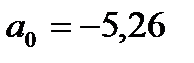 ,
, 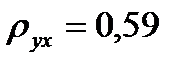
Итак, 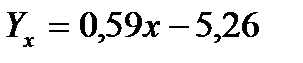 (2.37)
(2.37)
Параметр 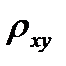 показывает среднее изменение признака при изменении фактора на единицу, т.е. с увеличением денежных доходов на 1 усл. ед., спрос на мебель возрастет на 0,59 усл. ед.
показывает среднее изменение признака при изменении фактора на единицу, т.е. с увеличением денежных доходов на 1 усл. ед., спрос на мебель возрастет на 0,59 усл. ед.
Для построения теоретической линии регрессии выберем два значения х, достаточно удаленных друг от друга, но лежащих в области изменения Х: например, 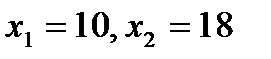 . Подставляя их поочередно в уравнение (2.37), получим:
. Подставляя их поочередно в уравнение (2.37), получим:
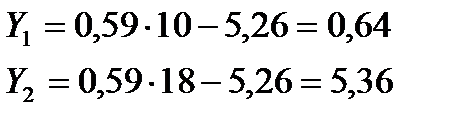
Наносим точки с координатами 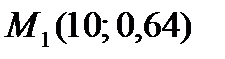 и
и 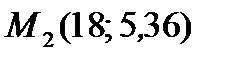 на рис. 2.1 и, соединив их, получим график прямой линии регрессии.
на рис. 2.1 и, соединив их, получим график прямой линии регрессии.
Далее необходимо оценить степень близости полученной экономико-математической модели к фактическим данным. Для этой цели можно использовать корреляционное отношение в виде: 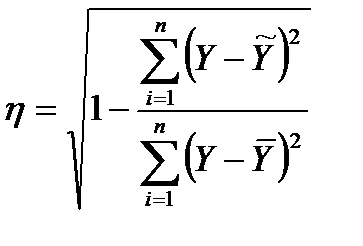 , где
, где 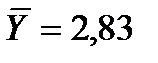 ,
, 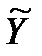 – выровненные значения, полученные по уравнению (2.37):
– выровненные значения, полученные по уравнению (2.37):
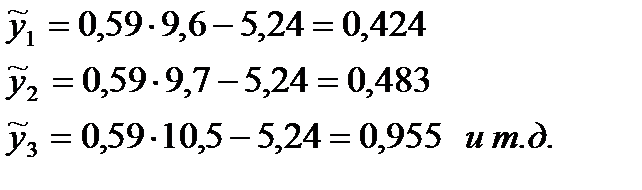
Для удобства расчета 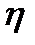 сведем необходимые данные в таблицу 2.2.
сведем необходимые данные в таблицу 2.2.
Таблица 2.2.
| i | Y | 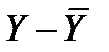
| 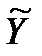
| 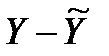
| 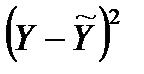
| 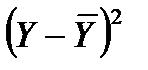
|
| 0,7 | -2,13 | 0,424 | 0,276 | 0,076 | 4,537 | |
| 0,8 | -2,03 | 0,483 | 0,317 | 0,100 | 4,121 | |
| 0,9 | -1,93 | 0,955 | -0,055 | 0,003 | 3,725 | |
| 1,1 | -1,73 | 1,427 | -0,327 | 0,107 | 2,993 | |
| 1,8 | -1,03 | 2,076 | -0,276 | 0,076 | 1,061 | |
| 2,7 | -0,13 | 2,902 | -0,202 | 0,041 | 0,017 | |
| 3,9 | 1,07 | 4,141 | -0,241 | 0,058 | 1,145 | |
| 4,7 | 1,87 | 4,259 | 0,441 | 0,194 | 3,497 | |
| 5,4 | 2,57 | 5,557 | -0,157 | 0,025 | 6,605 | |
| 6,3 | 3,47 | 6,029 | 0,271 | 0,073 | 12,041 | |
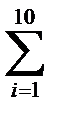
| 0,753 | 39,742 |
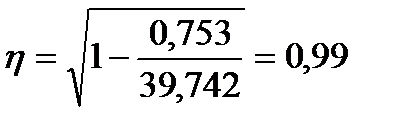 ;
; 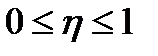
Ошибка уравнения регрессии, показывающая в среднем отклонения фактических данных от теоретических, равна
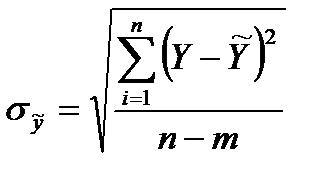
где 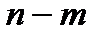 – число степеней свободы;
– число степеней свободы;
m – число определяемых в уравнении регрессии параметров

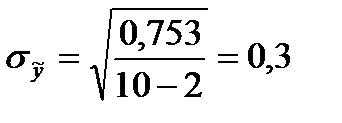
Проведенные расчеты показали значительную близость рассчитанной теоретической модели и фактической 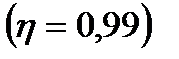 и незначительную ошибку параметров уравнения
и незначительную ошибку параметров уравнения 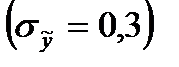 .
.
С помощью полученного уравнения регрессии можно осуществить прогноз показателя. Для этого в найденную функцию подставим задаваемые значения денежных доходов населения и получим планируемую величину платежеспособного спроса.
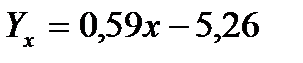
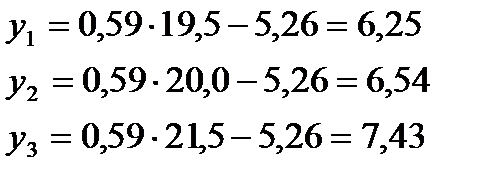
Практические задания
1. В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:
7) 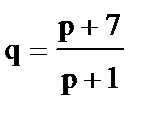 - спроса, - спроса,
| 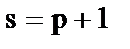 - предложения, - предложения,
|
9) 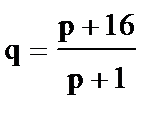 - спроса, - спроса,
| 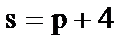 - предложения, - предложения,
|
где p – цена товара.
Найти:
1) Равновесную цену p0.
2) Эластичность спроса и предложения для этой цены.
3) Изменение дохода при увеличении цены на 5% от равновесной.
2. На основе приведенных в таблице данных необходимо:
1) Построить экономико-математическую модель спроса.
2) Провести логический и графический анализ исходных данных. Построить эмпирическую линию регрессии.
3) Рассчитать линейный коэффициент корреляции.
4) Провести подбор функции спроса и определить ее параметры, используя метод наименьших квадратов.
5) Построить теоретическую линию регрессии.
6) Рассчитать ошибку уравнения регрессии, теоретическое корреляционное отношение.
7) Осуществить прогноз по найденному уравнению регрессии для трех заданных значений xi.
| задание | № наблюдения | Прогноз | ||||||||||||||||||||||||
| x1 | x2 | x2 | ||||||||||||||||||||||||
| 7) | xi | 1,5 | 1,7 | 2,1 | 2,2 | 2,8 | 3,0 | 3,5 | 3,7 | 4,0 | 5,0 | 5,5 | 6,0 | 6,7 | ||||||||||||
| yi | 0,3 | 0,4 | 0,5 | 0,5 | 0,8 | 0,9 | 1,1 | 1,5 | 2,1 | 3,1 | ||||||||||||||||
| 9) | xi | 2,5 | 3,0 | 3,4 | 3,8 | 4,0 | 5,2 | 5,7 | 6,3 | 6,8 | 7,0 | 7,5 | 8,0 | 9,0 | ||||||||||||
| yi | 1,0 | 1,2 | 1,3 | 1,4 | 1,5 | 2,7 | 3,0 | 3,7 | 4,0 | 4,1 | ||||||||||||||||
| <== предыдущая страница | | | следующая страница ==> |
| Тема 9. Типы повышения эффективности менеджмента | | |
Дата добавления: 2014-11-20; просмотров: 576; Нарушение авторских прав

Мы поможем в написании ваших работ!