
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дифференцирование функций, заданных неявно
Пусть значения переменных х и у связаны уравнением F(x, y) = 0.
Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят, что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция.
Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным.
Для нахождения производной у'х неявной функции, нужно продифференцировать по х обе части равенства (1), учитывая, что у есть функция от х. Затем из полученного равенства выразить у'х.
Пример 1. Вычислить у'х.
у5+ху-х2 = 0
Продифференцируем обе части по х. Получим 5у4у'+у+ху'-2х=0. Выразим у'. y'(5у4+х) = 2х-у, у' =(2х-у)/(5у4+х).
Пример. Вычислить по определению производную функции 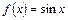 в произвольной точке
в произвольной точке  .
.
Решение. Берем 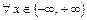 ,
, 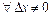 и рассматриваем
и рассматриваем 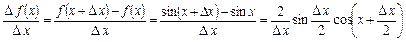 .
.
При 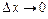
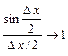 (по первому замечательному пределу
(по первому замечательному пределу 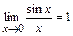 ), поэтому существует предел
), поэтому существует предел  . Здесь мы воспользуемся непрерывностью функции
. Здесь мы воспользуемся непрерывностью функции 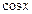 при всяком
при всяком 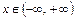 ,
, 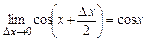 .
.
Пример.Найти 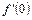 , если
, если 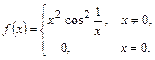
Решение. Берем 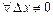 . Тогда соответствующее приращение функции в точке
. Тогда соответствующее приращение функции в точке 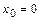 есть
есть
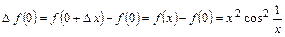 ,
, 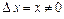 .
.
Поэтому 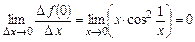 (по теореме о произведении ограниченной функции на бесконечно малую). Итак,
(по теореме о произведении ограниченной функции на бесконечно малую). Итак, 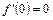 .
.
|
Пример. Написать уравнение касательной прямой к параболе 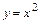 в точке
в точке 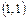 .
.
Решение. Поскольку 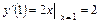 , то уравнение
, то уравнение 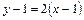 или
или 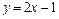 задаёт искомую касательную .
задаёт искомую касательную .
Итак, если для функции 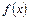 существует
существует 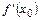 – конечное число, то существует единственная касательная (наклонная или горизонтальная прямая) к графику этой функции
– конечное число, то существует единственная касательная (наклонная или горизонтальная прямая) к графику этой функции 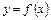 в точке
в точке 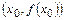 .
.
Обратное утверждение неверно, т.е. график функции может иметь в точке единственную касательную (вертикальную прямую), но при этом 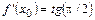 – не является конечным числом (не существует).
– не является конечным числом (не существует).
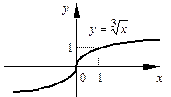
|
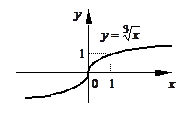 Пример. Для
Пример. Для 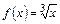 при
при 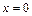 имеем
имеем 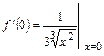 и
и 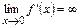 не существует, но касательная к
не существует, но касательная к 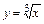 в точке
в точке 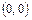 существует и совпадает с осью
существует и совпадает с осью 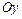 (касательная единственная!).
(касательная единственная!).
Если для функции 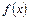 существует
существует 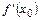 , то говорят, что
, то говорят, что 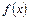 – дифференцируемаяв точке
– дифференцируемаяв точке 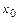 функция.
функция.
Функция 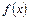 называется дифференцируемой на промежутке, если она дифференцируема в каждой точке этого промежутка.
называется дифференцируемой на промежутке, если она дифференцируема в каждой точке этого промежутка.
"Склеивание" частей графиков непрерывных функций часто приводит к появлению точек, в каждой из которых можно построить две касательные к графику (слева и справа от точки), т.е. производная функции в этих точках не существует (функция, не дифференцируемая в этих точках).
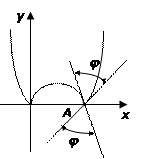 Пример. Для
Пример. Для 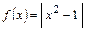 в каждой из точек
в каждой из точек  и
и 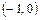 существует две касательные; их уравнения легко находятся: например, в точке
существует две касательные; их уравнения легко находятся: например, в точке 
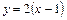 и
и 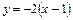 (дифференцируем функции
(дифференцируем функции 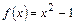 для
для 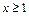 и
и 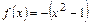 для
для 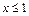 и вычисляем
и вычисляем 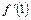 для каждого случая). Функция
для каждого случая). Функция 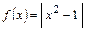 не имеет производных в точках
не имеет производных в точках 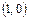 и
и 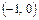 .
.
За угол 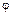 между кривыми принимается угол между касательными к кривым, проведенным в точке пересечения;
между кривыми принимается угол между касательными к кривым, проведенным в точке пересечения; 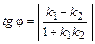 , здесь
, здесь  ,
, 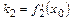 ,
,  – абсцисса точки пересечения.
– абсцисса точки пересечения.
В примере 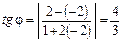 ,
,  .
.
Задача 3. Техника Дифференцирования – формальное вычисление производных функций по правилам и формулам.
Пусть для функций 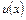 и
и 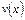 на
на 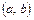 существуют производные функции,
существуют производные функции, 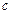 – произвольная постоянная; тогда на
– произвольная постоянная; тогда на 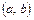 существуют производные суммы, произведения и частного этих функций (частное при условии
существуют производные суммы, произведения и частного этих функций (частное при условии 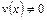 на
на 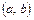 ), причем справедливы тождества:
), причем справедливы тождества:
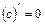 ;
; 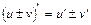 ;
; 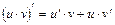 ;
;
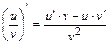 ;
; 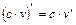 ;
;
 ;
; 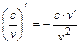 .
.
Если для функции 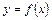 ,
, 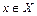 ,
,  существует
существует 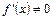 на
на 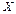 , то существует обратная функция
, то существует обратная функция 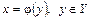 , производная которой существует и определяется по формуле
, производная которой существует и определяется по формуле
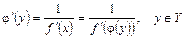 .
.
Если для функции 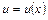 ,
, 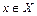 ,
, 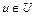 существует производная функция
существует производная функция 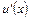 на
на 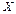 , а для функции
, а для функции 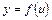 ,
, 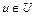 существует производная функция
существует производная функция 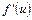 на
на 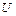 , то для сложной функции
, то для сложной функции 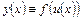 существует производная, причем
существует производная, причем
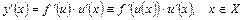 .
.
9. Лекционное занятие. Дифференцирование сложных функций и функций, заданных неявно и параметрически. 1
9.1 Функции, заданные параметрически, и их производные. 1
9.2 Дифференцирование функций, заданных неявно. 2
| <== предыдущая страница | | | следующая страница ==> |
| Функции, заданные параметрически, и их производные | | | ЭКОНОМИКА ПРЕДПРИЯТИЙ Князева Ирна Юрьевна (лекции) |
Дата добавления: 2014-11-24; просмотров: 420; Нарушение авторских прав

Мы поможем в написании ваших работ!