
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Функции, заданные параметрически, и их производные
Пусть зависимость между аргументом 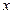 и функцией
и функцией 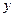 задана при помощи уравнений
задана при помощи уравнений  , где
, где 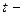 вспомогательная переменная, называемая параметром. Будем предполагать, что функция
вспомогательная переменная, называемая параметром. Будем предполагать, что функция 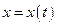 имеет обратную функцию
имеет обратную функцию  . Тогда равенства определяют сложную функцию
. Тогда равенства определяют сложную функцию 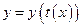 аргумента
аргумента 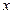 , заданную параметрическими уравнениями.
, заданную параметрическими уравнениями.
Теорема. Пусть функция 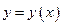 задана параметрическими уравнениями
задана параметрическими уравнениями 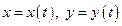 , где
, где 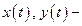 дифференцируемые функции, причем
дифференцируемые функции, причем 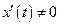 и функция
и функция 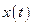 имеет обратную. Тогда функция
имеет обратную. Тогда функция 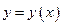 ─ дифференцируема, а ее производная находится по формуле:
─ дифференцируема, а ее производная находится по формуле: 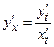 . Если при этом функции
. Если при этом функции 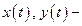 дважды дифференцируемы, то существует производная второго порядка
дважды дифференцируемы, то существует производная второго порядка 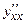 , причем
, причем 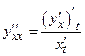 .
.
Доказательство. Как уже отмечалось, равенства (8.5) определяют сложную функцию 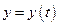 , где
, где  . По правилу дифференцирования сложной функции и обратной функции
. По правилу дифференцирования сложной функции и обратной функции 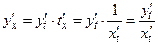 .
.
Аналогично 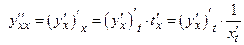 .
.
Пример. Найти 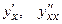 для функции
для функции 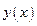 , заданной параметрическими уравнениями
, заданной параметрическими уравнениями 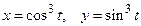 .
.
Решение. Используем полученные формулы:
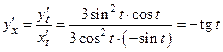 ,
, 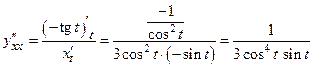 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Геометрия | | | Дифференцирование функций, заданных неявно |
Дата добавления: 2014-11-24; просмотров: 385; Нарушение авторских прав

Мы поможем в написании ваших работ!