
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основные элементарные функции, их графики
Функции и способы их задания
Понятие множества
План лекции
Множества и функции
Введение в анализ.
ЛЕКЦИИ 1-2
АНАЛИЗУ
Подготовила:
Платонова Татьяна Евгеньевна –
доцент кафедры высшей математики
Зеленодольск – 2014 г.
Множество – это совокупность некоторых объектов. Сами объекты называются элементами, или точками этого множества.
Множества обозначаются прописными буквами, а их элементы – строчными. а означает, что а есть элемент множества
означает, что а есть элемент множества 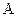 . b
. b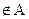 – b не является элементом множества (или b
– b не является элементом множества (или b 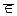
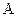 ).
).
Пустое множество не содержит ни одного элемента и обозначается Æ. Например, множество действительных корней уравнения 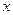 2 +1 = 0 пусто.
2 +1 = 0 пусто.
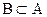 - множество
- множество  состоит из элементов множества
состоит из элементов множества 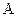 , т.е.
, т.е.  является подмножеством
является подмножеством 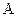 .
.
Равные множества состоят из одних и тех же элементов.
Действия над множествами:
- объединение множеств 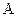 и
и : С =
: С = 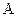
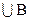 – множество С состоит из элементов, принадлежащих хотя бы одному из множеств – А или В; С называется объединением А и В;
– множество С состоит из элементов, принадлежащих хотя бы одному из множеств – А или В; С называется объединением А и В;
- пересечение двух множеств А и В: D = 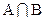 – множество D состоит из элементов, которые принадлежат одновременно А и В; D называется пересечением А и В;
– множество D состоит из элементов, которые принадлежат одновременно А и В; D называется пересечением А и В;
- разностьмножеств А и В: Е = А\В – множество Е состоит из всех элементов А, не принадлежащих множеству В;
Пример. Даны числовые множества А = {1,3,6,8}, B = {2,4,6,8}. Найти их объединение, пересечение и разность.
Решение.  = {1,2,3,4,6,8};
= {1,2,3,4,6,8}; 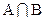 = {6,8}; А\В = {1,3}.
= {6,8}; А\В = {1,3}.
- дополнение множества 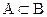 – это множество Ас, состоящее из всех элементов множества В, не принадлежащих А.
– это множество Ас, состоящее из всех элементов множества В, не принадлежащих А.
Множества, элементами которых являются действительные числа, называются числовыми. Известны следующие числовые множества: R – действительных чисел; Q – рациональных чисел; I – иррациональных чисел; Z – целых чисел; N – натуральных чисел. Очевидно, что
N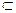 Z
Z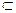 Q
Q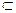 R, I
R, I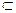 R, R = Q
R, R = Q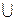 I.
I.
Геометрически множество R изображается точками числовой прямой (числовой оси). Между множеством действительных чисел и точками числовой прямой существует взаимно однозначное соответствие, т.е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой соответствует действительное число.
Множество Х, элементы которого удовлетворяют неравенству  , называется отрезком (сегментом) [a; b]; если неравенству а<x<b, то интервалом (a; b). Неравенства a
, называется отрезком (сегментом) [a; b]; если неравенству а<x<b, то интервалом (a; b). Неравенства a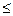 x<b и a<x
x<b и a<x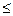 b называются полуинтервалами соответственно [a; b) и (а; b]. Существуют также бесконечные интервалы и полуинтервалы: (-
b называются полуинтервалами соответственно [a; b) и (а; b]. Существуют также бесконечные интервалы и полуинтервалы: (- ; а), (b;
; а), (b;  ), (-
), (- ; a], [b;
; a], [b;  ).Их также называют промежутками Х.
).Их также называют промежутками Х.
Абсолютная величина разности двух чисел | х – а | означает расстояние между точками х и а числовой прямой как для случая x<a, так и для случая х>a.
| х – а |
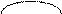 х < а
х < а
 x· a· x
x· a· x
| х – а |
х > а

 · · x
· · x
а х
Поэтому решениями неравенства |х–а|< , где
, где  >0, будут точки интервала (а –
>0, будут точки интервала (а – , а +
, а + ). Этот интервал называется
). Этот интервал называется  –окрестностью точки а.
–окрестностью точки а.
 |
 · e · e · х
· e · e · х
а – a а +
a а +
| <== предыдущая страница | | | следующая страница ==> |
| ПО МАТЕМАТИЧЕСКОМУ | | | Понятие функции |
Дата добавления: 2014-02-28; просмотров: 514; Нарушение авторских прав

Мы поможем в написании ваших работ!