Понятие функции

Постоянная величина – это величина, сохраняющая одно и то же значение. Если величина сохраняет постоянное значение лишь в условиях данного процесса, то она называется параметром.

Переменная – это величина, которая может принимать различные числовые значения.

Если каждому элементу х ÎХ ставится в соответствие вполне определенный элемент y Î Y, то говорят, что на множестве Х задана функция y = f(x).

При этом х называется независимой переменной или аргументом, y – зависимойпеременной, а буква f обозначает закон соответствия.

Множество Х называется областьюопределения (существования) функции, а множество Y – областьюзначений функции.

Способы заданий функций:

1. Аналитический способ. В этом случае функция задается формулой вида y = f(x).

2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции f(x).

3. Графическийспособ состоит в изображении графика функции – множества точек плоскости (x, y), абсциссы которых есть значения аргументов х, а ординаты – соответствующие им значения функции y = f(x).

4. Словесный способ, если функция описывается правилом ее составления.

Основные свойства функций:

1. Четность и нечетность. Функция y = f(x) называется четной, если для любых значений х из области определения f(–x) = f(x), и нечетной, если f(–x) = –f(x). В противном случае функция f(x) называется функцией общего вида.

Пример: функция y = x² – четная, y = x³ – нечетная, y = x²+ x³ – общего вида.

График четной функции симметричен относительно оси ординат, а нечетной функции – относительно начала координат.

2. Монотонность. Функция f(x) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

(х₁,х₂ Î Х, х₂>x₁, f(x₂)>f(x₁) – функция возрастающая, f(x₂)<f(x₁) – функция убывающая). Возрастающие и убывающие функции называются монотонными.

y y

y = f(x) y = f(x)

x x

возрастающая убывающая

функция функция

3. Ограниченность. Функция y = f(x) называется ограниченной на промежутке Х, если существует 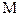> 0 (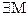> 0) такое, что | f (x)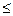 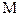|, x ÎX ( т.е. для любого х Î Х).

4. Периодичность. Функция y = f(x) называется периодической с периодом T ≠ 0, если для любого х Î Х f(x+T) = f(x) (x ÎX f(x+T) = f(x)).

Дата добавления: 2014-02-28; просмотров: 536; Нарушение авторских прав

Мы поможем в написании ваших работ!