Элементарные функции

Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.

Функция называется неявной, если она задана уравнением F (x, y) = 0, не разрешенным относительно зависимой переменной.

Пусть y = f(x) есть функция от независимой переменной х, определенной на промежутке Х с областью значений Y. Поставим в соответствие каждому yÎY единственное значение хÎХ, при котором f(x) = y. Тогда полученная функция х = j(x), определенная на промежутке Y с областью значений Х, называется обратной. Поскольку обычно независимую переменную обозначают х, а функцию через y, то обратная функция примет вид 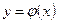, а также y = f^--1(x), Например, для функции y = a^x обратной будет функция х = log_ay или в обычных обозначениях y = log_ax.

Можно доказать, что для любой строго монотонной функции y = f(x) существует обратная функция. Графики взаимно обратных функций симметричны относительно биссектрисы 1-го и 3-го координатных углов.

y

y = a^x

₁_

y = log_ax

^|₁x

Пусть функция y = f(u) есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u, в свою очередь, является функцией u = j(x) от переменной х, определенной на множестве Х с областью значений U. Тогда y = f [j (x)] называется сложной функцией (композицией функций, суперпозицией функций, функциейот функции).

Например, y = lg sin x – сложная функция, т.к. ее можно представить в виде y = lg(u), где u = sin x.

Основные элементарные функции – это следующие функции:

1. Степенная функция: y = xⁿ; y = x^-n; y = .

2. Показательная функция: y = a^x.

3. Логарифмическая функция: y = log_ax.

4. Тригонометрические функции: y = sin x; y = cos x; y = tg x; y = ctg x.

5. Обратные тригонометрические функции: y = arcsin x; y = arccos x; y = arctg x; y = arcctg x.

Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.

Например, функция:

y =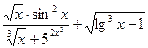

является элементарной, т.к. здесь число операций сложения, вычитания, умножения, деления и образования сложной функции (sin²x,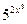, lg³x,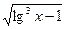) конечно.

Неэлементарными являются, например, функции y = | x | и y = [x], где [x] – целая часть х.

y y

₃_

y = | x | y = [x]

₂_

₁_

x ₀^|₁ ^|₂ ^|₃ ^|₄x

 

Элементарные функции делятся на алгебраическиеи трансцендентные.

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:

- целаярациональнаяфункция (многочленили полином):

y = a₀xⁿ + a₁x^n-1 +…+ a_n-1x + a_n;

- дробно-рациональная функция – отношения двух полиномов;

- иррациональная функция, если в составе операций над аргументом имеется извлечение корня.

Всякая неалгебраическая функция называется трансцендентной. Это показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.

Пусть задан график функции y = f(x). Тогда справедливы следующие утверждения:

1. График функции y = f(x+a) есть график y = f(x), сдвинутый на |а| единиц параллельно оси Оy (вдоль оси Oх); при a > 0 – влево, при a < 0 – вправо.

2. График функции y = f(x)+b есть график y = f(x), сдвинутый |b| единиц параллельно оси Оx (вдоль оси Oy); при b > 0 – вверх, при b< 0 – вниз.

3. График функции y = mf(x) (m≠0) есть график y = f(x), растянутый при m > 1 в m раз или сжатый при 0 < m <1 в m раз вдоль оси Oy. При m < 0 график функции y = mf(x) есть зеркальное отображение графика y = -mf(x) от оси Ox.

4. График функции y = f(kx) (k≠0) есть график y = f(x), сжатый при k > 1 в k раз или растянутый при 0 < k < 1 в k раз вдоль оси Ox. При k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(-kx) от оси Oy.

 

Вопросы для контроля:

---

<== предыдущая страница	|	следующая страница ==>
Понятие функции	|	Предел числовой последовательности

---

Дата добавления: 2014-02-28; просмотров: 657; Нарушение авторских прав

---

Поделиться с ДРУЗЬЯМИ:

Мы поможем в написании ваших работ!