Предел числовой последовательности

Предел функции

Предел числовой последовательности

Пределы и непрерывность.

Лекции 2-3

Постройте график и расскажите о свойствах функций

Приведите примеры числовых и нечисловых множеств

2. Что такое функция? Как можно задать функцию

План лекции:

Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число a_n, то говорят, что задана числовая последовательность {a_n}:

a₁, a₂,…,a_n… .

Другими словами, числовая последовательность – это функция натурального аргумента a_n = f(n).

Числа a₁, a₂,…,a_n называются членами последовательности, а число a_n – общим или n-м членом данной последовательности.

Примеры: 2, 4, 6, …2n, … (монотонная неограниченная); 1, 0, 1, 0, … (немонотонная ограниченная).

Число А называется пределом числовой последовательности {a_n}, если для любого сколь угодно малого e > 0 найдется такой номер N(e), зависящий от e, что для всех членов данной последовательности с номерами n > N(e) верно неравенство

|a_n - A| < e (1)

Предел числовой последовательности обозначается lim a_n = A или a_n ® ¥ при n ® ¥. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Используются следующие логические символы (кванторы): " (любой), $ (существует), Û (равносильность или эквивалентность). Тогда определение предела можно записать в виде:

(A = 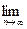a_n) Û ("e > 0 $ N(e) : "n > N(e) | a_n – A | < e)

Смысл определения: для достаточно больших n члены последовательности {a_n} сколь угодно мало отличаются от числа А, по абсолютной величине меньше, чем на e, каким бы малым оно ни было.

Дата добавления: 2014-02-28; просмотров: 868; Нарушение авторских прав

Мы поможем в написании ваших работ!