Предел функции

Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности, если для любого e > 0 найдется такое S > 0, что для всех |х| > S верно неравенство

| f(x) – A | < e (2)

Предел функции обозначаетсяf(x) = A, или f(x) ® A при х ® ¥.

(A = 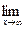f(x) Û ("e > 0 $ S = S(e) > 0 : "x : | x | > S | f(x) – A | < e)

Это предел функции в бесконечности.

Число А называется пределом функции f(x) при х ® х₀, если для "e > 0 $ d = d(e) > 0 : "x ¹ x_0, |х – x₀| < d выполняется неравенство | f(x) – A | < e.

Смысл определения: для всех значений х, достаточно близких к х₀, значения f(x) как угодно мало отличаются от числа А.

Замечание 1. Определение предела не требует существования функции в самой точке х₀, поскольку предполагается, что х стремится к х₀, но не достигает значения х₀. Поэтому наличие или отсутствие предела при х ® х₀ определяется поведением функции в окрестности точки х₀, но не связано с существованием функции в самой точке х₀.

Замечание 2. Если при х ® х₀ х принимает только значения, меньшие х₀, и при этом функция f(x) стремится к некоторому числу А, то говорят об одностороннем пределе функции слева:

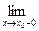f(x) = A

Аналогично, если при х ® х₀ х > х₀, то говорят об одностороннем пределе функции справа, т.е:

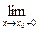f(x) = A

При этом, если 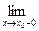f(x) = 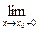f(x), то 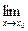f(x) = A.

Дата добавления: 2014-02-28; просмотров: 519; Нарушение авторских прав

Мы поможем в написании ваших работ!