
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Геометрия
|
Читайте также: |
Задание 4g.
Прямоугольник. Гл.V, §1. п.39-41, §2. п.45.
Сдать до 15.11.2014
1.В прямоугольнике АВСD О - точка пересечения диагоналей АС и ВD, < АОD = 60°, меньшая сторона ВС = 8см. Найдите: 1) < ОСD; 2) диагональ ВD.
2. В окружности с центром в точке О проведены диаметры АС и ВD. 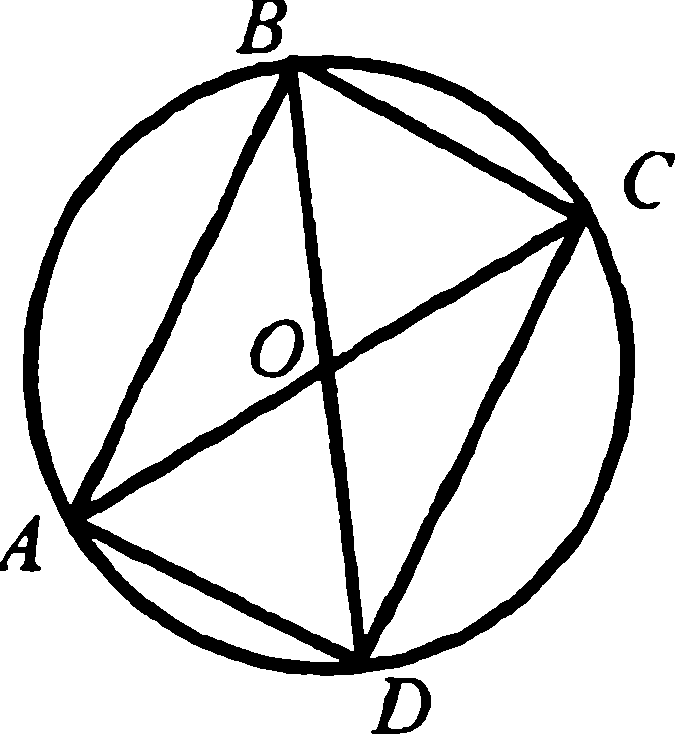 Докажите, что четырёхугольник АВСD – прямоугольник.
3. Периметр прямоугольника АВСD равен 30см. Биссектрисы углов А и D пересекаются в точке М, принадлежащей стороне ВС. Найдите стороны прямоугольника.
4. Перпендикуляры опущенные из точки пересечения диагоналей прямоугольника на две его соседние стороны равны 5см и 7см. Найдите периметр прямоугольника.
5. Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны на 5см меньше, чем до меньшей стороны. Найдите стороны прямоугольника, если его периметр равен 44см.
6. Докажите, что в прямоугольном треугольнике медиана, проведённая из вершины прямого угла равна половине гипотенузы.
7*. В треугольнике АВС известно, что <С = 90°, АС = ВС = 6см. Прямоугольник СМКN построен так, что точка М принадлежит катету АС, точка N – катету ВС, а точка К – гипотенузе АВ. Найдите РСМКN. Докажите, что четырёхугольник АВСD – прямоугольник.
3. Периметр прямоугольника АВСD равен 30см. Биссектрисы углов А и D пересекаются в точке М, принадлежащей стороне ВС. Найдите стороны прямоугольника.
4. Перпендикуляры опущенные из точки пересечения диагоналей прямоугольника на две его соседние стороны равны 5см и 7см. Найдите периметр прямоугольника.
5. Расстояние от точки пересечения диагоналей прямоугольника до его большей стороны на 5см меньше, чем до меньшей стороны. Найдите стороны прямоугольника, если его периметр равен 44см.
6. Докажите, что в прямоугольном треугольнике медиана, проведённая из вершины прямого угла равна половине гипотенузы.
7*. В треугольнике АВС известно, что <С = 90°, АС = ВС = 6см. Прямоугольник СМКN построен так, что точка М принадлежит катету АС, точка N – катету ВС, а точка К – гипотенузе АВ. Найдите РСМКN.
| Задание 6(g). Квадрат. Гл.V, §3. п.46. Сдать до 28.11.2014 1. Докажите, что прямоугольник, диагонали которого перпендикулярны, является квадратом 2. На стороне ВС квадрата АВСD отметили точку К так, что АК = 2ВК. Найдите <КАD. 3. Диагональ квадрата равна 4см. Его сторона является диагональю второго квадрата. Найдите сторону второго квадрата. 4. В прямоугольнике АВСD биссектрисы углов А и В пересекают стороны ВС и АD в точках Е и К соответственно. Докажите, что четырёхугольник АВЕК – квадрат. 5. Постройте квадрат по его периметру. 6*. Вершины М и К равностороннего треугольника АМК принадлежат сторонам ВС и СD квадрата АВСD. Докажите что МК ǁ ВD. | |
Задание 7(g).
Средняя линия треугольника. Гл.VII, §3. п.62. Сдать до 6.12.2014
1. Стороны треугольника равны 6см, 8см и 12см. Найдите средние линии этого треугольника.
2. Докажите, что периметр треугольника, стороны которого являются средними линиями треугольника АВС, равен половине периметра АВС.
3. Докажите, что средние линии треугольника разбивают его на четыре равных треугольника.
4. Докажите, что высота АМ ΔАВС перпендикулярна его средней линии, соединяющей середины сторон АВ и АС.
5. Средняя линия равнобедренного треугольника, параллельная основанию равна 6см. Найдите стороны
данного треугольника, если его периметр равен 46.
6. Докажите, что середины сторон четырёхугольника 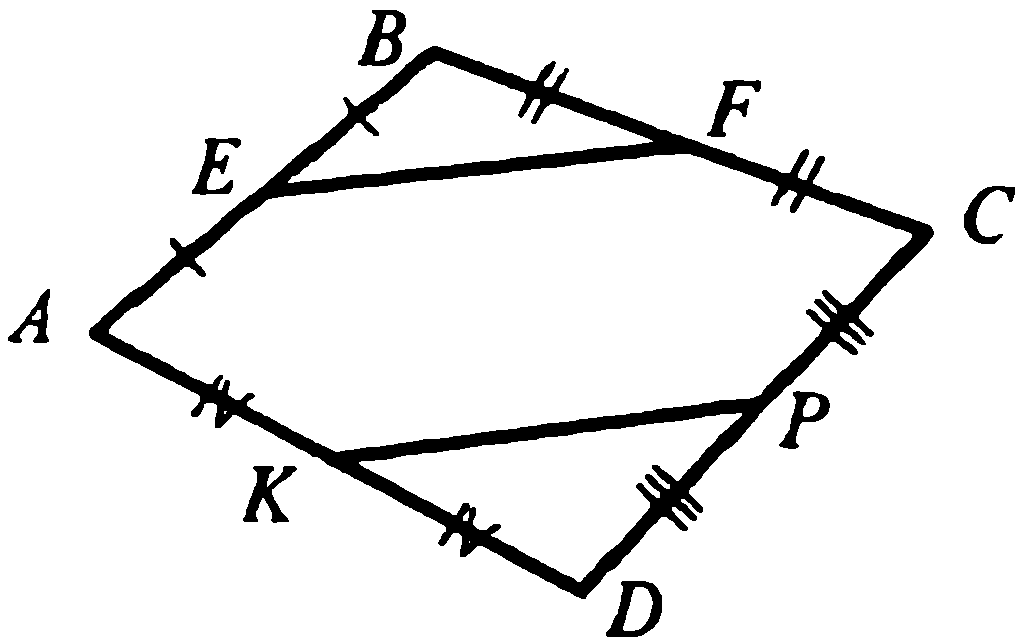 являются вершинами параллелограмма.
7*. Через вершины ΔАВС проведены прямые, параллельные его сторонам. Эти прямые пересекаются в точках А1, В1, С1. Докажите, что точки А , В, С делят Стороны Δ А1В1С1 пополам. являются вершинами параллелограмма.
7*. Через вершины ΔАВС проведены прямые, параллельные его сторонам. Эти прямые пересекаются в точках А1, В1, С1. Докажите, что точки А , В, С делят Стороны Δ А1В1С1 пополам.
| ||
Задание 5(g).
Ромб. Гл.V, §3. п.46. Сдать до 22.11.2014
1. Докажите, что если две соседние стороны параллелограмма равны, то он является ромбом.
2. В ромбе АВСD известно, что <С = 140°, а диагонали пересекаются в точке О. Найдите углы ΔАОВ.
3. Найдите периметр ромба АВСD,<А=60°, ВD=9см.
4. Найдите углы ромба, если его сторона образует с
диагоналями углы, которые относятся как 2 : 7.
5. Отрезки ВF и DЕ – высоты ромба АВСD. 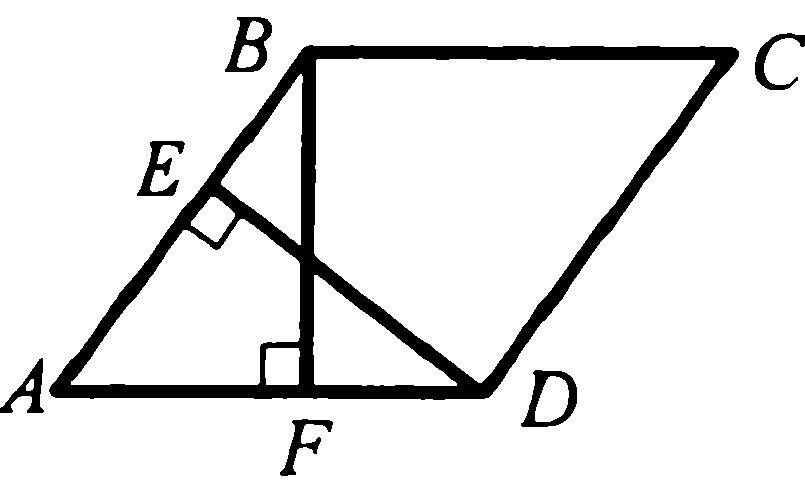 Докажите, что BF = DE.
6. В ромбе АВСD точки Е и F – середины сторон ВС и СD. Докажите, что <АЕ = <АF.
7. Угол между высотой и диагональю ромба, проведенными из одной вершины, равен 42°. Найдите углы ромба.
8*. На сторонах АВ и АD ромба АВСD отложены равные отрезки АE и АF. Докажите, что <СЕF=<CFE. Докажите, что BF = DE.
6. В ромбе АВСD точки Е и F – середины сторон ВС и СD. Докажите, что <АЕ = <АF.
7. Угол между высотой и диагональю ромба, проведенными из одной вершины, равен 42°. Найдите углы ромба.
8*. На сторонах АВ и АD ромба АВСD отложены равные отрезки АE и АF. Докажите, что <СЕF=<CFE.
|
Задание 7(g)
Трапеция. Средняя линия трапеции. Гл.V, §2. п.44. Сдать до 13.12.2014
1. Периметр трапеции равен 49см, боковые стороны – 5,6см и 7,8см. Найдите основание трапеции, если одно из них на 7,7см больше другого.
2. Найдите углы трапеции АВСD, прилежащие к боковой стороне СD, если <С :< D = 8 : 7.
3. В равнобедренной трапеции угол между боковой стороной и высотой, поведенной из вершины тупого угла, равен 23°. Найдите углы трапеции.
4. Один из углов равнобедренной трапеции равен 60°, боковая сторона равна 18см, а сумма оснований – 50см. Найдите основания трапеции.
5. Диагональ равнобедренной трапеции образует с основанием угол 32°, а ее боковая сторона равна меньшему основанию. Найдите углы трапеции.
6. Диагонали трапеции АВСD 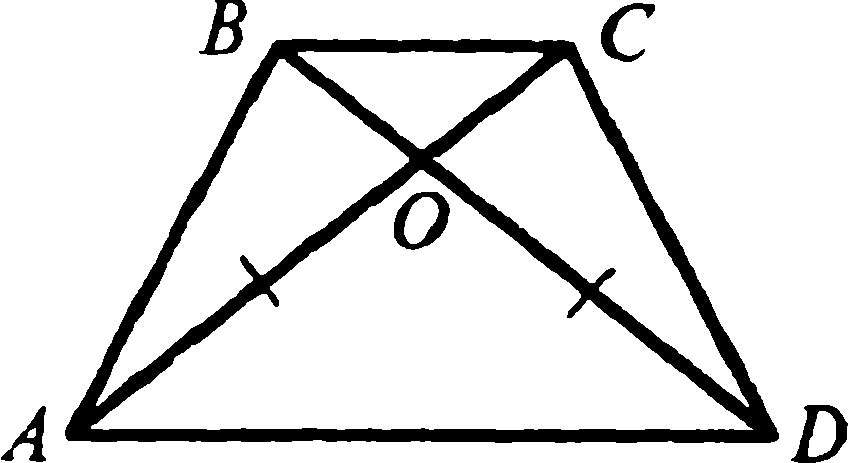 пересекаются в точке О. Отрезки ОА и ОD равны. Докажите, что АВ = СВ.
7. Средняя линия трапеции равна 8см, а одно из оснований – 5см. Найдите второе основание трапеции.
8. Через вершину С трапеции АВСD проведена прямая, которая параллельна боковой стороне АB и пересекает большее основание АD в точке Е. ВС = 8см, ЕС = 5см. Найдите среднюю линию трапеции АВСD.
9. Средняя линия трапеции в 2 раза больше меньшего основания и на 8см меньше большего основания. Найдите основания трапеции
10* .Средняя линия прямоугольной трапеции равна 12 см, а высота, проведенная из вершины тупого угла трапеции, делит ее основание на отрезки, длины которых относятся как 3:2, считая от вершины прямого угла. Найдите основание трапеции.
11*. Диагональ равнобедренной трапеции равна 14см и образует с основанием угол 60°. Найдите среднюю линию трапеции.
12*. Докажите, что если высота равнобедренной трапеции равна ее средней линии, то диагонали трапеции перпендикулярны.
__________________________________________________
Диагностическая контрольная работа № 2
1. Диагонали прямоугольника АВСD пересекаются в точкен О. Найдите угол между диагоналями, если <АВО = 30°.
2. Диагонали ромба пересекаются в точке О. Найдите углы ΔКОМ, если <МNP =80°.
3. Найдите периметр ромба АВСD, если <В = 120°.
4. В прямоугольной трапеции АВСD пересекаются в точке О. Отрезки ОА и ОD равны. Докажите, что АВ = СВ.
7. Средняя линия трапеции равна 8см, а одно из оснований – 5см. Найдите второе основание трапеции.
8. Через вершину С трапеции АВСD проведена прямая, которая параллельна боковой стороне АB и пересекает большее основание АD в точке Е. ВС = 8см, ЕС = 5см. Найдите среднюю линию трапеции АВСD.
9. Средняя линия трапеции в 2 раза больше меньшего основания и на 8см меньше большего основания. Найдите основания трапеции
10* .Средняя линия прямоугольной трапеции равна 12 см, а высота, проведенная из вершины тупого угла трапеции, делит ее основание на отрезки, длины которых относятся как 3:2, считая от вершины прямого угла. Найдите основание трапеции.
11*. Диагональ равнобедренной трапеции равна 14см и образует с основанием угол 60°. Найдите среднюю линию трапеции.
12*. Докажите, что если высота равнобедренной трапеции равна ее средней линии, то диагонали трапеции перпендикулярны.
__________________________________________________
Диагностическая контрольная работа № 2
1. Диагонали прямоугольника АВСD пересекаются в точкен О. Найдите угол между диагоналями, если <АВО = 30°.
2. Диагонали ромба пересекаются в точке О. Найдите углы ΔКОМ, если <МNP =80°.
3. Найдите периметр ромба АВСD, если <В = 120°.
4. В прямоугольной трапеции АВСD 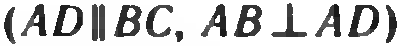 диагональ АС перпендикулярна к боковой стороне СD, <D = 30°. Найдите меньшее основание трапеции, если большее основание равно 24см. диагональ АС перпендикулярна к боковой стороне СD, <D = 30°. Найдите меньшее основание трапеции, если большее основание равно 24см.
| Задание 8(g)
Площадь прямоугольника и квадрата. Гл.VI, §1. п.50. Сдать до 20.12.2014
1.Найдите площадь прямоугольника ABCD, 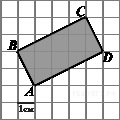 считая стороны квадратных клеток равными 1.
2. Площадь прямоугольника равна 270см2, а его стороны относятся как 5:6. Чему равны стороны прямоугольника?
3. Найдите площадь прямоугольника считая стороны квадратных клеток равными 1.
2. Площадь прямоугольника равна 270см2, а его стороны относятся как 5:6. Чему равны стороны прямоугольника?
3. Найдите площадь прямоугольника  , если его периметр равен 18, и одна сторона на 3 больше другой.
4. Найдите диагональ квадрата , если его периметр равен 18, и одна сторона на 3 больше другой.
4. Найдите диагональ квадрата 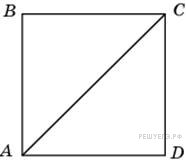 , если его площадь равна 2.
5. Как изменится площадь и периметр квадрата, если его диагональ увеличить в 4 раза?
6. Постройте квадрат, площадь которого равна сумме площадей двух данных квадратов.
7. Найдите периметр квадрата равновеликого (имеющего равную площадь) прямоугольнику со сторонами 2см и 32см.
8. Расход эмалевой краски на однослойное покрытие составляет 180г на 1м2. Хватит ли 5л банки эмали, чтобы покрасить стену длиной 6м и высотой 2,5м?
9. Сторона прямоугольника равна 15см и образует с диагональю угол 30°. Найдите площадь прямоугольника.
10. Середины сторон прямоугольника , если его площадь равна 2.
5. Как изменится площадь и периметр квадрата, если его диагональ увеличить в 4 раза?
6. Постройте квадрат, площадь которого равна сумме площадей двух данных квадратов.
7. Найдите периметр квадрата равновеликого (имеющего равную площадь) прямоугольнику со сторонами 2см и 32см.
8. Расход эмалевой краски на однослойное покрытие составляет 180г на 1м2. Хватит ли 5л банки эмали, чтобы покрасить стену длиной 6м и высотой 2,5м?
9. Сторона прямоугольника равна 15см и образует с диагональю угол 30°. Найдите площадь прямоугольника.
10. Середины сторон прямоугольника 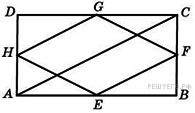 , диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
11*. Как изменится площадь прямоугольника, если две его противолежащие стороны уменьшить в 4 раза, а две другие - в 2 раза.
12* В прямоугольнике , диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
11*. Как изменится площадь прямоугольника, если две его противолежащие стороны уменьшить в 4 раза, а две другие - в 2 раза.
12* В прямоугольнике 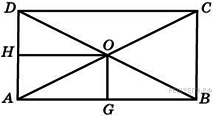 расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.
13*. Четырёхугольник АВСD – квадрат. расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.
13*. Четырёхугольник АВСD – квадрат. 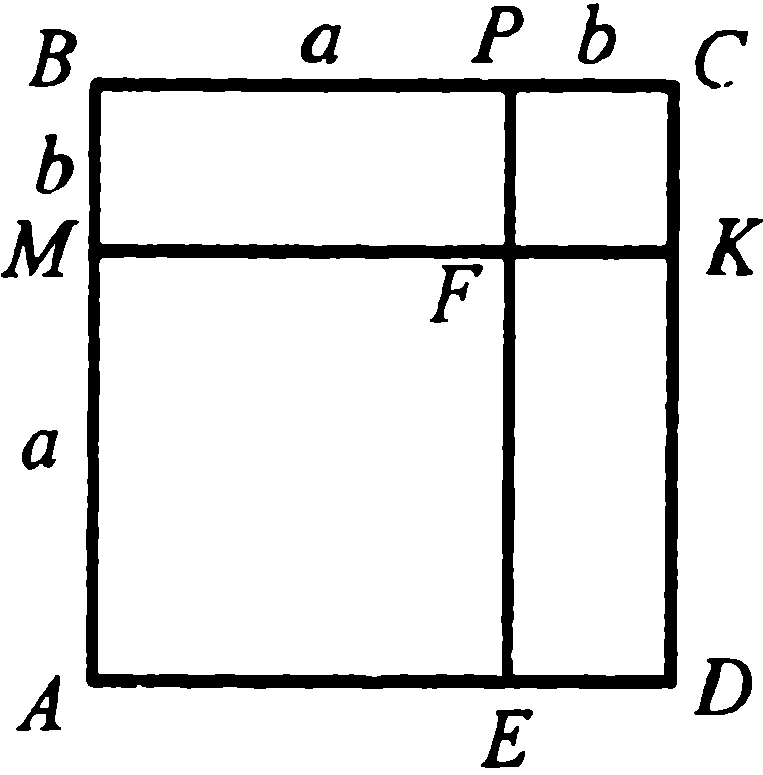 Отрезки МК и РЕ параллельны его сторонам. Пользуясь рисунком, докажите формулу (а + в)2 = а2 + 2ав + в2. Отрезки МК и РЕ параллельны его сторонам. Пользуясь рисунком, докажите формулу (а + в)2 = а2 + 2ав + в2.
|
Список литературы.
1. Алимов Ш.А., Колягин Ю.М. Алгебра 7. – М. «Просвещение» 2010.
2. Алимов Ш.А., Колягин Ю.М. Алгебра 8. – М. «Просвещение» 2010.
3. Атанасян Л.С. Геометрия 7 – 9. М. «Просвещение» 2010.
4. Мерзляк Г.А. Геометрия 7.-М. «Вентана-Граф» 2013.
5. Мерзляк Г.А. Геометрия 8.-М. «Вентана-Граф» 2013.
6. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по алгебре для 7 класса. Харьков. «Гимназия» 2010.
7. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по геометрии для 7 класса. Харьков. «Гимназия» 2010.
8. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по алгебре для 8 класса. Харьков. «Гимназия» 2010.
9. Мерзляк Г.А. Сборник задач и заданий для тематического оценивания по геометрии для 8 класса. Харьков. «Гимназия» 2010.
| <== предыдущая страница | | | следующая страница ==> |
| Математика | | | Функции, заданные параметрически, и их производные |
Дата добавления: 2014-11-24; просмотров: 979; Нарушение авторских прав

Мы поможем в написании ваших работ!