
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Математика
|
Читайте также: |
8 класс
Глейх вадим Антонович – учитель математики, e-mail: spb_sport91@ mail.ru
(отправляя письмо в графе «Кому», указываем «учителю математике Глейху В.А»)
Расписание консультаций: среда 15.00 – 16.00, пятница 15.00 – 16.00.
Критерии оценивания учащихся спортсменов, выполнивших задание. Для получения положительной оценки по итогам четверти учащийся должен:
1) сдать зачёт-минимум по соответствующему предмету:
Алгебра – до 18.12.2014,
Геометрия – до 18.12.2014;
2) сдать учителю в отдельной тетради (12 листов) или прислать по электронной почте по указанному выше адресу в указанные сроки задания и пройти по ним собеседование;
3) написать в классе плановые контрольные работы:
Алгебра: Контрольная работа № 2 до 20.11.2014
Контрольная работа № 3 до 17.12.2014
Геометрия: Контрольная работа № 2 до 10.12.2014.
По итогам выполненного обьёма работ оценки «4 и 5» ставятся за правильно выполненные не менее 70% и 90% заданий соответственно, включая задания (*). Ооценка «3» ставится за правильно выполненные не менее 50% заданий, не включая задания (*)..
Образовательный минимум по алгебре за II четверть.
Теоретическая часть
Таблица квадратов чисел от 11 до 25.
| число | |||||||||||||||
| кв.числа |
Уравнение вида ах2 + вх + с = 0, где а (а ≠ 0), в, с некоторые действительные числа, называется квадратным.
| Решение неполного квадратного уравнения | Решение полного квадратного уравнения | ||
| ах2 = 0 | ах2 + с = 0, с ≠ 0 | ах2 + вх = 0, в ≠ 0 | ах2 + вх + с = 0 , а ≠ 0 |
| х1,2 = 0 |
ах2 = - с
х2 = -  x1 =
x1 = 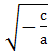 ,
x2 = - ,
x2 = - 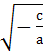 Замечание: -
Замечание: - 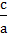 > 0.
- - - - - - - - - - - - - - - -
х2 = d, d ≠ 0
x1 = > 0.
- - - - - - - - - - - - - - - -
х2 = d, d ≠ 0
x1 = 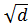 , x2 = - , x2 = - 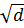 . .
|
х(ах + в) = 0
х = 0, ах + в = 0
х = 0, ах = - в
х1 = 0, х2 = -  . .
|
D = 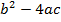 – дискриминант.
х1,2 = – дискриминант.
х1,2 = 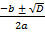 .
Замечание: если D < 0, то исходное уравнение не имеет решений, если D = 0, то - имеет одно решение, если D > 0, то имеет два решения.
Если х1, х2 – корни уравнения ах2 + вх + с = 0,
то при всех х справедливо равенство:
ах2 + вх + с = а(х – х1)(х – х2)
________________________________________
Теорема Виета
Если х1, х2 – корни приведенного квадратного уравнения х2 + pх + q = 0, то
х1 + х2 = - p, х1· х2 = q. .
Замечание: если D < 0, то исходное уравнение не имеет решений, если D = 0, то - имеет одно решение, если D > 0, то имеет два решения.
Если х1, х2 – корни уравнения ах2 + вх + с = 0,
то при всех х справедливо равенство:
ах2 + вх + с = а(х – х1)(х – х2)
________________________________________
Теорема Виета
Если х1, х2 – корни приведенного квадратного уравнения х2 + pх + q = 0, то
х1 + х2 = - p, х1· х2 = q.
|
Практическая часть.
| Вычислить | Сравнить | Упростить | Исключить иррациональность из знаменателя | |||
1) 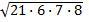 2)
2) 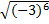 3)
3) 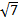 · · 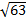 4)
4) 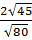
|
5) 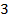 и и 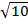 6) 2
6) 2 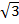 и 3 и 3 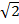
|
7) 3 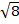 + + 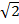 - 3 - 3 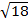 8) (
8) ( 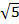 – – 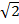 )2
9) (2 - )2
9) (2 - 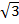 )(2 + )(2 + 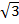 ) )
| 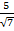 10)
10) 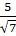 11)
11) 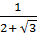
| |||
| Решить неполное квадратное уравнение | Решить квадратные уравнения | Теорема Виета | Разложить на множители | |||
12). х2 = 36
13) х2 = 1  14) х2 = 13
15)
14) х2 = 13
15)  х2 = 0 х2 = 0
| 16) х2 – 121 = 0
17) 4х2 = 81
18) х2 – 27 = 5
19) 25 – 16х2=0
20) 5х2 = 125
21) 4 = 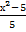
| 22) х2 – 7х = 0 23) 5х2 = 3х 24) 5х + х2 =0 | 25) 2х2 – 3х + 1 = 0 26) 5х2 + 2х + 3 = 0 27) 4х2 + 4х + 1 = 0 28) 10 – 2х + х2= 0 29) 6х2 = 5х + 1 30) х(х – 1) = 72 | 31) х2 + х - 6 = 0 32) х2 + 4х - 5 = 0 | 33) х2 – 5х + 6 34) 2х2 - х - 1 | |
| 35) Периметр прямоугольника равен 1м, а площадь 4дм2. Найти его стороны. 36) Расстояние в 400км скорый поезд прошел на час быстрее товарного. Какова скорость каждого поезда, если скорость товарного поезда на 20 км/ч меньше, чем скорого? 37) сумма двух чисел равна 18, а их произведение 65. Найдите эти числа. | ||||||
Образовательный минимум по геометрии за II четверть.
| Четырёхугольники |
| Параллелограммы Параллелограмм |
| Трапеции |
| Квадраты |
| Прямоугольники |
| Ромбы |
Прямоугольником называется параллелограмм, у которого все углы прямые.
| Свойства прямоугольника. | Признаки прямоугольника. |
| 1.Диагонали прямоугольника равны. | 1.Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник. 2.Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник. |
Ромбом называется параллелограмм, у которого все стороны равны.
| Свойства ромба. | Признаки ромба. |
| 1.Диагонали ромба перпендикулярны, и являются биссектрисами его углов | 1.Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб. |
Квадратом называется прямоугольник, у которого все стороны равны; либо квадратом называется ромб, у которого все углы прямые.
Средней линией треугольника называют отрезок, соединяющий середины
двух его сторон. Средняя линия треугольника: M N
1) параллельна третьей стороне; 2) равна её половине. MN =  a
a
Трапецией называется четырёхугольник, у которого две стороны b
называется четырёхугольник, у которого две стороны
параллельны, а две другие не параллельны. Средняя линия трапеции: M N
1) параллельна основаниям; 2) равна их полу сумме. MN = 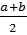 a
a
Площади.
a Квадрат Ромб Прямоугольник Параллелограмм Треугольник Трапеция
b b
a a a a a a S = a2 = 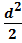 S = S = 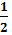 d1·d2 S = a·b S = a·h S = d1·d2 S = a·b S = a·h S =  a·h S = a·h S = 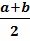 ·h ·h
|
b b
| h |
| h |
| d1 d2 |
| d |
| b |
h
b
a a a a a a
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Дано: АВС – треугольник, АМ = МВ, ВN = NC.
B Доказать: а) МN ǁ AC, б) MN =  AC.
AC.
М N E Доказательство. а) Докажем, что АМЕС – параллелограмм. 1). На прямой МN
отметим точку Е так, что МN = EC, тогда ΔВМN = ΔNЕС ( по I-му признаку).
2) Тогда т.к. ВМ = ЕС и ВМ = АМ (по условию), то ЕС = АМ. 3) < МВN и <NCE
А С (накрест лежащие), то МА ǁ ЕС. Т.о. АМЕС – параллелограмм (по II-му признаку) и следовательно МN ǁ АС. б) 1) т.к. АМЕС – параллелограмм, то МЕ = АС. 2) т.к. МN = 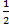 ME, то MN =
ME, то MN =  AC.
AC.
Практическая часть
Прямоугольник.
1. Перпендикуляры опущенные из точки пересечения диагоналей прямоугольника на две его соседние стороны равны 5см и 7см. Найдите периметр прямоугольника.
2. Докажите, что в прямоугольном треугольнике медиана, проведённая из вершины прямого угла равна половине гипотенузы.
3. В прямоугольнике АВСD 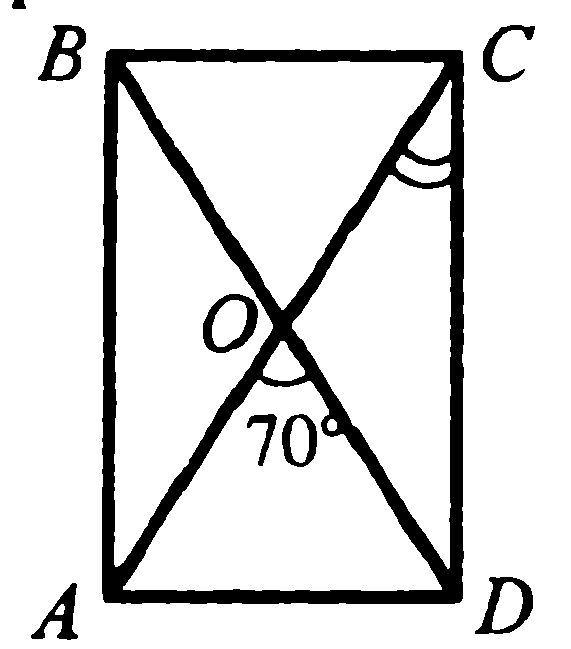 О – точка пересечения диагоналей. <АОD = 70°. Найдите угол OСD.
О – точка пересечения диагоналей. <АОD = 70°. Найдите угол OСD.
Ромб
4. Докажите, что если две соседние стороны параллелограмма равны, то он является ромбом.
5. АВСD - ромб 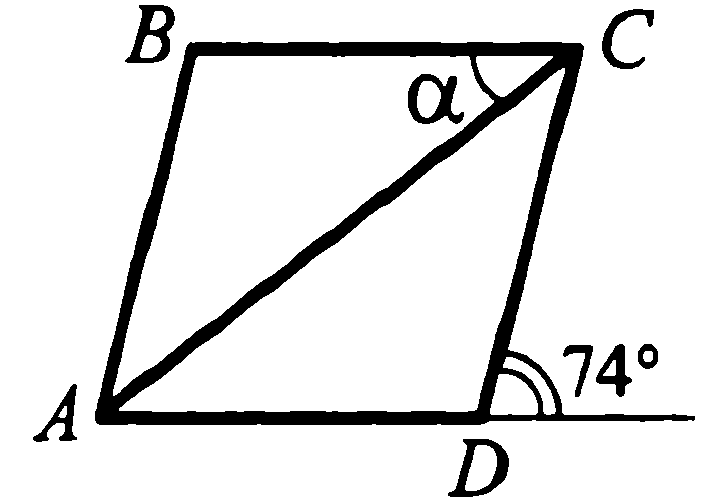 Найдите угол α.
Найдите угол α.
6. В ромбе АВСD известно, что <С = 140°, а диагонали пересекаются в точке О.Найдите углы ΔАОВ.
Квадрат
7. Диагональ квадрата равна 4см. Его сторона является диагональю второго квадрата. Найдите сторону второго квадрата.
8. Постройте квадрат, если известно что его периметр равен 24см.
Средняя линия треугольника
9. Стороны треугольника равны 6см, 8см и 12см. Найдите средние линии этого треугольника.
10. Докажите, что средние линии треугольника разбивают его на четыре равных треугольника.
11. Средняя линия равнобедренного треугольника, параллельная основанию равна 6см. Найдите стороны.
Трапеция. Средняя линия трапеции.
12. Периметр трапеции равен 49см, боковые стороны – 5,6см и 7,8см. Найдите основание трапеции, если одно из них на 7,7см больше другого.
13. В равнобедренной трапеции угол между боковой стороной и высотой, поведенной из вершины тупого угла, равен 23°. Найдите углы трапеции.
14. Средняя линия трапеции равна 8см, а одно из оснований – 5см. Найдите второе основание трапеции.
15. Через вершину С трапеции АВСD проведена прямая, которая параллельна боковой стороне АB и пересекает большее основание АD в точке Е. ВС = 8см, ЕС = 5см. Найдите среднюю линию трапеции АВСD.
Площадь прямоугольника и квадрата.
16. Найдите площадь прямоугольника ABCD, 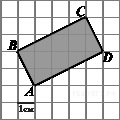 считая стороны квадратных клеток равными 1.
считая стороны квадратных клеток равными 1.
17. Найдите площадь прямоугольника  , если его периметр равен 18, и одна сторона на 3 больше другой.
, если его периметр равен 18, и одна сторона на 3 больше другой.
18. Найдите диагональ квадрата 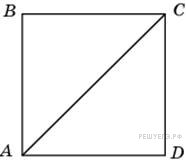 , если его площадь равна 2.
, если его площадь равна 2.
19. Как изменится площадь и периметр квадрата, если его диагональ увеличить в 4 раза?
20. Середины сторон прямоугольника 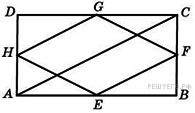 , диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
, диагональ которого равна 5, последовательно соединены отрезками. Найдите периметр образовавшегося четырехугольника.
Алгебра
| Задание 4(а). Действия с арифметическим квадратным корнем. (см. Алимов 8. Гл.III, § 22-24). Сдать до 18.11.2014 1. № 329(1), 331(4), 332(2), 334(2), 335*(4), 336*(2) 2. № 340(2), 341(4), 342(4), 343(4),344(2), 345(2), 346(2), 347(4), 348(4), 349(2), 350(2), 351(3), 352(1) 354(2), 355*(2), 357*(1),358*(2), 361*(2). 3. № 362(2), 363(2), 364(4), 365(4), 366(2,6), 369(2), 371*(2,4), 373*(2,4),376*(2). | Задание 6(а). Решение квадратных уравнений. (см. Алимов 8. Гл.IV, § 28). Сдать до 6.12.2014 1. № 429*(2,4,6). 2. № 433(3), 438(2,4), 434(2.4,6), 436(2,4), 437(2,4), 439(2,6), 440(2,4), 440*(6),441*(2,4), 442*. |
| Задание 7(а). Теорема Виета. Уравнения, сводящиеся к квадратным. (см. Алимов 8. Гл.IV, § 29, § 30). Сдать до 13.12.2014 1. № 450(2,4,6), 456(2,4,6), 455(2,4), 457(2,4,6,8), 458(4,6), 459*(2), 460*(4), 461*(4), 462*(2,4), 466*(1). 2. № 468(2), 469(4), 470(2), 471(2), 471*(4), 474*(2). | |
| Задание 5(а). Неполные квадратные уравнения. (см. Алимов 8. Гл.IV, § 25-27). Сдать до 29.12.2014 1. № 402(4,6), 403(2), 407(3,6), 408(3,6), 417(2,3), 419(5,6). 2. № 409(2,6), 417(5,6), 410(3,6), 412*(2). 3. № 417(2,3.5). 4. № 418(5,6), 419(2), 420(2,4), 404(2,4), 406(2,5), 421*(2,4), 423*(2), 427*(2). | Задание 8(а). Решение задач с помощью квадратных уравнений. (см. Алимов 8. Гл.IV, § 31). Сдать до 20.12.2014 1. № 477, 478, 480, 481, 482, 483*, 484*, 485*, 486*, 491*. |
| Задание 9(а). Решение простейших систем, содержащих уравнение второй степени. (см. Алимов 8. Гл.IV, § 31). Сдать до 18.12.2014 1. № 492(4) – 497(4), 501*(2,4,6), 502*(2,4), 503*(2). 2. № 498, 499, 504*, 507*. | |
Диагностическая контрольная работа № 3.
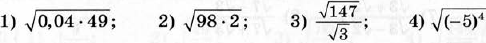
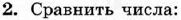
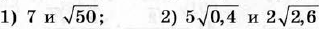
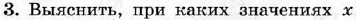
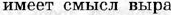  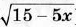
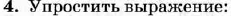
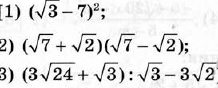
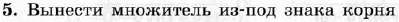
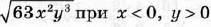
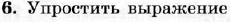
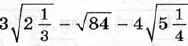
| Диагностическая контрольная работа № 4.
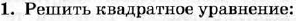

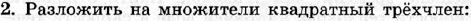


 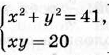

|
| <== предыдущая страница | | | следующая страница ==> |
| Ранние постдеполяризации | | | Геометрия |
Дата добавления: 2014-11-24; просмотров: 500; Нарушение авторских прав

Мы поможем в написании ваших работ!