Математика на средневековом Востоке

(-СН₂-СН-)_n (-СН₂-С=СН-СН₂-)_n

I

СНз

- полибутадиен типа СКД (-СН₂-СН=СН-СН₂-)_П

и др.

По энергетическим свойствам все горючие-связующие подразделяют на "активные" и "инертные". Такое разграничение в значительной степени является условным.

К "инертным" принято относить ГСВ, в которых окислительные элементы либо полностью отсутствуют (например, бутилкаучук), либо их содержание значительно меньше, чем горючих элементов (например, полиуретановый каучук), а энтальпия образования отрицательная.

К "активным" относят ГСВ, обогащенные окислительными элементами и способные к самостоятельному горению в инертной среде, а также ГСВ имеющие положительную энтальпию образования. Наиболее благоприятным является сочетание повышенного содержания окислительных элементов с положительной энтальпией образования, что на практике встречается крайне редко. Примером связующего, обогащенного окислительными элементами, может быть композиция нитратов целлюлозы с нитроглицерином. Примером высокоэнтальпийного связующего являются композиции на основе органических азидов, триазолов, тетразолов.

Топлива на основе "активного" ГСВ характеризуются более высоким удельным импульсом и плотностью. Применение "активных" связующих также сдвигает оптимум в содержании ГСВ в топливе в область повышенного количества, что приводит к улучшению технологических, механических и других характеристик СТТ.

Химическая природа связующих проявляется также в их структуре и влиянии ее на механические и другие свойства топлив. В зависимости от величины межмолекулярного взаимодействия и соответственно температуры стеклования (температурный диапазон, при котором полимер теряет эластичность, и становится как стекло) полимеры, составляющие основу ГСВ, подразделяют на эластомеры (каучуки) и пластики.

Так, заряды на основе эластомеров находятся в высокоэластическом состоянии, а заряды на основе пластиков – в стеклообразном. Высокий уровень деформационных характеристик СТРТ на основе эластомеров позволяет изготавливать заряды, скрепленные с корпусом двигателя. И напротив - низкий уровень деформируемости СТРТ в стеклообразном состоянии обусловливает применение, как правило, вкладных зарядов, которые могут быть менее эффективны, чем скрепленные.

Классификация СТТ может быть проведена на основе химической природы металлического горючего. В соответствии с тем, что к настоящему времени в составах СТТ различного назначения используют преимущественно алюминий и магний, выделяют алюминий- и магнийсодержащие топлива. В отдельных случаях используют сплавы алюминия с магнием. За рубежом велись разработки и бериллийсодержащих СТТ, отличающихся более высоким удельным импульсом. Однако вследствие высокой токсичности оксидов бериллия и соответственно экологической опасности продуктов сгорания эти топлива практически не используют.

Наряду с А1 и Mg-содержащими СТТ разработаны составы с бором и борсодержащими горючими.

Анализ современных составов ТРТ показывает, что строгой границы между гомогенными (нитроцеллюлозными) и гетерогенными (смесевыми) твердыми топливами не существует. Классические нитроцеллюлозные пороха лишь условно можно считать гомогенными. Последующие их модификации и прежде всего модификация баллиститных ТРТ в целях повышения энергетических и других характеристик превратили их в многофазные гетерогенные системы.

Математика на средневековом Востоке.

План.

1. Зарождение и распространение новой религии – ислама. Арабский халифат.

2. Багдадская математическая школа. Мухаммад ибн Муса аль-Хорезми (ок. 783-ок. 850) и его математические труды.

3. Историческая обстановка и развитие науки в арабоязычных государствах начиная с X в.

4. Абу Райхан Бируни (973-ок. 1050) и его научные труды.

5. Омар Хайям (ок. 1048-1131) – великий поэт и учёный Востока.

6. Марагинская математическая школа. Насирэддин ат-Туси (1201-1274).

1. В конце V в. западная Римская империя пала, разрушенная восстаниями рабов и завоеваниями «варваров», т.е., в основном, германских племён. На этом закончилась история древнего мира и началась история средних веков. Восточная римская империя с центром в Византии тем временем продолжала существовать и достигла наибольшего расцвета в VI в. при императоре Юстиниане.

В истории средневековья выделяют:

· раннее средневековье – VI-X вв.

· собственно средние века – XI-XIV вв.

Эпохой Возрожденияили Ренессансом называют XV-XVI века, однако существует термин «раннее Возрождение», относящийся ко времени на рубеже XIII-XIV веков. Это время также называют периодом Итальянского Возрождения. Особенно часто этот термин применяют в истории искусства.

С периодом буржуазных революций в Англии (1640-1660 гг.) в истории человечества начинается новый период, который так и называется - Новое время.

XVIII век часто называют веком Просвещенияили временем Французского Просвещения.

Раннее средневековье для европейской науки, в особенности для математики, было периодом забвения и гонений. Деятельность математиков смешивалась с деятельностью язычников, а также разнообразных магов, звездочётов и колдунов, с которыми ещё в Римской империи велась непримиримая борьба.

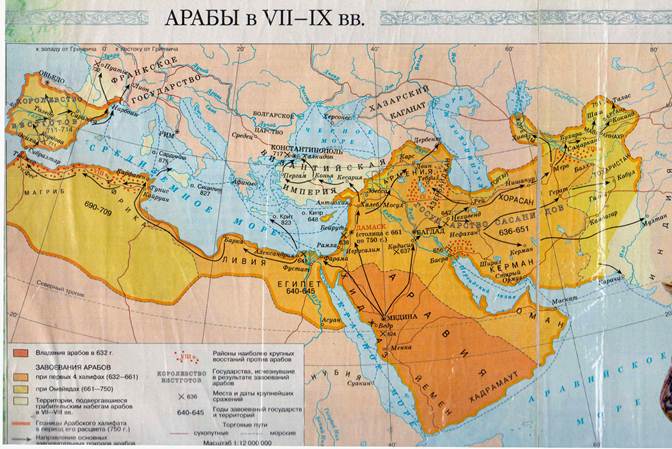
В VII веке родилась и быстро объединила народы арабоязычного Востока новая религия – ислам. Её основатель, пророк Мухаммад (570-632 гг.) начал проповедовать основы ислама около 610 года. Идеи пророка новой религии распространялись очень быстро, и скоро они объединили народы, населявшие Аравийский полуостров, территория которого равна почти четверти территории Европы. С помощью ислама арабы объединились в мощное государство, во главе которого встали «заместители» пророка - халифы. К концу столетия арабы завоевали Сирию, Междуречье, Иран, Египет, Среднюю Азию. Позднее им подчинились Испания, Сицилия, юг Италии, часть Закавказья, часть Индии. Образовалось новое обширное исламское государство – арабский халифат.Господствующим языком государства был арабский, столицей стал сначала Дамаск, а с VIII века – новый город, Багдад, построенный вблизи бывшего Вавилона.

Управление новым государством требовало быстрого развития торговли, промышленности, военного дела, а огромные территории – знаний в области географии и астрономии. Астрономия вообще оказалась одной из самых нужных в странах ислама наук. Астрономических знаний требовали и особенности религии. Ведь правоверный мусульманин должен в строго определённые часы пять раз в сутки совершать намаз (молитву), стоя при этом лицом к священному городу Мекке. Поэтому, где бы ни находился человек, он должен пять раз в сутки точно определить время и направление сторон света. Если учесть, что огромные пространства требовали длительных путешествий по пустыне, то станет понятно, насколько необходимы были знания о небесных светилах, причём нуждались в этих знаниях не только учёные.

После 761 г. мир ислама перенял у китайцев способ изготовления бумаги, и это существенно ускорило распространение научных знаний в государстве.

Перечислим основные научные центры арабоязычного мира.

· Багдад.

· Бухара, Самарканд, Хорезм (Средняя Азия).

· Исфахан (Пакистан).

· Газна (Афганистан).

· Марага (Азербайджан).

· Каир (Египет)

2. В качестве основных математических школ у мусульманских народов VII-XV вв. можно выделить три: Багдадскую, Марагинскую и Самаркандскую.

Город Багдад был основан в 60-е годы VIII в. халифом аль-Мансуром, который правил с 754 по 775 гг. Новая столица государства быстро сделалась важным центром торговли, науки и культуры. Город отличался оригинальной планировкой. Он имел форму круга с диаметром около двух километров. Его окружала двойная крепостная стена с четырьмя воротами, направленными на север, юг, восток и запад.

Багдадская школа является первой научной школой арабоязычного Востока. Особое внимание здесь уделялось изучению достижений античной и эллинистической науки. Сочинения греческих классиков собирались и переводились на арабский язык. Для покупки рукописей снаряжались специальные экспедиции. Особый интерес вызывали труды по астрономии, геодезии, картографии и по математике – основе этих наук. Одними из первых были переведены «Начала» Евклида, «Сферика» Менелая, «Альмагест» Птолемея. Изучались также индийские астрономические сочинения.

Однако багдадские учёные были не только переводчиками и комментаторами. Они достигли замечательных успехов и в самостоятельных научных исследованиях разнообразной направленности. Преемники халифа Аль-Мансура продолжали оказывать покровительство науке. Его внук Харун ар-Рашид известен (правда, в идеализированном виде) по «Сказкам тысячи и одной ночи». Наибольшего расцвета наука в Багдаде достигла при сыне Харуна ар-Рашида халифе аль-Мамуне, правившем с 813 по 833 гг. (Напомним, что именно этот халиф приказал разграбить гробницу Хеопса.) При нём в Багдаде был основан так называемый «Дом мудрости» – учреждение, выполнявшее функции Академии наук (вспомните Мусейон в Александрии). При Доме Мудрости находилась богатейшая библиотека старинных рукописей и астрономическая обсерватория. Для работы там халиф приглашал наиболее выдающихся учёных. В их числе был и Мухаммад ибн Муса аль-Хорезми, который стал заведовать багдадской библиотекой. Он был родом из Хорезма, то есть из Средней Азии, о чём говорит последняя часть его имени – нисба«аль-Хорезми».

Рисунок . Почтовая марка, выпущенная в СССР в 1983 году по случаю 1200-летнего юбилея аль-Хорезми.

Средняя Азия с VIII в. входила в состав арабского халифата, но уже через столетие она от него фактически отделилась. До распространения ислама на этой территории располагались государства Бактрия, Согдиана, древний Хорезм, обладавшие высокой культурой. Арабы, насаждая мусульманство, жестоко расправились с представителями этой культуры, но не могли не воспользоваться многими её достижениями

Хорезм – район Средней Азии, который в наши дни входит в состав Узбекистана, центр Хорезма – город Ургенч.

Аль-Хорезми родом из Хорезма, но более точно место его рождения не установлено. В некоторых источниках он назван «аль-маджуси», т.е., маг, и из этого заключают, что предки его были магами, жрецами зороастрийской религии, которая была распространена на территории Средней Азии до ислама. Известно, что образование ал-Хорезми получил в крупном городе восточного региона халифата – Мерве. В Багдад он приехал после 818 г.

Об обстоятельствах жизни аль-Хорезми известно немного. Установлено, что он был автором девяти научных трудов, из которых до наших дней сохранилось семь. Эти труды, а также упоминания о них в средневековой литературе, позволяют судить о разнообразии научных интересов учёного. Назовём наиболее известные его математические и астрономические трактаты.

· «Арифметический трактат».

· «Алгебраический трактат».

· «Извлечения из астрономических таблиц индийцев».

· «Книга о построении астролябии».

· «Книга о солнечных часах».

«Арифметический трактат» сыграл важнейшую роль в истории математической науки. В нём впервые была систематически изложена арифметика целых чисел, основанная на десятичной позиционной системе счисления с нулём.Эта система счисления, как Вы знаете, возникла в Индии. Поэтому и Хорезми называл её индийской. Она долго не выходила за пределы Индии и только благодаря «Арифметическому трактату» получила широкое распространение в странах Ближнего и Среднего Востока, а затем (лишь в XII веке) и в Европе. Подчеркнём, что в этом трактате ещё не идёт речи о десятичных дробях. Учёные средневекового Востока до XV века пользовались шестидесятеричными дробями вслед за Птолемеем.

«Алгебраический трактат» аль-Хорезми имел заглавие «Краткая книга восполнения и противопоставления» – «Китаб мухтасар ал-джабр ва-л-мукабала». В этом трактате впервые алгебра рассматривается как самостоятельный раздел математики– наука об уравнениях. В нём изложены правила решения уравнений первой и второй степени с числовыми коэффициентами. Все такие уравнения сведены были к шести каноническим типам:

1.

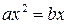
2.

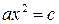
3.

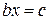
4.

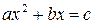
5.

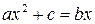
6.

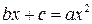
Как Вы думаете, почему было выделено так много типов линейных и квадратных уравнений? Ведь в современной элементарной алгебре такой классификации нет, она не нужна!

Для приведения уравнения к каноническому виду вводились две операции. Операция ал-джабр (восстановление)состоит в избавлении от членов уравнения со знаком «минус» в одной части уравнения путём прибавления к обеим его частям одинаковых слагаемых. Ясно, что она равносильна нашему перенесению какого-либо члена уравнения из одной части в другую с противоположным знаком.

Вторая операция – аль-мукабала (противопоставление)состоит в удалении одинаковых членов из обеих частей уравнения, или во взаимном уничтожении равных по абсолютной величине членов уравнения с противоположными знаками.

Заметим, что все эти уравнения описывались словесно, так как символического языка алгебры ещё не существовало. Например, вместо уравнения 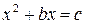писалось: «Квадрат с вещами равен числу». Словесно описывались и правила решения уравнения каждого типа.

В латинском переводе слово «ал-джабр» приобрело форму «алгебра» и стало впоследствии названием раздела математики и целой математической науки. Добавим, что латинизированное имя аль-Хорезми (Алгоризми) превратилось в слово «алгоритм» и стало обозначать порядок любого вычислительного процесса.

С помощью этих двух операций Аль-Хорезми сводил всякое уравнение первой или второй степени к одному из шести типов, добиваясь, чтобы все коэффициенты уравнения были положительными, а коэффициент при неизвестном во второй степени становился единицей, например:

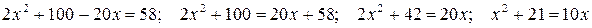(пятый тип). Для каждого типа было изложено правило решения. Хорезми редко пользовался иррациональными величинами. Иррациональный корень уравнения он называл «джизр ассам», т.е. «глухой корень». В XII веке знаменитый испанский переводчик арабских трудов на латынь Герардо Кремонский точно перевел слово «ассам» латинским словом «surdus», т.е. глухой, и до XVIII века в Европе иррациональные числа также назывались глухими.

3. К началу X века завоёванные арабами страны, сохраняя религиозное подчинение Багдаду, становятся фактически независимыми. Образуется несколько новых государств:

· Держава Саманидов со столицей в Бухаре. Она объединяла Хорасан (нынешняя Туркмения и часть Ирана) и Мавераннахр (междуречье Сыр-Дарьи и Аму-Дарьи).

· Хорезм (Хорезмская область с центром в Ургенче, север Туркмении и Каракалпакии).

· Государство Буидов (центральный Иран и Месопотамия).

Позднее буиды подчинили себе багдадских халифов, а в Северной Африке и Испании возникли новые независимые халифаты со столицами в Каире и Кордове.

В середине X века Мавераннахр завоевали тюрки-илекханы, а центральный Иран. Хорасан и Хорезм подчинились афганскому завоевателю Махмуду Газневи, который основал огромную империю со столицей в Газне.

B XI веке Среднюю Азию, Иран, Сирию, Месопотамию завоевали тюрки-сельджуки, которые, как ранее буиды, подчинили себе багдадского халифа.

В XIII веке все эти территории были покорены монголами. В 1258 г. они убили последнего халифа и окончательно ликвидировали арабский халифат.

В XV веке Среднюю Азию, Иран и ряд сопредельных государств завоевали войска Тимура. Столицей его владений с конца XIV века стал город Самарканд.

Несмотря на столь неспокойную историческую обстановку, несмотря на постоянные войны, государства средневекового Востока уже не могли существовать без развития науки. Об этом свидетельствует тот факт, что на протяжении всех этих шести веков (X-XV) наука в этих странах не только не погибала, но продолжала развиваться, на территории упомянутых государств возникали всё новые научные центры. История науки средневекового Востока знает много замечательных имён. Мы только в общих чертах познакомимся с творчеством крупнейших учёных X-XV веков.

Рисунок . Почтовая марка, выпущенная в СССР в 1973 году по случаю 1000-летнего юбилея аль-Бируни.

4. В начале X века крупнейшие научные центры возникли в Бухаре и Хорезме. Именно здесь получили образование и работали два замечательных учёных этого времени – Абу Райхан аль-Бируни (973-1050)и Ибн Сина (Авиценна) (980-1037), известный прежде всего как один из классиков медицинской науки. Следует, однако, заметить, что и ему принадлежит несколько математических трудов, например, комментарии к «Альмагесту» Птолемея и «Началам» Евклида. Судьба этих учёных, которые были не только знакомы, но и дружны между собой, оказалась во многом схожей.

Абу Райхан Мухаммад ибн Ахмад аль-Бируни был очень незнатного происхождения. По-видимому, нисба «аль-Бируни» означает «человек из предместья». Он, действительно, родился в предместье города Кят. Ныне это город Бируни в Каракалпакии, а в X веке это была столица Хорезма. В предисловии к одному из своих трудов сам Бируни писал, что не помнит своего отца, а мать была носильщицей дров. Это, по-видимому, значит, что он был сыном бедной вдовы. В другом труде он тепло вспоминал человека, который научил его распознавать лекарственные растения. Похоже, что это был пленный европеец, учёный, врач, щедро делившийся с любознательным мальчиком своими знаниями.

Любознательностью Бируни, вероятно, отличался с детства, а потому вызывал у образованных людей интерес и желание учить способного юношу. Главным его учителем стал выдающийся среднеазиатский астроном и математик Абу Наср Мансур ибн Али ибн Ирак (ок. 960-ок. 1035 гг.). О нём Бируни говорил как о наставнике и воспитателе, которому обязан всем.

Ибн Ирак родился в Хорезме и находился в родстве с хорезмскими правителями. Научную деятельность он начал в Кяте. Ему принадлежит более 20-ти сочинений по астрономии и математике, оказавших сильное влияние на современных ему учёных и на науку более позднего времени. Например, «Сферика» Менелая впервые стала известна в Европе именно в переводе Ибн Ирака и с его комментариями.

Бируни, вероятно, благодаря Ибн Ираку, уже к 17-ти годам стал образованным человеком. Во всяком случае, известно, что в этом возрасте он уже занимался вместе со своим учителем астрономическими наблюдениями. Ибн Ирак был близок ко двору правителя Хорезма, а поэтому и Бируни начинал свою научную деятельность при дворе этого правителя. Однако такая близость не всегда шла на пользу учёным. Бурные политические события, в которых участвовали правители, не могла не отразиться на судьбе близких этим правителям людей. Кроме того, и отношения с самими правителями иногда становились сложными.

В 990-х годах правящая династия хорезмских правителей пала в одной из междоусобных войн, и Бируни пришлось бежать из Хорезма. Он перебрался в город Рейблиз Тегерана и работал там около восьми лет, затем переселился в Гурган, столицу одноименного княжества на юго-восточном побережье Каспийского моря, и прожил там около шести лет. В 1004 г. вернулся в Хорезм по приглашению нового правителя. Более или менее спокойный период его жизни продолжался до 1017 г. В это время в Хорасане и Афганистане укрепилась власть Махмуда Газневи, и в конце концов он подчинил себе и Хорезм. Бируни вместе со своим учителем ибн Ираком был взят в плен и вынужден переехать в Газну на юго-востоке Афганистана, где и работал уже до конца своей жизни.

При сыне Махмуда Газневи, султане Масуде, ему жилось и работалось несколько лучше и свободнее, чем при самом Махмуде. В благодарность за покровительство Бируни именно султану Масуду посвятил свой наиболее значительный научный труд – «Канон Масуда по астрономии и звёздам» (1036 г.). Этот труд представляет собой свод астрономических знаний средневекового Востока, за который Бируни называют Восточным Птолемеем.

Это был учёный разносторонних интересов и энциклопедических знаний в области географии, геологии, физики, ботаники, минералогии, этнографии, истории. В математике его особенно интересовали вопросы арифметики, алгебры, геометрии, тригонометрии, теории чисел.

Кстати, говоря о вкладе восточных математиков в теорию чисел, необходимо отметить, что в их трудах вместо двух обособленных понятий – числа и отношения двух чисел – которые были у греков, впервые возникает новая, более широкая трактовка числа как отношения двух целых чисел, то есть разрабатывается концепция рационального числа, близкая к современной.

Среди сохранившихся трудов Бируни нет сочинений, специально посвящённых вопросам алгебры, но в трактате «Наука звёзд» формулируются основные определения и правила алгебры, а в «Каноне Масуда» приводятся некоторые способы численного решения кубических уравнений.

2. Омар Хайям (ок. 1048-1131)родился в Хорасане, в древнем городе Нишапуре,в семье зажиточного ремесленника. Он учился в городе Балхе, а в 70-х гг. XI в. поселился в Самарканде.

Омар Хайям знаменит прежде всего как поэт. Его перу принадлежит около 400 четверостиший на персидском языке – знаменитые «Рубаи». Но, кроме того, Хайям – автор ряда философских работ, а также относится к крупнейшим астрономам и математикам Востока. Первые его труды по математике, в том числе комментарии к «Началам» Евклида, прославили его, и он был приглашён ко двору правителя Бухары.

Рисунок . Обложка сборника четверостиший Хайяма изд. 1978 г.

К этому времени стремительно возросла и утвердилась огромная империя Великих Сельджуков – выходцев из кочевого туркменского племени Огузов. В 1055 г. сельджукский султан Торгун-бек завоевал Багдад и объявил себя духовным главой всех мусульман. При следующем султане Мелик-шахе империя Великих Сельджуков простиралась от границ Китая до Средиземного моря, от Индии до Византии.

Омар Хайям в 1074 г. был приглашён в столицу нового государства Исфахан.Здесь он стал почётным приближённым султана. Ему было поручено строительство обсерватории, которую он затем возглавил. Под его руководством в этой обсерватории были составлены новые астрономические таблицы и проведена реформа календаря.

В 1092 г. Мелик-шах умер, началась ожесточённая борьба за власть, в результате которой империя сельджуков стала распадаться на отдельные государства. Деятельность научного центра в Исфахане прекратилась. Отношения Омара Хайяма с наследниками Мелик-шаха были не очень хорошими, и постепенно он удалился от двора правителей, предпринял паломничество в Мекку, некоторое время жил в Багдаде, а последние годы жизни провёл на родине, в Хорасане.

Основной математический труд Хайяма – «Комментарий к трудностям во введениях книги Евклида» (1077 г.). В этом сочинении исследуется теория отношений и учение о числе. Кроме того, Хайям пытался доказать пятый постулат Евклида. В результате этих попыток он, по сути дела, доказал первые теоремы геометрий Лобачевского и Римана.

Рисунок . Страница рукописи Хайяма «Комментарии к трудностям во введениях книги Евклида».

«Трактат о доказательствах задач алгебры и алмукабалы» (ок. 1069 г.)посвящён классификации и решению уравнений выше второй степени. Хайям решал уравнения третьей степени геометрическими методами.

Отметим также его трактат «Об искусстве определения количества золота и серебра в состоящем из них теле». В нём находят развитие размышления Архимеда о короне Гиерона.

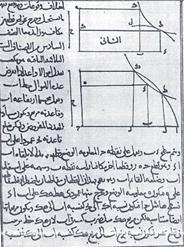
Рисунок . Страница алгебраического трактата Хайяма.

3. В XIII в. Среднюю Азию, Иран, Сирию, Месопотамию завоевали монголы. Крупнейший математик этого времени Насир-эд-дин ат-Туси (1201-1274) – уроженец г. Туса в Хорасане. В 50-х гг. XIII в. он работал в Кухистане (северо-восток Ирана), в столице государства, управлявшегося террористической сектой ассасинов (убийц), которые воевали с множеством врагов. Их врагами были как багдадские халифы, так и европейские крестоносцы, но, в конце концов, в 1253 г. их столицу завоевали монголы. После этого ат-Туси перешёл на службу к монгольскому хану Хулагу, внуку Чингисхана. По совету Туси Хулагу-хан организовал в своей столице Мараге (южный Азербайджан) астрономическую обсерваторию, куда привлекали для работы учёных из всех стран, захваченных к этому времени монголами. Таким образом и возникла так называемая Марагинская школа.

Насир-эд-дин ат-Туси перевёл с греческого на арабский язык и снабдил комментариями и добавлениями важнейшие математические, астрономические, физические труды древних авторов: «Начала», «Феномены» и «Оптику» Евклида, «Об измерении круга» и «О шаре и цилиндре» Архимеда, «Альмагест» Птолемея, «Конические сечения» Аполлония и «Сферику» Феодосия. Он составил комментарии к книге «Шмарат» («Обозначения») Ибн Сины (Авиценны). Из его собственных трудов назовём книги «Шакл-ул-Кита», посвящённую сферической тригонометрии и теории отношений, «Каванд-ул-Хандаса» (трактат по геометрии) и «Таэкира» (трактат по астрономии).

Ещё в юности на Насир-эд-дина ат-Туси большое впечатление произвел геометрический труд Омара Хайяма «Комментарий к трудностям во введениях книги Евклида». До наших дней сохранились две редакции «Тахрир Уклидас» – перевода «начал» Евклида с комментариями и добавлениями Насир-эд-дина. Учёный предпринял очередную попытку доказать пятый постулат Евклида. Первая из двух упомянутых редакций, содержащая 13 книг, была напечатана в Риме в 1594 г. на арабском языке. Вторая содержит 15 книг (две добавлены комментаторами «Начал»). Она была издана также в Риме в 1657 г. в переводе на латынь. С этими изданиями были знакомы английский математик Джон Валлис (1616-1703 гг.) и итальянский учёный Джованни Саккери (1667-1733 гг.), труды которых, в свою очередь, сыграли важную роль в предыстории неевклидовой геометрии.

Вопросы к семинару «Математика на средневековом востоке»

1. Изложите вкратце историю возникновения ислама и Арабского халифата, а также постепенного распада этого государства.

2. Что Вы можете рассказать о развитии науки в средневековых арабоязычных государствах?

3. Расскажите о научной деятельности ал-Хорезми и значении его арифметического и алгебраического трактатов для развития математической науки.

4. Расскажите о наиболее значительных учёных стран арабоязычного Востока в X – XV веках.

5. Расскажите о роли математиков арабоязычного Востока в предыстории создания неевклидовой геометрии.

Рекомендуемые темы для рефератов и сообщений.

1. «Арифметический трактат» ал-Хорезми.

2. «Алгебраический трактат» ал-Хорезми.

3. Геометрия в трудах ал-Хорезми.

4. Омар Хайям – поэт и учёный.

Литература по теме.

1. Сираждинов С.Х., Матвиевская Г.П. Ал – Хорезми – выдающийся математик и астроном средневековья: пособие для учащихся. – М.: Просвещение, 1983. – 78 с.

2. Юшкевич А.П. Омар Хайям и его «Алгебра»./ Труды Института истории естествознания, 1948, 2.

3. Омар Хайям. Трактаты. Перевод Б.А.Розенфельда. Вступительная статья и комментарии Б.А.Розенфельда и А.П.Юшкевича. – М.: Изд. Восточной литературы, 1961. – 338 с.

4. Розенфельд Б.А., Рожанская М.М., Соколовская З.К. Абу-р-Райхан ал-Бируни. – М.: Наука, 1973. – 271 с.

5. Сираждинов С.Х., Матвиевская Г.П. Абу Райхан Беруни и его математические труды: пособие для учащихся. – М.: Просвещение, 1978. – 95 с.

Дата добавления: 2014-05-17; просмотров: 1303; Нарушение авторских прав

Мы поможем в написании ваших работ!