
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ «Дискретная математика»
Направление подготовки 230100 «Информатика и вычислительная
техника»
Профиль подготовки «Автоматизированные системы обработки
информации и управления».
Квалификация (степень)
выпускника Бакалавр
Форма обучения очно-заочная
| |
| |
Курс 2, семестр 4
Объём учебных занятий в часах:
Аудиторные занятия: лекции – 36, практика – 18, всего 54 ч.;
Самостоятельная работа: 110 ч.;
Общий объём курса – 164 ч.
Трудоёмкость 6 ЗЕТ, 5,5 кредитов.
Форма отчётности – Экзамен
Группы – направления подготовки – 230100 "Информатика и вычислительная
техника"
Индекс дисциплины в Рабочем учебном плане (РУП) и в Компетентностно-ориентированном учебном плане (КОП) – Б2.В.3
Естественно-научный модуль – ЕН.Б2
Учебную программу составил ст. преподаватель каф. ВМ НТИ НИЯУ МИФИ Орлов Юрий Владимирович
Учебная программа рассмотрена на заседании кафедры "Высшей математики"
НТИ НИЯУ МИФИ и рекомендована для подготовки бакалавров
"______" ________________ 20 ____ г.
.
Заведующий кафедрой _________________________ Н.А.Носырев
_________________________ 20 ____ г.
СОГЛАСОВАНО
Заведующая библиотекой __________________________ С.У. Иванова
__________________ 20 _____ г.
1 Цели освоения учебной дисциплины
Целью освоения учебной дисциплины "Дискретная математика", как дисциплины математического цикла, является воспитание достаточно высокой математической культуры, развитие у студентов широкого кругозора в области математики и умения использовать математические методы для решения практических задач.
2 Место учебной дисциплины в структуре ООП ВПО
Данная учебная дисциплина входит в Естественнонаучный образовательный модуль раздела Б2 «Математический и естественнонаучный цикл», в его раздел Б2.В.3 ФГОС-3 по направлению подготовки ВПО 230100 "Информатика и вычислительная техника" профиля подготовки бакалавров "Автоматизированные системы обработки информации и управления".
Данный курс является подготовительным для спецкурсов, использующих методы дискретной математики («Дискретизация информации», «Математические основы обработки сигналов», «Элементы цифровых электронных схем цепи и микросхемотехника» и т.д.). Курс читается в 4 семестре, перед этим уже рассмотрен курс «Математика» из 3 семестров. В четвёртом семестре вместе с данным курсом изучается курс «Теория вероятностей и математическая статистика», в котором многократно используются знания из этого курса.
Данная дисциплина участвует в формировании следующих общепрофессиональных компетенций:
КМ.ОК.0.1-2, КМ.ОК.0.9-10, КМ.П.ОП.0.1, КМ.П.ПР.1.2, КМ.П.НИ.1.16
- Способность владеть культурой мышления, способность к обобщению, анализу информации, постановке цели и выбору путей её достижения (КМ.ОК.0.1.)
- Умение логически верно, аргументировано и ясно строить устную и письменную речь (КМ.ОК.0.2 )
- Способность анализировать социально-значимые проблемы и процессы (КМ.ОК.0.9)
- Способность использовать основные законы естественно-научных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (КМ.ОК.0.10)
- Умение готовить презентации, научно-технические отчеты по результатам выполненной работы (КМ.П.ОП.0.1)
- Умение ставить задачу и разрабатывать алгоритм ее решения (КМ.П.ПР.1.2)
- Знание принципов применения методов математического анализа и моделирования при проектировании АСОИУ (КМ.П.НИ.1.16)
Предшествующий уровень образования обучаемого – среднее (полное) общее образование, среднее профессиональное образование.
Компетенции студента, формируемые в результате освоения учебной дисциплины, ожидаемые результаты образования и компетенции студента по завершении освоения программы учебной дисциплины
В результате освоения дисциплины студент должен:
Знать (КМ.ОК.0.1-2, КМ.ОК.0.9-10, КМ.П.ОП.0.1, КМ.П.ПР.1.2, КМ.П.НИ.1.16): основные действия над множествами, способы вычисления числа возможных комбинаций, способы представления логических (переключательных) функций, способы представления графов и методы оптимизации на графах, постановку и решение транспортных задач, анализ марковских цепей;
Уметь (КМ.ОК.0.1-2, КМ.ОК.0.9-10, КМ.П.ОП.0.1, КМ.П.ПР.1.2, КМ.П.НИ.1.16): применять действия над множествами, построить таблицу истинности логической функции, построить переключательную схему и упростить её, анализировать процессы с помощью графов, решать транспортную задачу, анализировать системы массового обслуживания;
Владеть (КМ.ОК.0.1-2, КМ.ОК.0.9-10, КМ.П.ОП.0.1, КМ.П.ПР.1.2, КМ.П.НИ.1.16): методами анализа действий над множествами, вычисления чисел комбинаций, навыками работы с логическими функциями, способами анализа графов.
Дисциплина включает следующие разделы:
- Теория множеств,
- Элементы комбинаторики,
- Основы математической логики,
- Графы,
- Оптимизация на взвешенных графах,
- Цепи Маркова (массовое обслуживание).
4 Структура и содержание учебной дисциплины
| Недели | Тема | Часов | Отчётность | |||
| Лекции | Практики | вид | выдана | сдана | ||
| Множества, действия над ними. | ТР №1 | 2 н. | 5 н. | |||
| Мощность множества. Элементы комбинаторики. | ||||||
| Бинарные отношения, функции. Виды бесконечных множеств. | ||||||
| Непрерывное и дискретное изменение величины. | ||||||
| Общее понятие логической функции. Основные логические функции | ТР №2 | 6 н. | 10 н. | |||
| СДНФ, СКНФ | ||||||
| Переключательные схемы и переключательные функции | ||||||
| Упрощение переключательных функций | ||||||
| Логика высказываний | ||||||
| Способы задания графов. | ТР №3 | 15 н. | 18 н. | |||
| Маршруты и циклы в графе. | ||||||
| Связность графа, его каркас. Дерево и лес. | ||||||
| Планарность графа. | ||||||
| Ориентированные, взвешенные графы, сети. | ||||||
| Оптимальный маршрут во взвешенном графе. | ||||||
| Транспортная задача. | АКР №1 | 18 н. | ||||
| Метод потенциалов. | ||||||
| Марковские цепи. | ||||||
| Зачётная работа | По расписанию сессии | |||||
| Итого: | 3 ТР, 1 АКР | Экзамен |
ТР №1 Множества, комбинаторика; ТР №2 Математическая логика;
ТР №3 Графы; АКР №1 Цепи Маркова.
Общая трудоёмкость дисциплины 6 ЗЕТ и 5,5 кредита.
5 СОДЕРЖАНИЕ КУРСА
Теория множеств (Л – 8 ч., Пр.– 4 ч.)
1 Способы задания множеств. Диаграммы Эйлера-Венна. Действия над множествами: сравнение, объединение, пересечение, , разность и симметрическая разность двух и более множеств. Универсальное множество и операция дополнения множества. Основные свойства перечисленных действий.
2 Мощность конечного множества, мощность объединения нескольких множеств (формула включения-исключения).
3 Элементы комбинаторики: Прямое (декартово) произведение множеств и число простых комбинаций (векторов); Числа перестановок, размещений и сочетаний. Треугольник Паскаля, бином Ньютона. Их связь с числом подмножеств.
4 Соответствия на множествах, их виды. Понятие функции. Взаимооднозначные соответствия, их связь с мощностью множеств.
5 Понятие счётного множества. Счётность множества целых и рациональных чисел. Теорема Кантора. Континуальные множества.
6 Непрерывное и дискретное изменение переменной величины. Процесс дискретизации непрерывной переменной, переход от аналогово (непрерывного) сигнала к цифровому (дискретному).
Математическая логика (Л – 10 ч., Пр.– 4 ч.)
7 Определение логических функций нескольких переменных. Число всевозможных наборов логических переменных и логических функций от n переменных. Правило составления таблицы истинности логической функции.
8 Все логические функции одной переменной (одноместные логические операции). Определения и таблицы истинности основных логических функций от двух переменных (бинарных логических операций): конъюнкции, дизъюнкции, строгой дизъюнкции, импликации, эквиваленции.
9 Перечисление всех логических функций двух переменных в виде сводной таблицы с указанием названий каждой из них.
10 Проверка совпадения двух логических функций с одинаковым числом переменных по их таблицам истинности. Понятие тавтологии (тождественно-истинной функции, константы). Основные логические тождества.
11 Дизъюнктивная нормальная форма (ДНФ) и СДНФ. Единственность СДНФ. Получение СДНФ по таблице истинности логической функции. Получение из ДНФ соответствующей СДНФ.
12 Конъюнктивная нормальная форма (КНФ) и СКНФ. Единственность СДНФ. Получение СКНФ по таблице истинности логической функции. Получение из КНФ соответствующей СКНФ.
13 Переключательная схема и реализуемая ей переключательная функция. Изображение с помощью двоичного куба. Построение переключательной схемы по переключательной функции.
14 Минимизация логической (переключательной) функции с помощью тождеств; на двоичном кубе; метод склейки.
15 Графическое представление логической (переключательной) функции как зависимости выходного сигнала от входных с помощью стандартных элементов.
16 Запись высказывания в виде логической функции (формулы) и его проверка на логичность, непротиворечивость (является ли высказывание тавтологией).
17 Теорема как высказывание, её посыл (условия) и заключение (вывод). Случаи верных и неверных теорем. Прямая, обратная и противоположная теоремы. Необходимое условие и достаточное условие в виде теорем, случаи выполнения и нарушения необходимого и (или, либо) достаточного условий.
18 Замкнутый класс логических функций. Полная система функций. Теорема (Поста) о полноте системы логических функций. Классы сохраняющих константы 0 и 1, монотонных, самодвойственных, линейных функций. Примеры полных систем логических функций.
Графы (Л – 12 ч., Пр.– 6 ч.)
36. Общие понятия: граф, множество его вершин и дуг; смежность вершин и задание графа матрицей (списком) смежностей; инцидентность дугам графа его вершин, матрица (список) инцидентностей; Ребра в неориентированном графе и способ представления ориентированного графа неориентированным, вид матрицы смежностей при этом; Задание графа бинарным отношением на некотором множестве.
37. Эквивалентность двух графов, способ проверки эквивалентности графов при их задании матрицами смежностей. Критерий неэквивалентности графов.
38. Понятия маршрута в графе, достижимости одной вершины из другой, цикла, простого маршрута. Связность (односвязность) графа, его многосвязность.
39. Эйлеров цикл в односвязном графе. Теорема Эйлера о наличии эйлерова цикла или маршрута в графе. Задача о кенигсбергских мостах, о возможности изобразить фигуру без отрыва и прохождения дважды, задача о пересечении всех рёбер графа непрерывной линией.
40. Задача о трёх колодцах и трёх домах. Понятие планарного графа. Планарный граф как изображение многогранника на плоскости. Теорема Эйлера о многогранниках (о планарности графа). Теорема о непланарности графа. Укладка планарного графа на сфере и непланарного 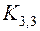 на торе.
на торе.
41. Взвешенные графы, их применение для описания сложных процессов. Алгоритм отыскания маршрута с наименьшим общим весом и критического маршрута в сети. Анализ общего времени выполнения сложного процесса и возможность его уменьшения.
42. Применение графов при анализе систем, которые могут находится в нескольких состояниях. Анализ задачи о Ханойской башне.
Транспортная задача (Л – 4 ч., Пр.– 2 ч.)
43. Стандартный вид транспортной задачи, изображение в виде графа или таблицей. Условие разрешимости транспортной задачи. Введение дополнительных пунктов назначения или отправления. Нахождение опорного решения (плана) методами северо-западного угла и наименьшего элемента.
44. Метод потенциалов проверки опорного решения на оптимальность. Сдвиг по циклу в опорном решении.
45. Дополнительные условия в транспортной задаче: запрет пути, перевозка заданного, не менее либо не более заданного количества.
Марковские цепи (Л – 2 ч., Пр.– 2 ч.)
46. Понятие марковской цепи, возможные состояния системы и матрица вероятностей перехода за один шаг (при дискретном изменении времени). Стационарное распределение и предельные вероятности состояний системы, правило их нахождения.
47. Однородные марковские цепи с непрерывным изменением времени, матрица интенсивности переходов. Нахождение предельных вероятностей по системе Колмогорова.
48. Многоканальная система массового обслуживания с известными интенсивностями заявок и их обслуживания. Анализ вероятности отказа для заявки и среднего числа занятых каналов.
Примеры задач:
ТР №1 (Множества и комбинаторика)
1) Для множеств А={а, в, с, {d, e}, f}, B={ {a, g}, b, c, h}
найти
а) |A|, |B|;
б) 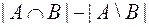 ;
;
в) Мощность для АхВ и указать несколько его элементов;
г) Число всевозможных перестановок всех элементов А и указать несколько таких перестановок;
д) Число всевозможных подмножеств для В и указать несколько подмножеств различной мощности;
2) Определить число возможных числовых пар без повторений, каждое из чисел является натуральным числом от 7 до 20 чётным и не кратным пяти.
3) Вычислить 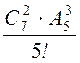 ;
;
ТР №2 (Логика)
1) Составить таблицу истинности логической функции 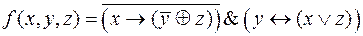 , по ней записать функцию в виде ДНФ и КНФ, построив переключательную схему и минимизировать её;
, по ней записать функцию в виде ДНФ и КНФ, построив переключательную схему и минимизировать её;
2) Требуется соединить четыре выключателя в схему так, что лампа загорится в случаях, когда включен первый и выключен второй или в случае включения большинства из выключателей с номерами 2, 3, 4. Для такой схемы составить переключательную функцию, записать её СДНФ и СКНФ, затем минимизировать и изобразить полученную схему;
3) Проверить логичность следующего вывода:
«Если на улице дождя нет, то я не беру зонт. Если я взял зонт, то надеваю и плащ. Сегодня я плаща не одел. Следовательно, сегодня дождя не было».
ТР №3
1) Изобразить граф, заданный своей матрицей смежности А, составить его матрицу инцидентности, составить матрицу достижимости из каждой вершины и проверить связность графа. Изобразить рядом эквивалентный ему граф.
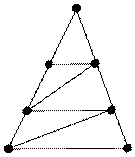
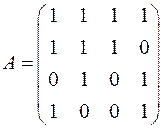
2) Возможно ли соединить семь точек как на рисунке
непрерывной линией без её наложений
и прохождения по участкам дважды?
3) 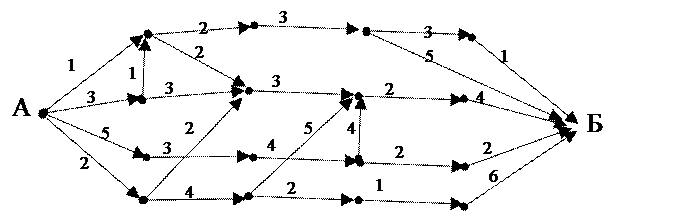 Во взвешенном графе найти маршрут из А в Б с наименьшей суммой весов и критический маршрут (с наибольшей суммой весов).
Во взвешенном графе найти маршрут из А в Б с наименьшей суммой весов и критический маршрут (с наибольшей суммой весов).
АКР №1
Телефонная станция имеет 5 каналов связи с интенсивностью 7 звонков за 10 минут. Среднее время обслуживания звонка 3,4 минуты. Найти вероятности каждого возможного количества звонков на станцию и вероятность отказа. Рентабельна ли работа станции, если содержание канала связи в месяц обходится в 10 000 у.е., а обработанный звонок в среднем приносит 1,5 у.е.?
| <== предыдущая страница | | | следующая страница ==> |
| Тема 2.2 Оборотный капитал | | | КРИТЕРИЙ ИТОГОВОЙ ОЦЕНКИ |
Дата добавления: 2014-11-04; просмотров: 587; Нарушение авторских прав

Мы поможем в написании ваших работ!