Улугбек (1394-1449), правитель и учёный

3. В XIII в. Среднюю Азию, Иран, Сирию, Месопотамию завоевали монголы. Крупнейший математик этого времени Насир-эд-дин ат-Туси (1201-1274) – уроженец г. Туса в Хорасане. В 50-х гг. XIII в. он работал в Кухистане (северо-восток Ирана), в столице государства, управлявшегося террористической сектой ассасинов (убийц), которые воевали с множеством врагов. Их врагами были как багдадские халифы, так и европейские крестоносцы, но, в конце концов, в 1253 г. их столицу завоевали монголы. После этого ат-Туси перешёл на службу к монгольскому хану Хулагу, внуку Чингисхана. По совету Туси Хулагу-хан организовал в своей столице Мараге (южный Азербайджан) астрономическую обсерваторию, куда привлекали для работы учёных из всех стран, захваченных к этому времени монголами. Таким образом и возникла так называемая Марагинская школа.

Насир-эд-дин ат-Туси перевёл с греческого на арабский язык и снабдил комментариями и добавлениями важнейшие математические, астрономические, физические труды древних авторов: «Начала», «Феномены» и «Оптику» Евклида, «Об измерении круга» и «О шаре и цилиндре» Архимеда, «Альмагест» Птолемея, «Конические сечения» Аполлония и «Сферику» Феодосия. Он составил комментарии к книге «Шмарат» («Обозначения») Ибн Сины (Авиценны). Из его собственных трудов назовём книги «Шакл-ул-Кита», посвящённую сферической тригонометрии и теории отношений, «Каванд-ул-Хандаса» (трактат по геометрии) и «Таэкира» (трактат по астрономии).

Ещё в юности на Насир-эд-дина ат-Туси большое впечатление произвел геометрический труд Омара Хайяма «Комментарий к трудностям во введениях книги Евклида». До наших дней сохранились две редакции «Тахрир Уклидас» – перевода «начал» Евклида с комментариями и добавлениями Насир-эд-дина. Учёный предпринял очередную попытку доказать пятый постулат Евклида. Первая из двух упомянутых редакций, содержащая 13 книг, была напечатана в Риме в 1594 г. на арабском языке. Вторая содержит 15 книг (две добавлены комментаторами «Начал»). Она была издана также в Риме в 1657 г. в переводе на латынь. С этими изданиями были знакомы английский математик Джон Валлис (1616-1703 гг.) и итальянский учёный Джованни Саккери (1667-1733 гг.), труды которых, в свою очередь, сыграли важную роль в предыстории неевклидовой геометрии.

Вопросы к семинару «Математика на средневековом востоке»

1. Изложите вкратце историю возникновения ислама и Арабского халифата, а также постепенного распада этого государства.

2. Что Вы можете рассказать о развитии науки в средневековых арабоязычных государствах?

3. Расскажите о научной деятельности ал-Хорезми и значении его арифметического и алгебраического трактатов для развития математической науки.

4. Расскажите о наиболее значительных учёных стран арабоязычного Востока в X – XV веках.

5. Расскажите о роли математиков арабоязычного Востока в предыстории создания неевклидовой геометрии.

Рекомендуемые темы для рефератов и сообщений.

1. «Арифметический трактат» ал-Хорезми.

2. «Алгебраический трактат» ал-Хорезми.

3. Геометрия в трудах ал-Хорезми.

4. Омар Хайям – поэт и учёный.

Литература по теме.

1. Сираждинов С.Х., Матвиевская Г.П. Ал – Хорезми – выдающийся математик и астроном средневековья: пособие для учащихся. – М.: Просвещение, 1983. – 78 с.

2. Юшкевич А.П. Омар Хайям и его «Алгебра»./ Труды Института истории естествознания, 1948, 2.

3. Омар Хайям. Трактаты. Перевод Б.А.Розенфельда. Вступительная статья и комментарии Б.А.Розенфельда и А.П.Юшкевича. – М.: Изд. Восточной литературы, 1961. – 338 с.

4. Розенфельд Б.А., Рожанская М.М., Соколовская З.К. Абу-р-Райхан ал-Бируни. – М.: Наука, 1973. – 271 с.

5. Сираждинов С.Х., Матвиевская Г.П. Абу Райхан Беруни и его математические труды: пособие для учащихся. – М.: Просвещение, 1978. – 95 с.

Улугбек (1394-1449), правитель и учёный

План.

1. Жизнь султана Улугбека.

2. Сподвижники Улугбека.

3. Некоторые астрономические инструменты средневекового Востока.

4. Изучение эпохи Улугбека

а) Раскопки обсерватории Улугбека в 1908-1909 гг.

б) Раскопки захоронения тимуридов в 1941-1946 гг.

5. Основные достижения математиков мусульманского мира в VIII-XV вв.

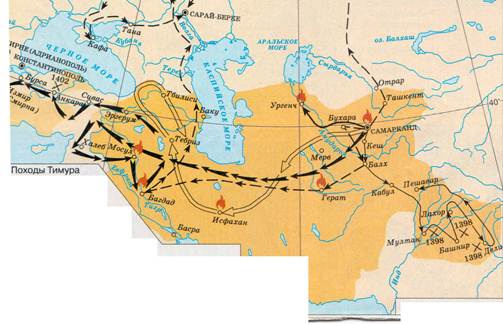
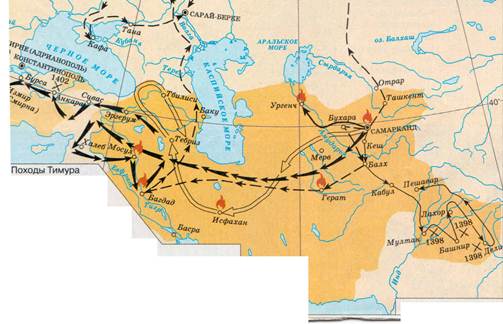
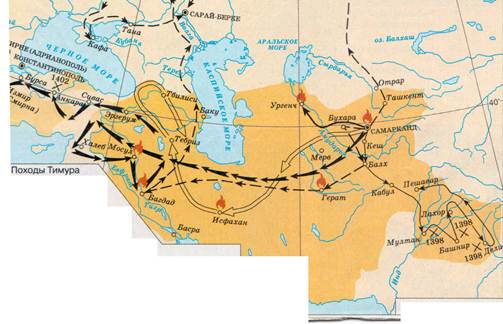
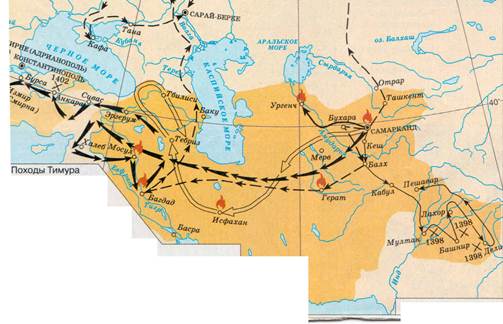
Рисунок . Держава Тимура.

В XV в. в Самарканде возникла математическая и астрономическая школа Улугбека (1394-1449), которая занимает особенно видное место в истории науки средневекового Востока.

Улугбек был внуком знаменитого завоевателя Тимура (Тамерлана) (1336-1405). Отцом Улугбека был третий сын Тимура Шахрух (1377-1447). Согласно легенде, получив известие о рождении этого внука, Тамерлан, захвативший накануне крепость Мардин, по случаю великой радости даровал жизнь всему её населению. Ребёнку дали имя Мухаммед Тарагай, но ещё в юности его стали называть Улугбек, что означает «Великий князь». Воспитание наследников при дворе Тимура считалось делом государственной важности. Мальчиков воспитывали не матери, а специально назначенные люди. Улугбек был передан на воспитание старшей жене Тимура Сарай-Мульк Ханым, которая растила его до 11 лет. Затем его наставником стал образованнейший и талантливый человек Хамза ибн Али Малик Туси (шейх Ариф Азари), имевший большое влияние на своего воспитанника.

В 1405 г. Тимур умер во время одного из своих походов. В течение четырёх лет после его смерти между наследниками шла междоусобная борьба за власть. В результате образовалось два государства – Хорасанское с центром в Герате и во главе с отцом Улугбека Шахрухом и Мавераннахрское с центром в Самарканде и во главе с самим Улугбеком, которому было в это время всего 15 лет.

До смерти Шахруха в 1447 г. империя Тимура сохранялась от распада, пресекались как притязания соседей, так и попытки междоусобиц между родственниками. Но когда Шахрух умер, вновь возник вопрос о престолонаследии. Улугбек к этому времени был единственным оставшимся в живых сыном своего отца, но уже были взрослыми его сыновья и племянники, каждому из которых хотелось взять как можно большую власть. Сам Улугбек при этом в принципе поддерживал своего старшего сына Абу-ал-Латифа, но он считал, что Самарканд должен играть главенствующую роль в государстве.

В ходе разгоревшейся междоусобицы, участники которой воевали каждый против каждого, то объединяясь, то предавая друг друга, возникло противостояние и между Улугбеком и его старшим сыном. В конце концов сын полностью разбил войска отца, втайне устроил суд над ним, и фактически приговорил его к смерти. Улугбек, отправившийся в паломничество в Мекку, был убит, едва успев немного отъехать от Самарканда.

Через несколько дней Абу-ал-Латиф казнил и своего младшего брата, которому отец, по его мнению, оказывал предпочтение. Но сам он пробыл у власти недолго. Своей жестокостью он менее чем через год вызвал возмущение в войсках и народе и был свергнут.

Во время также очень короткого правления племянника Улугбека Абдуллы (1450-1451), которого возвели на престол заговорщики, свергшие Абу-ал-Латифа, останки Улугбека были перезахоронены в великолепной царской усыпальнице Гур-Эмир в Самарканде. Этот мавзолей начали строить по приказу Тимура в 1403 г., когда умер его любимый внук и наследник Мухаммед Султан. Через два года там был захоронен сам Тимур, а в 1449 г. – его сын Шахрух, отец Улугбека.

Как образованный правитель, понимавший значение наук в жизни общества, Улугбек содействовал развитию просвещения в своём государстве. Об этом, в частности, свидетельствуют сохранившиеся до наших дней великолепные здания высших духовных школ – медресе, построенных им в Бухаре (1417г.), Самарканде (1417-1420 гг.) и Гиждуване (1433г.).

Рисунок . Самарканд. Мавзолей Гур-Эмир.

Медресе Улугбека в Самарканде функционировало до XIX в. В наши дни оно является частью архитектурного ансамбля площади Регистан, на которой, кроме него, располагаются медресе Шер-Дор (1619-1636 гг.) и Тилля-Кари (1647-1660 гг.). При Улугбеке это медресе было центром, объединявшим учёных, съезжавшихся в Самарканд по приглашению Улугбека. Примерно в одно время с ним начала строиться и Самаркандская обсерватория.

Рисунок .Самарканд. Площадь Регистан.

Рисунок .Самарканд. Медресе Улугбека.

Назовём нескольких учёных Самаркандской научной школы – сподвижников Улугбека.

Кази-заде ар-Руми (ок. 1360-ок.1437 гг.) был родом из города Рум в Турции. Он был приглашён Улугбеком в Самарканд. О том, каким уважением он пользовался там, говорит хотя бы то, что похоронен этот учёный в некрополе самой высокой знати Шахи-Зинда, и его мавзолей самый высокий и красивый на этом кладбище.

Рисунок . Самарканд. Шахи-Зинда.

Рисунок . Мавзолей Кази-Заде ар-Руми.

Гийас-ад-Дин Джамшид аль-Каши (3-я четверть XIV в.; ум. ок. 1430 г.)Приехал в Самарканд по приглашению Улугбека в 1416-17 г. С именем этого ученого связывается два важных открытия. Первое из них – десятичные дроби. Напомним, что ал-Хорезми изложил арифметику целых чисел в десятичной позиционной системе. Но, несмотря на это, дроби математики Востока использовали шестидесятеричные, которыми пользовался ещё Птолемей. Астрономы Самаркандской обсерватории, благодаря аль-Каши, начинают широко использовать в своей работе десятичные дроби, которые, конечно, существенно удобнее при проведении расчётов.

Вспомним также, что с именем ал-Хорезми связывается выделение алгебры в самостоятельную науку о решении уравнений. Но алгебра ал-Хорезми ограничивается уравнениями первой и второй степеней. Математики последующих поколений начинают интересоваться и уравнениями третьей степени, к которым приводят разнообразные задачи, например:

· Одна из задач Архимеда – о рассечении шара плоскостью на два сегмента с заданным отношением объёмов.

· Задача о трисекции угла. Именно математики стран ислама свели её к уравнению , где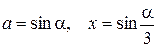

· Отыскание стороны правильного 9-угольника или 7-угольника.

В методах решения кубических уравнений отразилось многообразие различных средств, характерное для математики Востока. Были попытки численного решения, использовался метод Менехма, т.е. решение с помощью пересечения конических сечений. Омар Хайям решал кубические уравнения геометрическим способом. Джамшид аль-Каши – автор первого итерационного метода приближённого решения кубического уравнения. Основной труд аль-Каши называется «Ключ арифметики». Он написан в 1427 г.

Ала-ад Дин Али ал-Кушчи (ок. 1402-1474),в отличие от двух вышеупомянутых учёных, был уроженцем Самарканда и принадлежал к придворным Улугбека. «Кушчи» означает «сын сокольничего». Ему пришлось пережить гибель Улугбека и распад его школы. Последние годы жизни Али Кушчи провёл в Турции.

Мирим Челеби (ок. 1435-1525 гг.) –внук ал-Кушчи по материнской линии и Кази-заде ар-Руми по отцовской. Вместе с ал-Кушчи он покинул родину после смерти Улугбека и работал в Турции, а затем – в различных городах Малой Азии.

Основной труд Самаркандской научной школы сохранился до наших дней в большом количестве рукописных копий, где он фигурирует под разными названиями. Наиболее распространённое из них – Зидж Улугбека.

Рисунок . Зидж Улугбека.

Зиджаминазываются сочинения, составляющие значительную часть средневековой восточной астрономической литературы. Они представляют собой сборники астрологических и тригонометрических таблиц, необходимых для решения задач практической астрономии. Это различные измерения времени, отыскание географических координат места, определение положения светила на небесной сфере, определение моментов их восхода и захода и т.д. В зиджах давались правила пользования таблицами и часто – более или менее развёрнутые теоретические обоснования этих правил.

Первые арабские зиджи относятся к VIII-IX вв. На них оказали влияние аналогичные индийские сочинения и «Альмагест» Птолемея. Зидж Улугбека и комментарии к нему приобрёл большую популярность в странах Востока, среди учёных Индии, а в XVII в. – и в Европе.

Говоря о точности астрономических таблиц, составленных восточными учёными, мы должны были задуматься над тем, какие инструменты использовали эти учёные в своей работе.

Астрономические инструменты дотелескопического периода были угломерными. Некоторое представление о таких инструментах мы получим, если рассмотрим поближе самый распространённый из них − астролябию.

Рисунок .Астролябия работы Мухаммед-Земана Ибн Ходжа Шарифуддина Хасана. XVII в. Музей истории Узбекистана.

Астролябия состоит из неподвижной части, которая называется тимпан,и подвижной − паукаилирешётки.Подвижной является и расположенная сверху планка −алидадас двумя отверстиями − диоптрамии остриями, указывающими величину угла.К пластинке сверху, называемой троном,крепится подвес и кольцо, за которое можно держать астролябию, или подвесить её, например, к седлу.

Лицевая сторона тимпана обычно бывает окружена линией, называемой лимбом, и разделённой на 360 градусов. Внутри лимба перемещается паук, это диск с отверстиями. На нём, в свою очередь, имеется круг, на котором написаны названия двенадцати знаков зодиака. Этот круг называется эклиптикой.На эклиптике находятся фигуры, похожие на треугольники, на которых написаны названия неподвижных звёзд. Это так называемые указатели

звёзд.

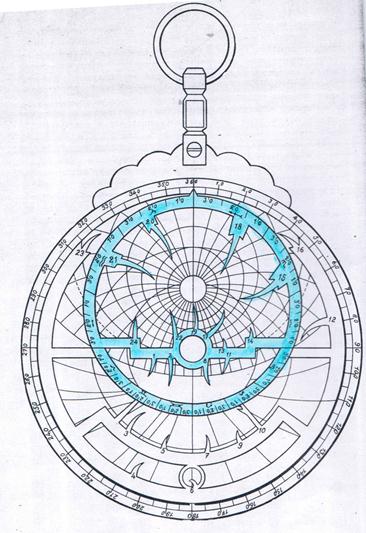
Рисунок . Тимпан и паук. Цифры на остриях относятся к неподвижным звёздам.

Тимпаны изготавливались специально, для каждой местности − свой.

Рисунок 4. Работа с астролябией.

Астролябия в странах ислама была одним из самых необходимых предметов. Этим инструментом пользовались далеко не только учёные, поэтому существовали различные астролябии, как простой конструкции, так и весьма сложные, для работы с которыми писались специальные руководства. В средневековой научной литературе немало трактатов о работе с астролябией. Выше упоминался, например, «Трактат об астролябии» Ал-Хорезми. У Бируни также есть труд «Астролябии». В его «Науке звёзд» также есть раздел, посвящённый работе с астролябией.

Рисунок . Работа с астролябией.

Угломерными были и другие астрономические инструменты, которыми пользовались в средние века в обсерваториях стран ислама, а затем и в Европе. Один из первых таких инструментов был построен в конце Х века в г. Рее Абу Махмудом Худжанди (из Ходжента) и назван в честь буидского правителя Рея Фахр-ад-Даулы Фахриев секстант. Этот инструмент был подробно описан аль-Бируни, который жил и работал в Рее в 990-х годах. Секстантом инструмент называется потому, что основной его частью является дуга, составляющая шестую часть круга. Существовали также октанты и квадранты. Главным инструментом обсерватории Улугбека был, скорее всего, огромный квадрант. Фрагмент его сохранился до наших дней.

Обсерватория Улугбека была построена в Самарканде около 1420 года и разрушена сыном Улугбека Абу ал-Латифом, который сверг и погубил своего отца в 1449 году. Внешний облик обсерватории описан в исторических документах самыми общими словами, из которых можно понять, что это было красивое круглое трёхэтажное здание. Европейские учёные последующих столетий ставили эту обсерваторию в ряд самых знаменитых обсерваторий

Рисунок . Фрагмент квадранта Улугбека.

средневекового Востока, отмечая точность астрономических наблюдений, описанных в «Зидже» Улугбека.

Из разрозненных фактов, приводившихся в описаниях восточных авторов, можно было заключить, что обсерватория находилась на окраине Самарканда, но к XIX веку возникли и другие версии. Всё, что оставалось от обсерватории, к тому времени в полном смысле слова сравнялось с землёй. Целенаправленные поиски остатков обсерватории Улугбека начались в самом конце XIX века и связаны с именем В.Л.Вяткина.

Василий Лаврентьевич Вяткин (1869-1932)− один из замечательных русских энтузиастов-исследователей истории культуры Средней Азии. В 1894 году он закончил учительскую семинарию в Ташкенте, а затем много лет работал при областном правлении в Самарканде. По документам ему удалось установить местонахождение обсерватории Улугбека, и в 1908 году по инициативе Вяткина на указанном им месте были начаты раскопки. В первый же сезон раскопок были обнаружены фрагменты главного инструмента обсерватории. Вяткин сразу предположил, что это был квадрант. Позднее возникали и другие версии, но, в конце концов, гипотеза Вяткина подтвердилась.

Сохранившаяся часть инструмента Улугбека представляет собой уходящую глубоко под землю траншею, в которой расположены две параллельные дуги, снизу выложенные кирпичом, а сверху облицованные мрамором. Расстояние между дугами на уровне мраморных плит равно 2,33 м. Между дугами и по обе стороны от них располагаются ступени, по которым поднимался наблюдатель. По всей вероятности, дуги с лестницей поднимались и над землёй. На вершине башни находился диоптр, через который наблюдатель должен был увидеть интересующее его небесное светило. А на мраморной облицовке и до наших дней сохранились фрагменты градуировки, плиты с обозначениями градусных делений. Плита с делениями 19° и 21° была найдена не сразу. Её обнаружение и подтвердило, что инструмент являлся квадрантом.

Рисунок 58.

В связи с началом первой мировой войны и событий, последовавших после неё, изучение истории школы Улугбека приостановилось и возобновилось только в 40-х годах ХХ века.

В 1941 г. в связи с 500-летним юбилеем великого восточного поэта Алишера Навои (1441-1501) в Советском союзе решено было активизировать изучение эпохи Навои, которую, конечно, можно назвать и эпохой Улугбека. В связи с этим летом 1941 года была организована экспедиция для изучения погребений Тимуридов в мавзолее Гур-Эмир. В экспедиции участвовал известнейший советский археолог и скульптор Михаил Михайлович Герасимов (1908-1970), автор уникальной методики восстановления лица человека по сохранившимся лицевым костям черепа. Вам, вероятно, известно, что именно Герасимов воссоздал, например, внешний облик Иоанна Грозного и его сыновей, захороненных в царской усыпальнице Московского кремля. Метод Герасимова находит широкое применение как в археологии и искусстве скульптуры, так и в криминалистике. Нередко учёным разных специальностей приходится помогать друг другу в работе. Несколько лет назад, например, доктор медицинских наук из Оренбурга, профессор В.К. Филиппов, специалист в области судебной медицины, владеющий методом Герасимова, участвовал в работе по восстановлению внешнего облика Ивана Сусанина, который, как известно, был зарублен поляками.

В 1941 году Герасимов намеревался создать портреты Тимура и его потомков. В то же время в экспедиции участвовали архитекторы и астрономы, которые должны были продолжить работу по изучению научной деятельности Улугбека. Раскопки начались буквально накануне начала Великой Отечественной войны. Экспедицию пришлось на некоторое время прервать, однако она не прекратила свою работу. М.М.Герасимов все военные годы трудился в Узбекистане. Время от времени он выезжал в Самарканд, а в остальное время жил и работал в Ташкенте на территории Института астрономии Академии Наук Узбекистана, которым руководил Владимир Петрович Щеглов (1904-1985).В специально оборудованной здесь мастерской Герасимов и создал портреты Тимура и его потомков. Авторская копия портрета Улугбека была впоследствии подарена музею Института астрономии.

Рисунок .Портрет Улугбека работы М.М.Герасимова. Этот портрет создан через пять столетий после смерти человека, и, тем не менее, он подлинный!

В годы войны и после неё продолжалась и работа других учёных, изучавших эпоху Улугбека. В 1953 г. на месте его обсерватории был открыт музей, имеющий богатую коллекцию и замечательное художественное оформление. В этом музее представлены реконструкции обсерватории, предлагавшиеся историками, архитекторами и астрономами в течение многих лет.

Здесь находится и макет обсерватории.

−

Рисунок . Макет обсерватории Улугбека. Автор - доктор архитектуры В.А.Нильсен.

Академик Академии наук Узбекистана В.П.Щеглов более 30-ти лет руководил Институтом астрономии в Ташкенте и создал там поистине уникальный музей астрономических инструментов.

Один из экспонатов его музея − точная копия небесного глобуса Улугбека, который сохранил и увёз из Самарканда после гибели обсерватории Али Кушчи. Теперь этот глобус находится в Англии, в частной коллекции. Копию выполнил мастер − энтузиаст по средневековым описаниям и современной фотографии, найденной в иллюстрированном журнале.

Рисунок . В.П.Щеглов (1904-1985)

Первые небесные глобусы на Востоке появились во второй половине ХIII в. Сохранился, например, глобус из Марагинской обсерватории, изготовленный в 1279 году под руководством Нсирэддина ат-Туси. В середине XIV века такие глобусы появляются и в Европе (первые − в Германии).Датский астроном XVI века Тихо Браге (1546-1601)описал небесный глобус, изготовленный в1584 году, которым он, вероятно, пользовался.В 1576 г на острове Вен близ Копенгагена датский король построил для Тихо Брагеобсерваторию,которую ученый назвал Ураниборг, т. дворец Урании, музы астрономии. Здесь изготавливались инструменты, с помощью которых измерялось положение светил на небесной сфере. Тихо Браге составил каталог примерно 800 звёзд. Среди инструментов был и 6-метровый стенной квадрант. Таким образом, европейские астрономы XVI века уже активно пользовались

инструментами, аналогичными инструментам, распространённым на Востоке двумя столетиями ранее.

Рисунок . Тихо Браге в обсерватории «Ураниборг». Худ. Н Маркова.

В XVII столетии уже появились первые телескопы. Но польский астроном, механик, оптик и художник Ян Гевелий (1611-1687)предпочитал проводить астрономические наблюдения ещё с помощью угломерных инструментов, и был известен точностью своих расчетов. Известно, что он и Э. Галлей устроили однажды соревнование. Галлей делал телескопические наблюдения, а Гевелий - глазомерные оценки, и результаты получились одинаковые. Гевелий создал обсерваторию в Гданьске и инструменты для неё конструировал сам. Им составлен каталог координат 1564 звёзд, более точный, чем каталог Тихо Браге.

Рисунок . Ян Гевелий и его жена Эльжбета ведут наблюдения звёздного неба с помощью секстанта. Худ. Н Маркова.

Одним из самых известных его трудов является атлас «Описание всего звёздного неба», который Гевелий, замечательный художник, снабдил собственными рисунками. Одно из открытых им созвездий называется секстантом в честь любимого инструмента Гевелия. В астрономических наблюдениях ему помогает его жена Эльжбета, одна из первых женщин− учёных нового времени, самостоятельно занимавшаяся обработкой результатов наблюдений и завершившая издание трудов мужа после его смерти. Кстати, младшая сестра Тихо Браге София также успешно занималась астрономией.

Атлас Гевелия в 70-е годы ХХ века был несколько раз переиздан в Ташкенте под руководством уже упоминавшегося В.П.Щеглова. В написанной им вступительной статье к этому изданию рассказывается о роли школы Улугбека в последующем развитии астрономической науки и о той оценке, которую давали европейские учёные XVII столетия деятельности этой школы.

5. заканчивая раздел курса, посвящённый математике стран ислама, перечислим основные достижения математиков мусульманского мира в VIII-XV вв.

В области арифметики и комбинаторики:

o Усовершенствование позиционной шестидесятеричной системы счисления.

o Широкое использование индийской десятичной позиционной системы счисления с нулём (Аль-Хорезми, IX в.). Введение десятичных дробей (XV в.). Это чрезвычайно расширило возможности для вычислительной работы, для составления астрономических таблиц. Заметим, что Птолемей пользовался ещё шестидесятеричными дробями, что сильно усложняло вычисления. С появлением десятичных дробей открылась возможность проводить сложнейшие расчёты на бумаге или на специальной доске, покрытой пылью. Именно потому на Востоке математика быстро приобрела вычислительный характер. Успехи в развитии вычислительных методов привели к составлению исключительно точных астрономических таблиц. Они также привели к тому, что в XI веке начали появляться приближённые методы решения математических задач.

o Разработка приёмов извлечения корней из чисел.

o Первое применение (в словесном виде) формулы, названной много позже формулой бинома Ньютона для любого натурального показателя.

o Расширение понятия о числе. Выработка понятия действительного положительного числа.

В области алгебры.

o Выделение алгебры в особую математическую дисциплину (Аль-Хорезми, Аль-Мисри, Омар Хайям).

o Применение числовой алгебры в измерительной геометрии и тригонометрии. Например, сведение задачи о трисекции угла к решению кубического уравнения.

o Появление итерационного метода численного решения уравнения третьей степени (Аль-Каши).

В области геометрии и тригонометрии.

o Создание плоской и сферической тригонометрии. Построение чрезвычайно точных и полных тригонометрических таблиц. Основой для формирования тригонометрии послужили, во-первых, результаты Птолемея и Менелая, их исчисление хорд и соответствующие таблицы. Во-вторых, операции с линиями синуса и косинуса у древних индийцев, в-третьих, собственный опыт восточных учёных в астрономических наблюдениях. В математике средневекового Востока тригонометрия приобрела положение отдельной математической дисциплины, преобразовавшись из совокупности вспомогательных средств астрономии в науку о соотношениях в плоских и сферических треугольниках, о способах решения этих треугольников. В этой науке преобладающую роль стали играть алгоритмически-вычислительные средства, но не было ещё привычной для нас символики. Дальнейшее развитие тригонометрии начинается в Европе со второй половины XVI века.

o Исследования по теории параллельных (Омар Хайям, ат-Туси).

Дата добавления: 2014-05-17; просмотров: 1230; Нарушение авторских прав

Мы поможем в написании ваших работ!