Дисперсионное пространство и геометрия дифракции

Рассмотрим сначала одноволновой случай. Опишем вокруг начала координат ОР сферу радиусом (см. 1.9). Эта сфера является геометрическим местом начал векторов ( ), характеризующих распространение одноволнового поля. Каждой точке А_i этой сферы отвечает поле с волновым вектором (рис. 2а). То, что эта поверхность-сфера, демонстрирует то, что коэффициент преломления одноволнового поля не зависит от направления распространения и поляризации волны.

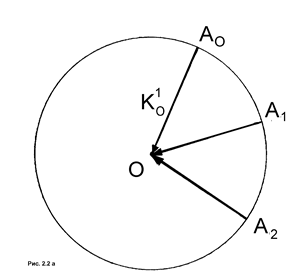
Рисунок 2а - Одноволновое поле (сечение сферы проходящее через т.О)

Поверхность, на которой расположены начала векторов в двухволновом случае – дисперсионная поверхность, может быть построена следующим образом. Опишем сферы радиусом

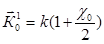вокруг узлов О и Н ОР (узел 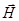отвечает вектору ОР отражающей системы плоскостей) (рис. 1.2б). Пока точки А_i начала векторов 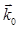лежат на сфере 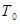, поле состоит из одной волны. Однако при приближении точки А к точке E появляется отраженная волна. Интерференция волн и 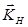изменяет коэффициент преломления и геометрическое место точек начал векторов и 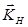образует иную, чем в одноволновом случае поверхность. Поскольку каждой точке поверхности отвечает своя пара векторов и 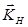, свой коэффициент преломления и соответственно, определенное волновое поле, эти точки называют точками возбуждения волнового поля, а поверхность – геометрическое место точек возбуждения всех разрешенных волновых полей – дисперсионной поверхностью.

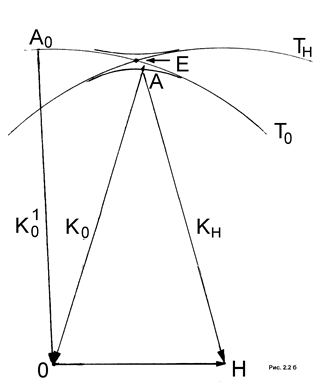
Рисунок 2б - Двухлучевое поле (сечение соответствующее плоскости дифракции)

Чтобы представить форму дисперсионной поверхности, учитывая малое изменение длины волновых векторов из-за преломления, можно рассматривать положение точек возбуждения вблизи точки E. Поэтому заменим окружност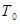и и 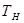касательными к ним в точке Е. В качестве осей координат выберем нормали к 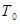и 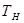. Вещественные координаты точки А, характеризующие изменения ( ) из-за преломления или перехода от одно- к двухволновому полю, запишем в виде

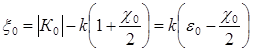(1.13)

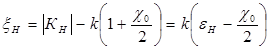
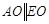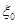Здесь учтено, что в ближайшей окрестности точки E можно полагать, что , а , т.е. оси и 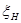практически параллельны и 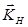. Теперь равенство (2-11) перепишется в виде:

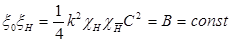(1.14)

В заданной косоугольной системе координат 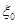и 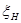задают координаты точек возбуждения разрешенных волновых полей, отвечающие значениям преломления, вычисляемым по уравнению (1.11). Разным направлениям первичной волны изменяющимся вблизи отражающего положения, отвечают разные точки возбуждения. Уравнение (1.14) описывает сечения дисперсионной поверхности лучевой плоскостью, плоскостью дифракции.

Каждое сечение для заданной поляризации является, гиперболой, две ветви которой отвечают положительным и отрицательным значениям 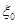и 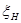. Ветвь, отвечающая положительным 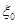и 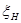, отвечает полям второго типа, отрицательным – первого.

Итак, совокупность точек возбуждения лежащих на дисперсионной поверхности определяет все волновые поля, состоящие из двух волн, образующихся, когда в отражающем положении находится одна система атомных плоскостей.

Положение точки возбуждения определяет все свойства волнового поля. Действительно, уравнения (2-12) позволяют получить отношение амплитуд волн, составляющих поля. Если в соответствии с законом центросимметричности отражения

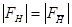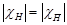то и

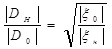(1.15)

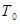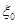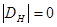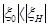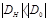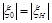Из этого соотношения ясно, что если точка возбуждения лежит на (в этом случае =0), то . Если же она лежит на гиперболической поверхности, то при очевидно, что , при и .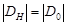

При дальнейшем сдвиге вдоль гиперболы 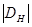становится больше 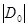. Наконец, если точка А переходит на 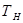, остается одна волн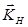а , а 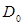=0. Отсюда очевидна относительность представления волны в качестве первичной, а 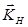- отраженной. Можно рассматривать волну 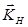в качестве первичной, а волна в направлении тогда будет отраженной той же системой плоскостей.

После подстановки (1.13) в уравнении (1.12) очевидно, что соотношение фаз волн и 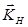определяется азимутом комплексных чисел 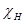и 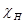и знаком вещественной величины 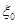(или 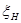). Следовательно, для волновых полей, точки возбуждения которых лежат на какой-либо из ветвей дисперсионной поверхности, (для данного состояния поляризации), соотношение фаз волн и 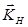. постоянно и меняется на π при переходе с одной ветви на другую, т.к. в этом случае меняются знак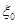и и .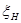

Важнейшую роль в динамической теории рассеяния играет понятие вектора потока энергии волнового поля :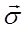

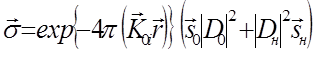(1.16)

где 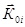- мнимая часть волнового вектора , характеризующая затухание поля, 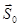( 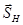) – единичные векторы, параллельные и 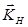. Здесь первый сомножитель описывает затухание волнового поля в кристалле.

Очевидно, что 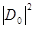и 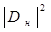- компоненты векторы 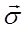в системе координат, оси которой параллельны и 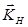. Но из (2-14) следует, что

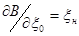, а .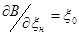

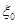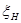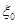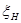Следовательно, и являются компонентами вектора grad B в системе координат, где и параллельны соответственно и 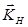. Очевидно, что отношение координат вектора grad B, нормального к кривой 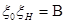в данной точке, равно согласно (2-16), отношению компонент вектора :

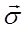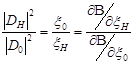
Очевидно, что компоненты векторов 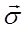и grad B пропорциональны в системах координат с параллельными осями, следовательно, сами векторы параллельны.

Направление потока энергии волнового поля совпадает с направлением нормали к дисперсионной поверхности в точке возбуждения данного волнового поля. Из определения (1.5) очевидно, что амплитуда волнового поля в общем случае представляет трехмерно периодическую функцию координат (блоховская волна).

Для двухволнового поля:

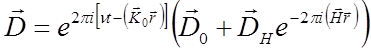(1.5а)

Очевидно, что положение максимумов (или минимумов) этой волны зависит от разносит фаз волн и 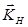(см. 2-12). Во всяком случае геометрическое место точек постоянного значения амплитуды 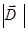параллельно плоскостям, описываемым уравнениям

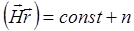, (n – целые числа), с межплоскостным расстоянием .

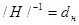Рассмотрим конкретных пример. Пусть точка возбуждения определяется координатами 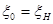. В этом случае 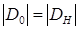. Пусть, как это имеет место, например для Si и отражения с индексами 220, структурная амплитуда вещественная величина (если пренебречь поглощением). В этом случае 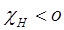(2-6а) (т.е., записав в общем случае комплексную величину 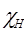в виде 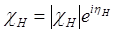, получаем в нашем случае 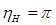. Тогда для первой ветви дисперсионной поверхности ( 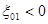) разница фаз между 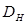и 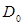согласно (1.12) равна нулю, т.е. волны 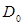и 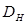по фазе совпадают, а для 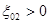разница фаз 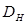и 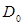равна π и волны находятся в противофазе. В соответствии с (1.5а) амплитуда первого поля:

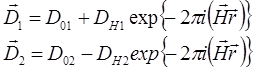- второго

(минус соответствует разности фаз π).

В тех точках кристалла, где 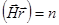, (n=0, 1, 2…).

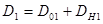, а 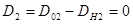. Наоборот, в точках, где

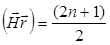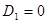, , а .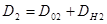

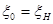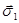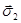На рисунке 3а показано направление потоков энергии и структура волновых полей первого и второго типа. При векторы и параллельны атомным плоскостям. Поглощения волнового поля определяется вероятностью фотоэффекта и пропорционально .

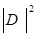Очевидно, поле первого типа в тех точках кристалла, где проекции на нормаль к отражающим плоскостям равна 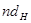, поглощается аномально сильно, а поле второго типа, у которого на атомных плоскостях располагаются узлы стоячей волны и пучности между плоскостями поглощается аномально слабо. Эффект аномально слабого поглощения блоховской волны при ее прохождении в кристалле называют эффектом Бормана.

Если точка возбуждения лежит так, ч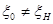то , то .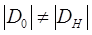

На рис. 3б показана структура блоховских волн и направление потоков энергий для первого и второго полей. В этих случаях векторы 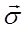не параллельны атомным плоскостям и различие в поглощении меньше для полей первого и второго типов.

В реальном эксперименте описанные выше волновые поля возбуждаются в ограниченных по размерам кристаллах внешней падающей на кристалл волной.

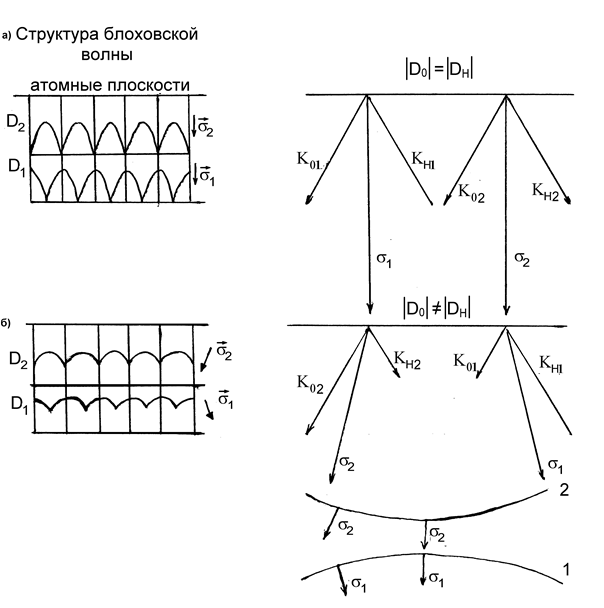
Рисунок 3 -Напрвление потоков энергии по отношению к атомным плоскостям.

Дата добавления: 2014-08-09; просмотров: 437; Нарушение авторских прав

Мы поможем в написании ваших работ!