Волновые поля в кристаллах

Для большого круга задач прикладного структурного анализа рассмотрение явления дифракции существенно упрощается, если предполагать, что интенсивность рассеянных волн много меньше интенсивности первичной волны, и не учитывать многократное рассеяние и сложное интерференционное взаимодействие падающей и рассеянных волн. Такой подход применяется для описания рассеяния на кристаллитах очень малых размеров, тонких слоях и кристаллитах с большой дефектностью. Характерные размеры L кристаллитов удовлетворяют при этом условию

l<<L<<L_э

где l– длина волны излучения,

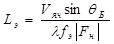
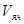– объем элементарной ячейки, q_б – брэгговский угол, 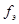– классический радиус электрона, равный ≈2,8*10^-13 см, 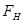– структурная амплитуда).

Этот подход не совсем подходит для описания дифракции рентгеновских лучей (РЛ) в почти совершенных кристаллах, большинство из которых представляет практический интерес для полупроводниковой промышленности. В кристаллах сравнительно совершенных периодичность распределения электронной плотности приводит к тому, что дифракция рентгеновских лучей является сложным процессом многократного рассеяния с перераспределением интенсивности из падающей волны в дифрагированную и обратно. Такой динамический процесс приводит к образованию в периодической структуре самосогласованного волнового поля. Поэтому соответствующая теория и называется динамической.

Схема возникновения такого волнового поля в кристалле показана на рис. 1. Если какая-либо волна с волновым вектором распространяется в кристалле и встречает под углами Брэгга одну или несколько систем атомных плоскостей, возникает одна или несколько отраженных волн. Волна с волновым вектором и отраженные от атомных плоскостей четное число раз когерентные волны составляют, интерферируя так называемый прямой пучок, прямую волну.

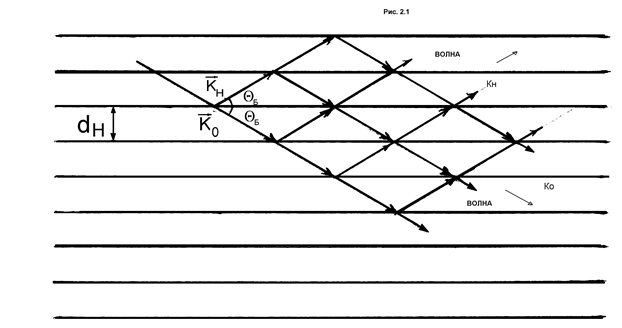
Рисунок 1 - Схема формирования волнового поля в идеальном кристалле при интерференции когерентных волн в случае, когда в отражающем положении находится одно семейство плоскостей.

Сложение когерентных волн, однократно или нечетное число раз отраженных от

какой-либо системы плоскостей, создает результирующую дифрагированную волну с волновым вектором 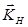, соизмеримую, в принципе, по амплитуде с прямой волной. Внутри кристалла значения волновых векторов должны удовлетворять закону сохранения импульса;

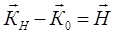(1.1)

где 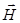– вектор обратной решетки (ОР), отражающей системы атомных плоскостей.

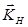Волны и когерентны и в кристалле образуют единое волновое поле. Коэффициент преломления этого поля зависит, очевидно, от совокупности интерферирующих волн, соотношения их амплитуд и фаз.

Волновой вектор прямой волны в кристалле отличается от волнового вектора 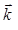в вакууме, отвечающего падающей на кристалл волне:

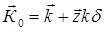(1.2)

Где 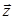– единичный вектор нормали к поверхности кристалла, d- коэффициент аккомодации, d‹‹1.

Распространение электромагнитных волн в любой среде можно описать с помощью уравнений Максвелла. Уравнение для распространения электромагнитной волн в среде с периодически меняющейся поляризуемостью 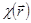предложил М. Лауэ [1]. При этом для рентгеновских частот электрическая проводимость в кристалле равна нулю, магнитная проницаемость в гауссовой системе единиц равна единице.

Вектор электрического поля рентгеновской волны, распространяющийся в кристалле, 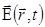и вектор ее электрической индукции 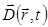связаны соотношением:

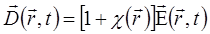(1.3)

где 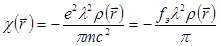- диэлектрическая восприимчивость для рентгеновского диапазона частот, 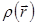- электронная плотность, 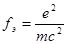- классический радиус электрона, m, е – масса и заряд электрона, с – скорость света.

Используя уравнение Максвелла, Лауэ получил уравнение, которому должна удовлетворять функция 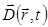в кристалле:

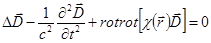(1.4)

Решение этого уравнения ищут в виде суперпозиции плоских волн:

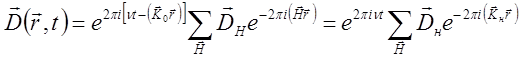(1.5)

где ν- частота колебания, 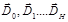– амплитуды когерентных волн, составляющих волновое поле. Суммирование проводится по всем векторам ОР 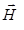. 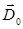можно рассматривать в качестве амплитуды первичной волны, 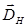– амплитуды волн, отраженных от атомных плоскостей, которым отвечают векторы .

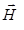Волны удовлетворяют условию, что векторы 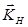и 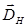взаимно ортогональны.

В периодической среде, идеальном кристалле, поляризуемость удобно представить в виде:

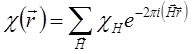(1.6)

где 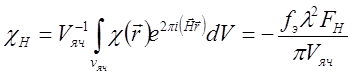(1.6а)

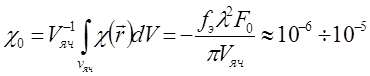(1.6б)

Подставив (1.5) и (1.6) в уравнение (1.4), Лауэ получил следующую систему уравнений.

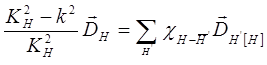(1.7)

где 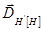- вектор, предоставляющий индукцию волн 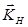, перпендикулярный вектору 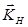, k – волновой вектор волны в вакууме

( ).

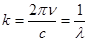Введем параметр:

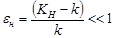(1.8)

Так как в общем случае правая часть уравнения (2-7) по порядку величины сохраняется, то малым значениям множителя

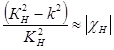
отвечают сильные плоские волны. В этом случае:

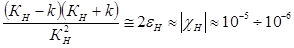
Воспользуемся построением Эвальда. Число узлов, лежащих вблизи сферы Эвальда (соответственно тому, что 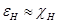) определяют число слагаемых в (1.7). Тем самым волновое поле состоит из нескольких сильных плоских волн, отвечающих отражениям только от тех плоскостей, узлы ОР которых практически лежат на сфере Эвальда, т.е. тех плоскостей, для которых выполняется условие (1.1).

Если первичная волна не отражается ни одной системой плоскостей и уравнение (1.1) не выполняется, тогда в кристалле распространяется только одна волна с волновым вектором .

В этом случае система (1.7) имеет вид:

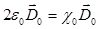или .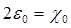

Учитывая определения (2-8) получаем для коэффициента преломления:

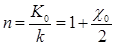(1.9)

независимо от поляризации вектора .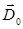

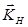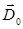Наибольший интерес с практической точки зрения представляет так называемое двухлучевое приближение. В этом приближении условию (1) удовлетворяет одна система плоскостей, и волновое поле является суперпозицией двух когерентных волн с волновыми векторами и амплитудами соответственно и , и .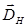

В правой части уравнения (2-5) остается лишь два слагаемых. Причем 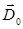и 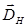в общем случае могут быть величинами одного порядка.

В этом случае систем (2-7) приобретает вид:

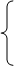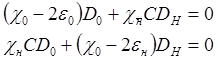(1.10)

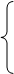
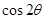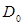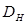, если и поляризованы в плоскости дифракции, π- поляризация.

Где С=

1, есл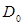и и 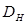перпендикулярны плоскости поляризации, 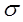-поляризация

Условие нетривиального решения имеет вид:

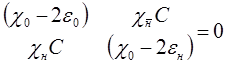(1.11)

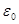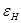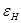Из уравнений (2-1) и (2-8) очевидно, что, при пренебрежении квадратами малых величин и , является линейной функцией .

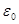Поэтому уравнение (2-11) является квадратным уравнением относительно 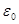(или 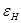) . Следовательно имеются для каждого состояния поляризации два значения 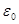, т.е. 2 значения и .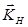

Из уравнений (2-10) легко получить отношение амплитуд волн составляющих волновое поле:

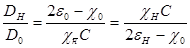(1.12)

Уравнение называют фундаментальным уравнением динамической теории. Они позволяют рассчитывать волновые поля внутри кристалла.

Очевидно, что в периодической среде, если выполняется условие (1.1) , для каждого состояния поляризации могут распространяться два волновых поля, удовлетворяющие уравнению (1.10).

Каждое поле характеризуется своим коэффициентом преломления и отношением амплитуд .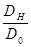

Эти два волновых поля существенно отличаются по своим характеристикам. Связь между характеристиками полей и условиями отражения волны от какой-либо системы плоскостей удобно демонстрировать с помощью так называемой дисперсионной поверхности.

Дата добавления: 2014-08-09; просмотров: 504; Нарушение авторских прав

Мы поможем в написании ваших работ!