Уравнения Лагранжа 2-го рода

Одним из преимуществ аналитической механики является использование обобщенных координат.

Обобщенными координатами механической системы называются независимые между собой параметры q₁, q₂, …, q_S любой размерности, однозначно определяющие положение системы в любой момент времени.

Число обобщенных координат равно S – числу степеней свободы механической системы. Положение каждой ν-й точки системы, то есть ее радиус вектор в общем случае всегда можно выразить в виде функции обобщенных координат:

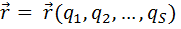(24)

Общее уравнение динамики в обобщенных координатах выглядит в виде системы S уравнений следующим образом:

;

;

……..………. ;

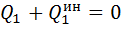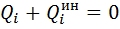(25)

………..……. ;

,

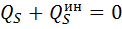здесь – обобщенная сила, соответствующая обобщенной координате :

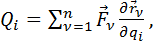(26)

а – обобщенная сила инерции, соответствующая обобщенной координате :

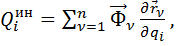(27)

Уравнения Лагранжа 2-го рода выводятся из общего уравнения динамики в обобщенных координатах. Число уравнений соответствует числу степеней свободы:

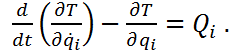(28)

Для составления уравнения Лагранжа 2-го рода выбираются обобщенные координаты 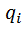и находятся обобщенные скорости 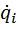. Находится кинетическая энергия системы, которая является функцией обобщенных скоростей, и, в некоторых случаях, обобщенных координат. Выполняются операции дифференцирования кинетической энергии, предусмотренные левыми частями уравнений Лагранжа.Полученные выражения приравниваются обобщенным силам, для нахождения которых помимо формул (26) часто при решении задач используют следующие:

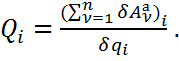(29)

В числителе правой части формулы – сумма элементарных работ все активных сил на возможном перемещении системы, соответствующем вариации i-й обобщенной координаты – 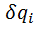. При этом возможном перемещении все остальные обобщенные координаты не изменяются. Полученные уравнения являются дифференциальными уравнениями движения механической системы с S степенями свободы.

3. Задания

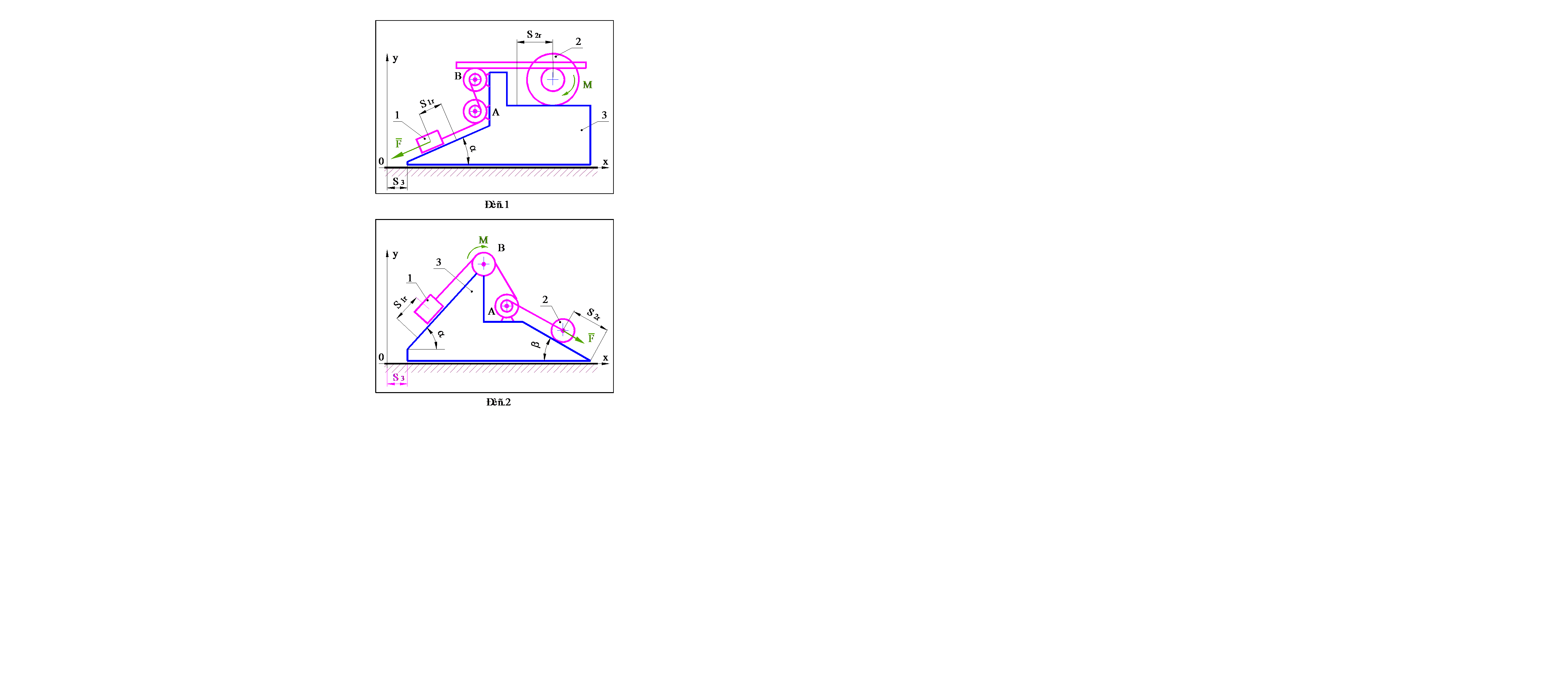
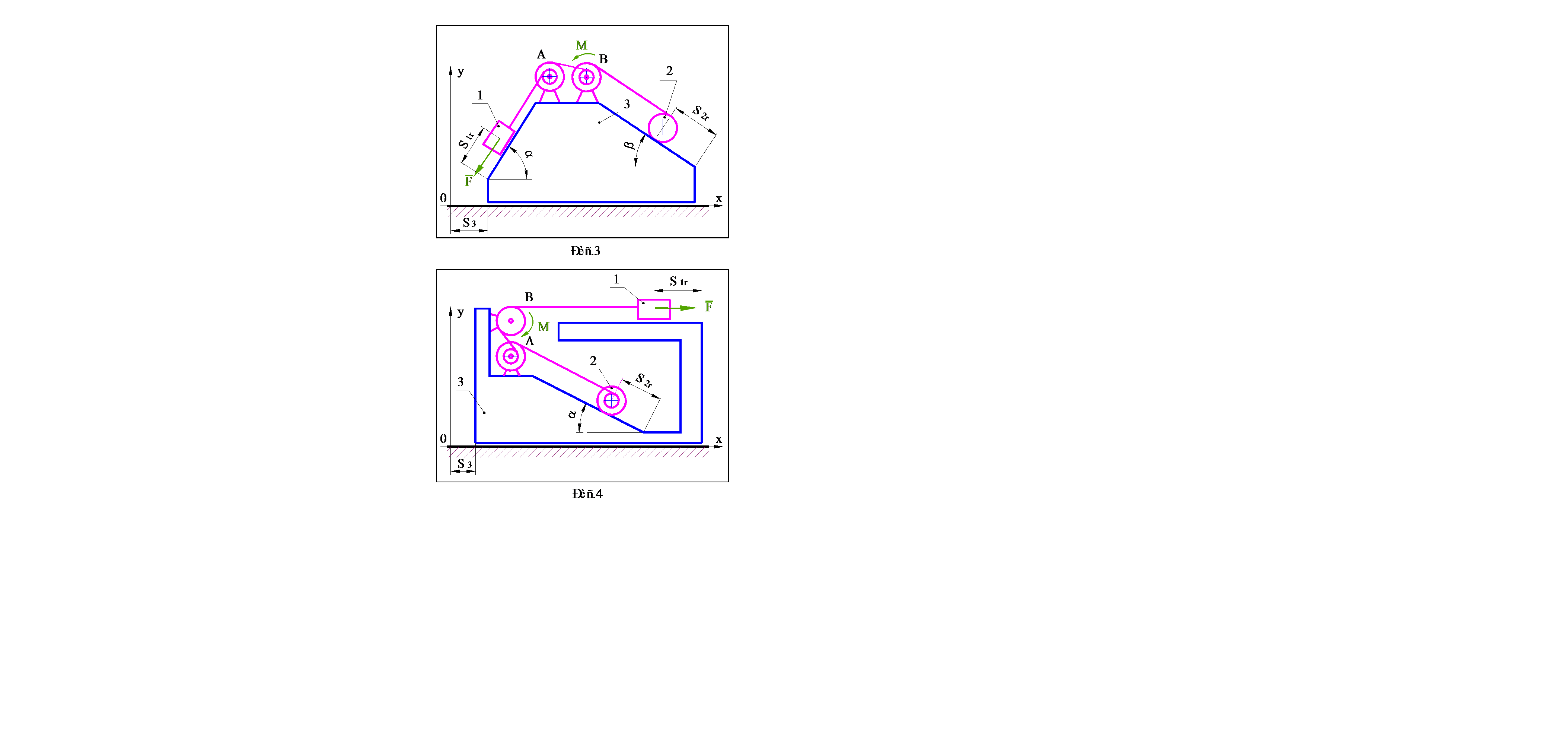
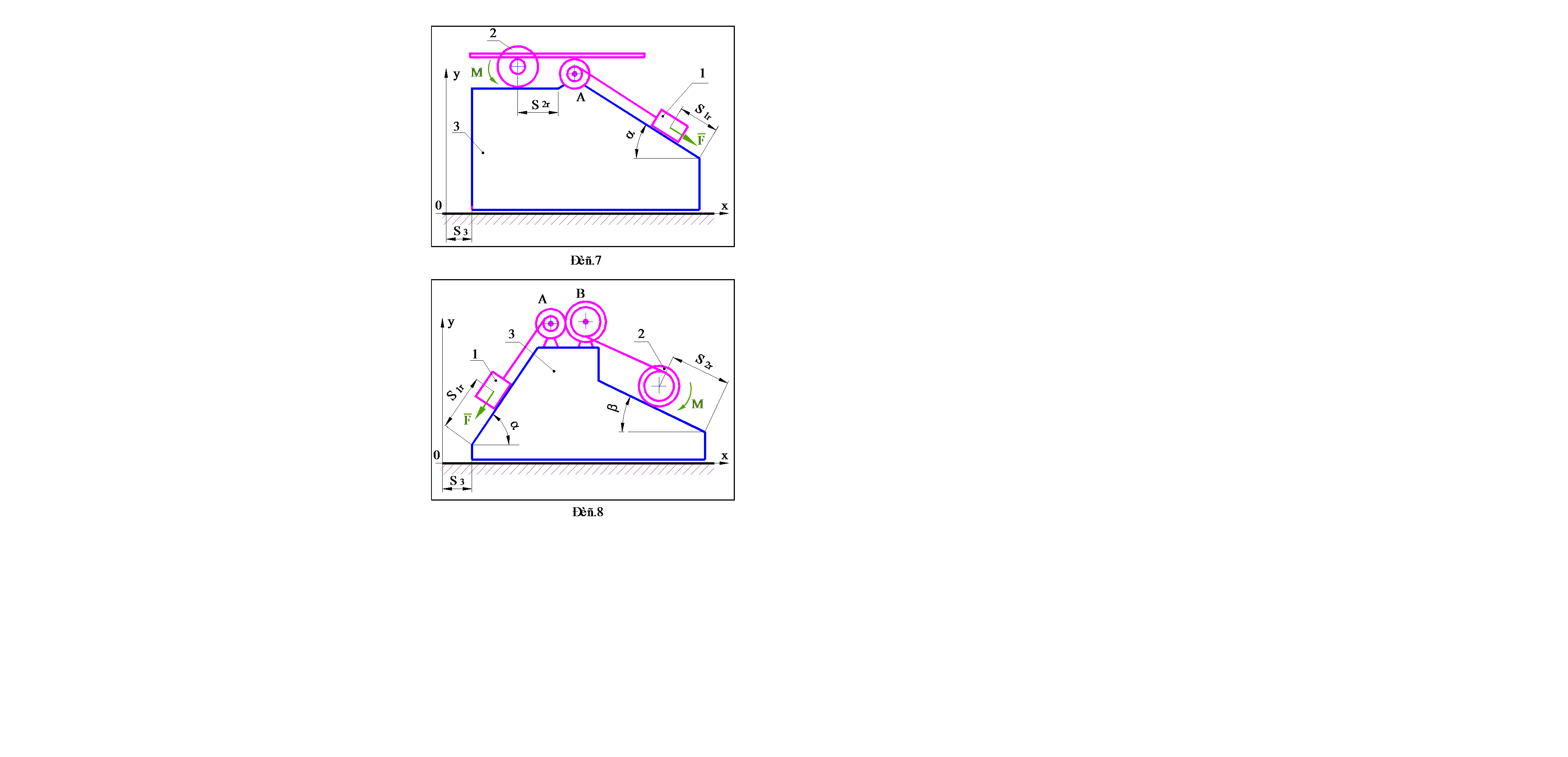
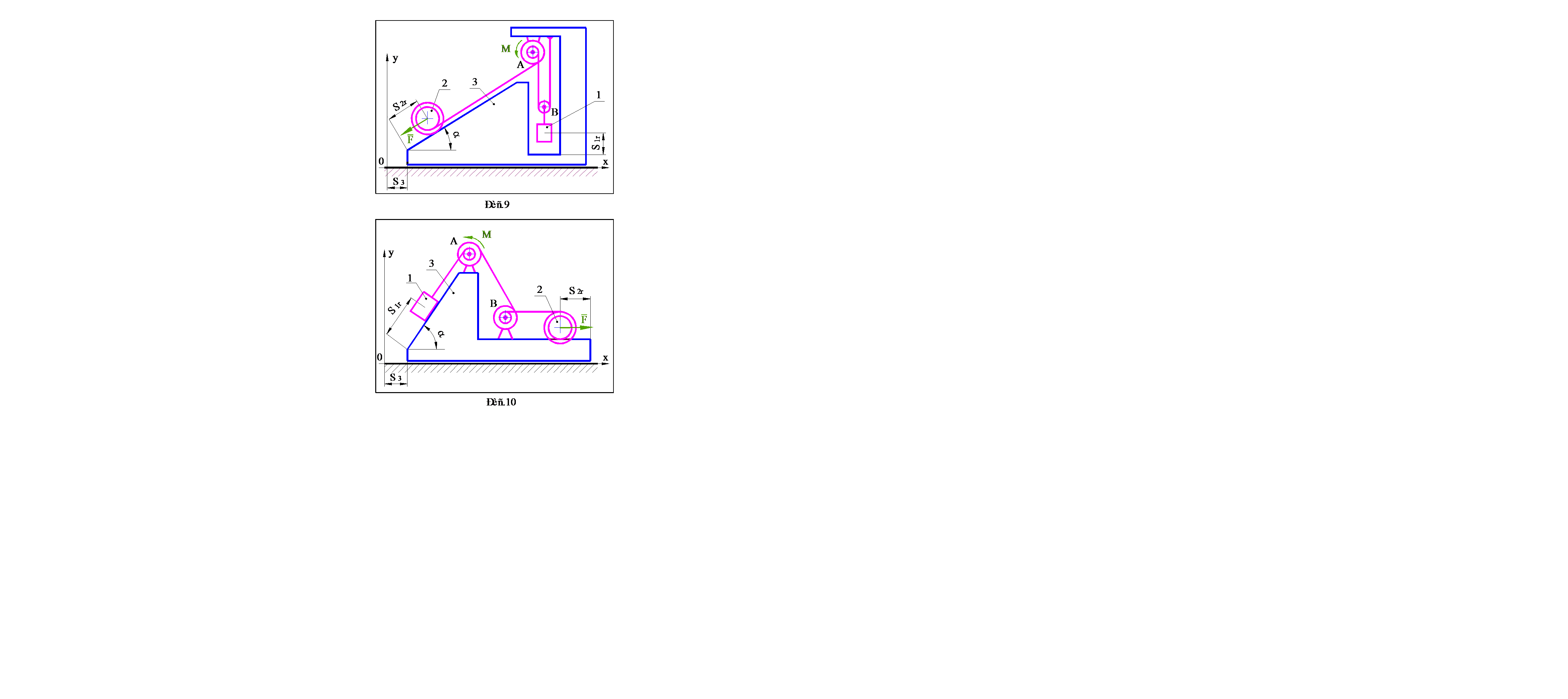
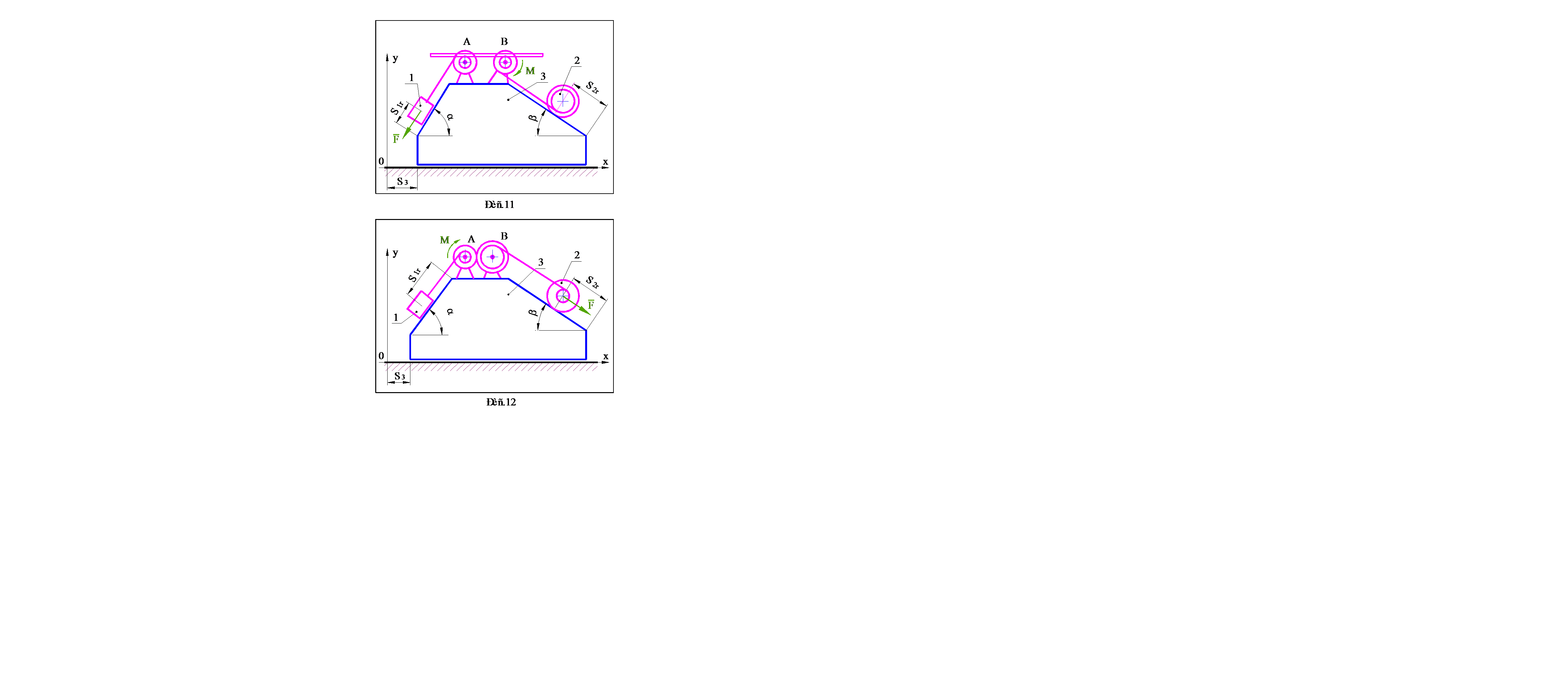
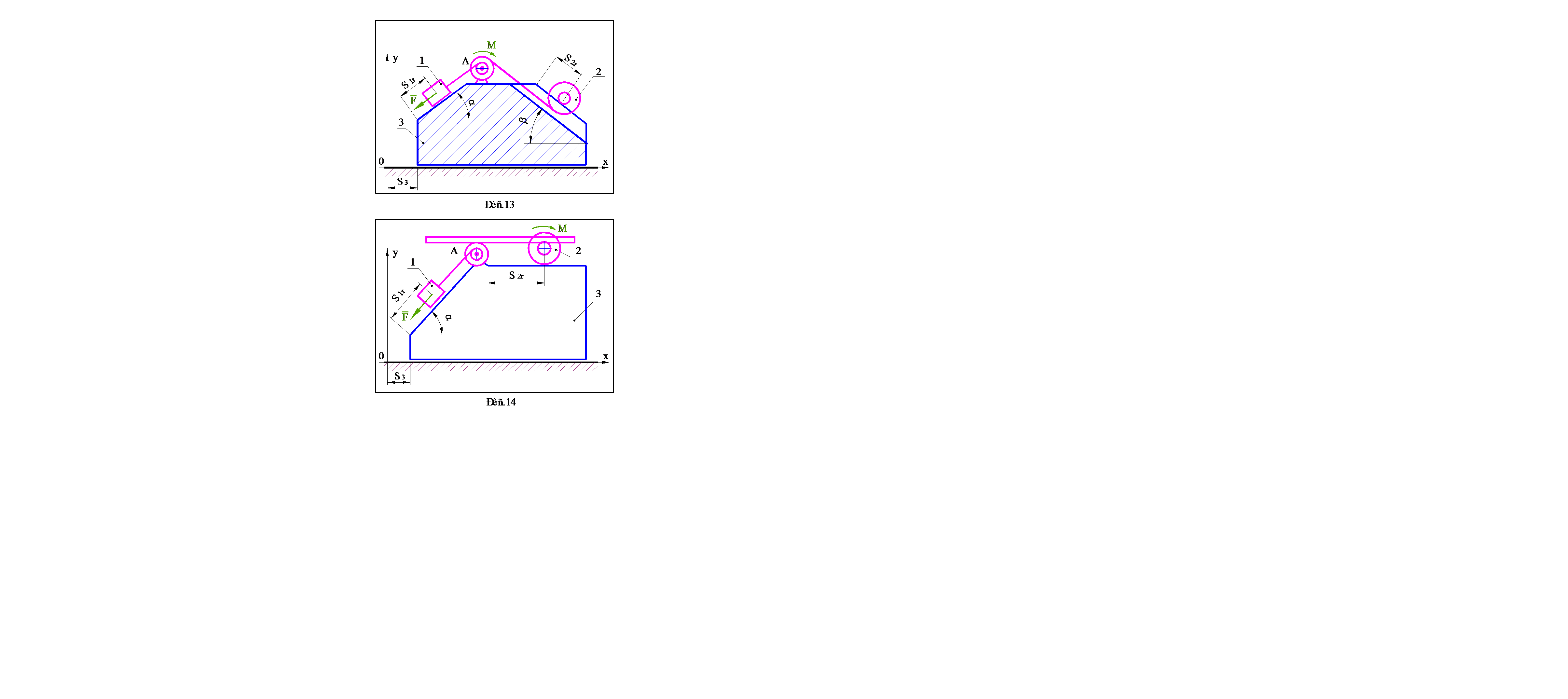
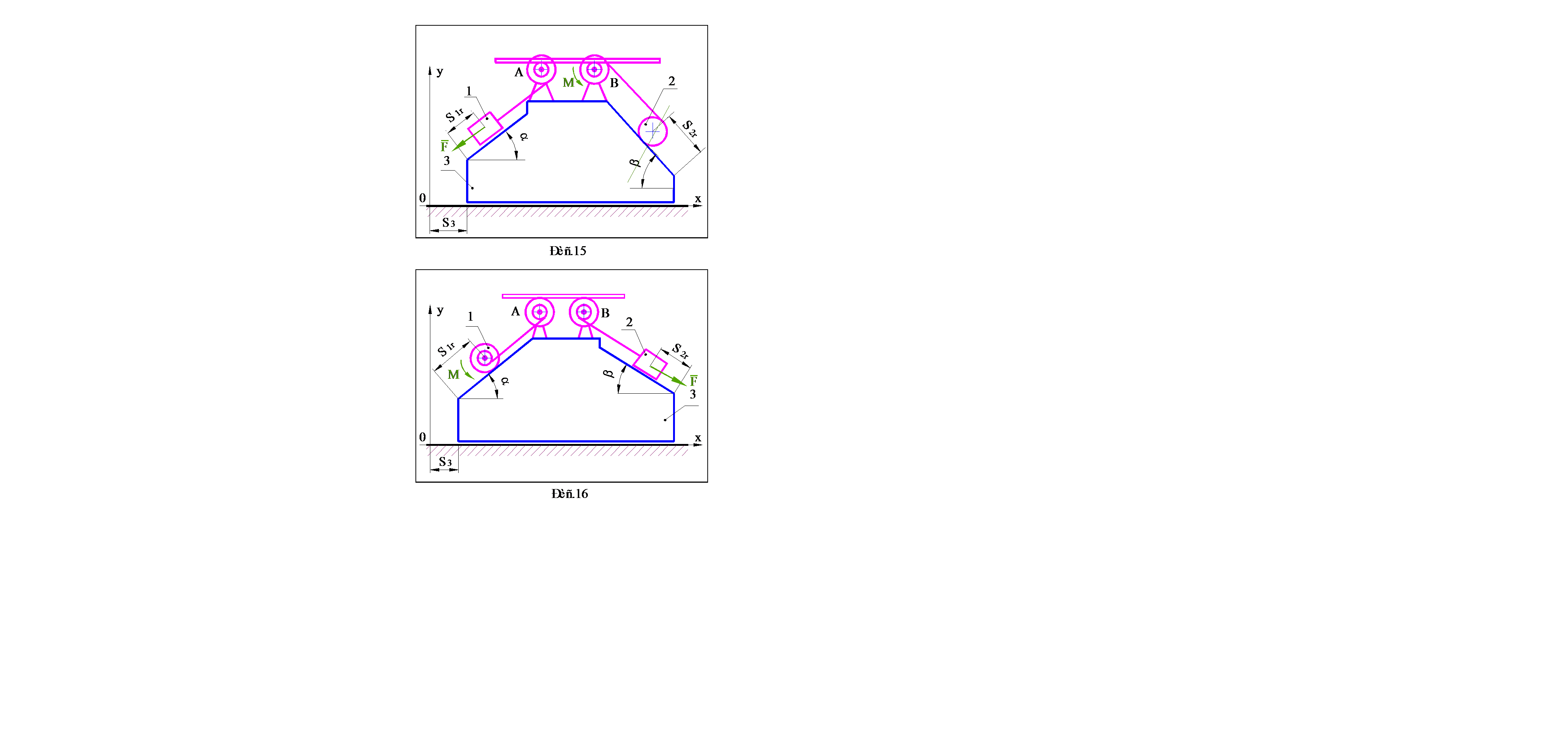
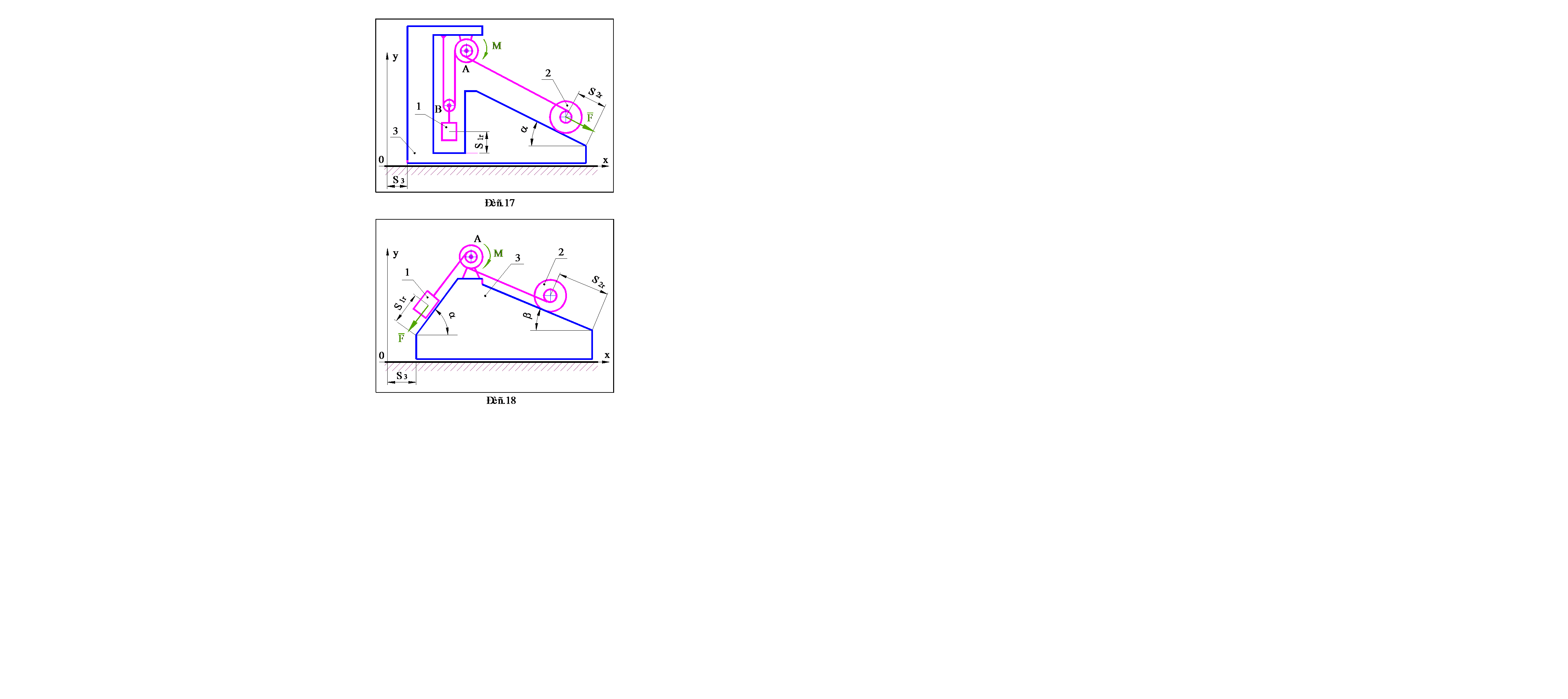
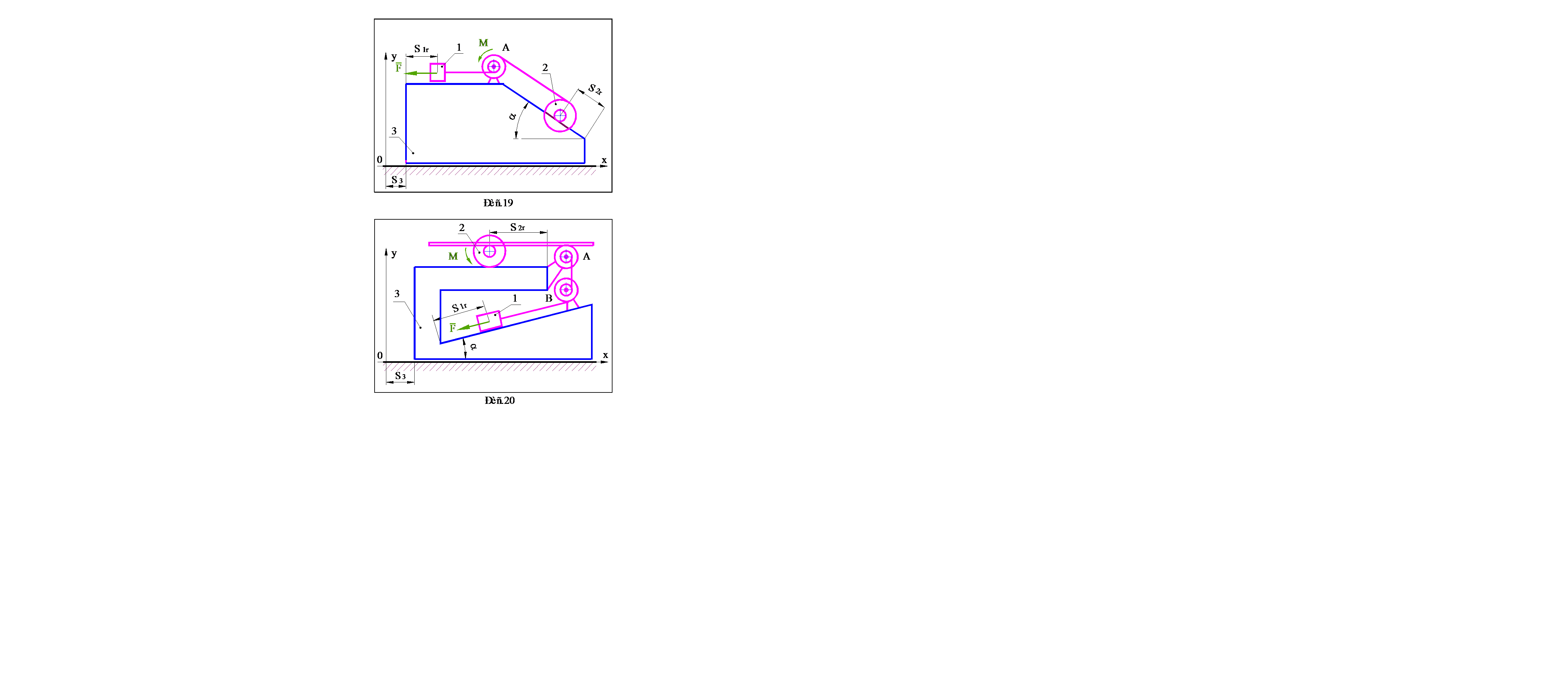
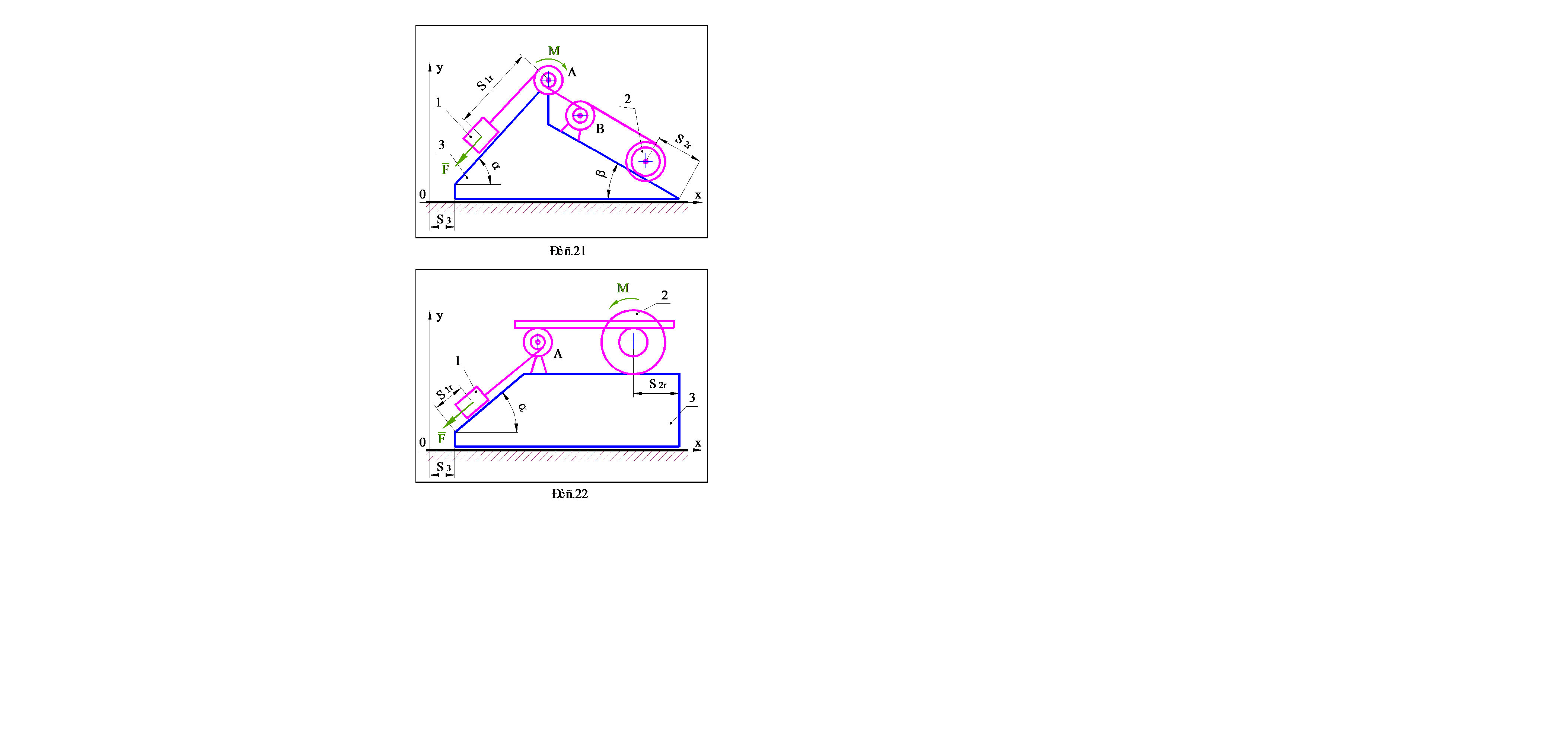
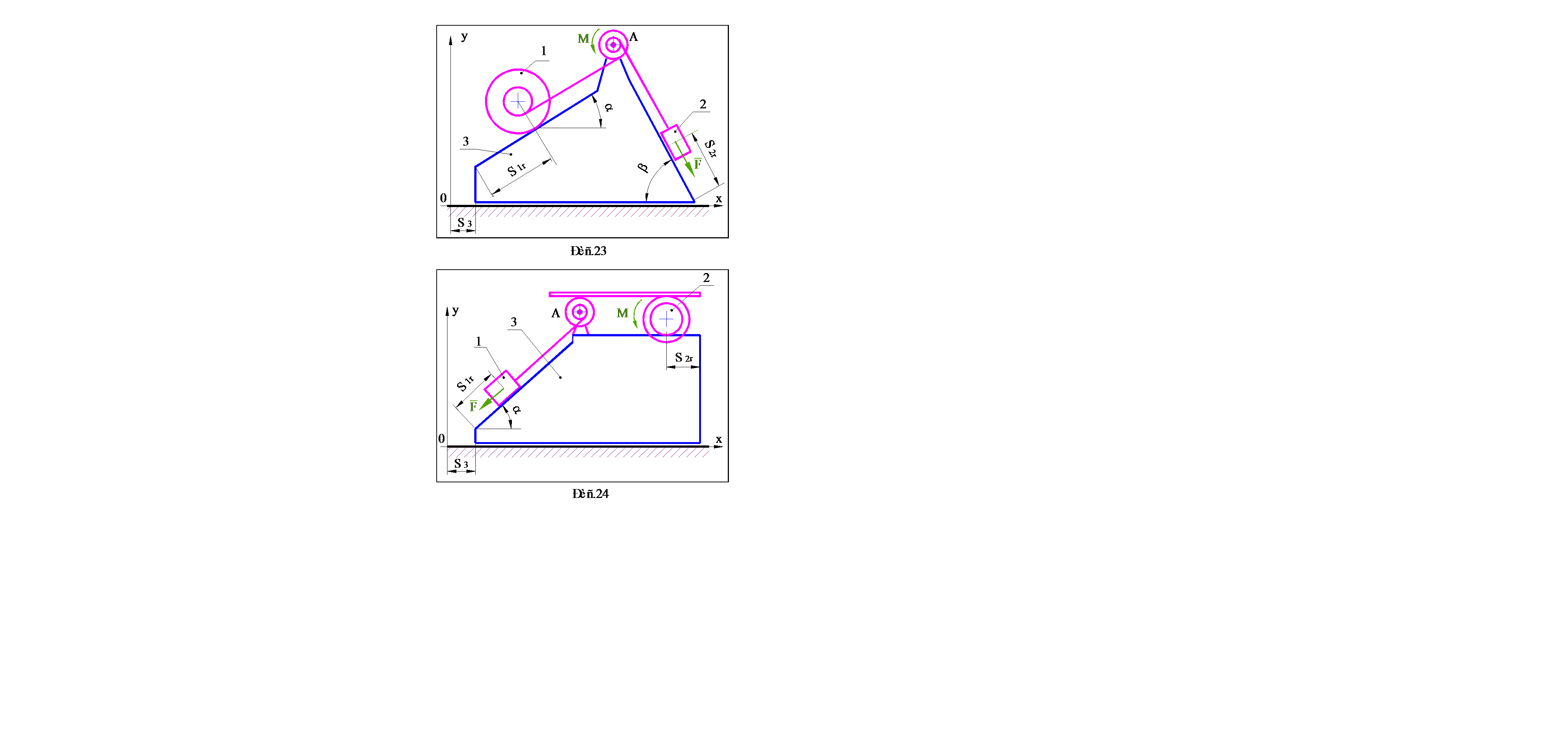
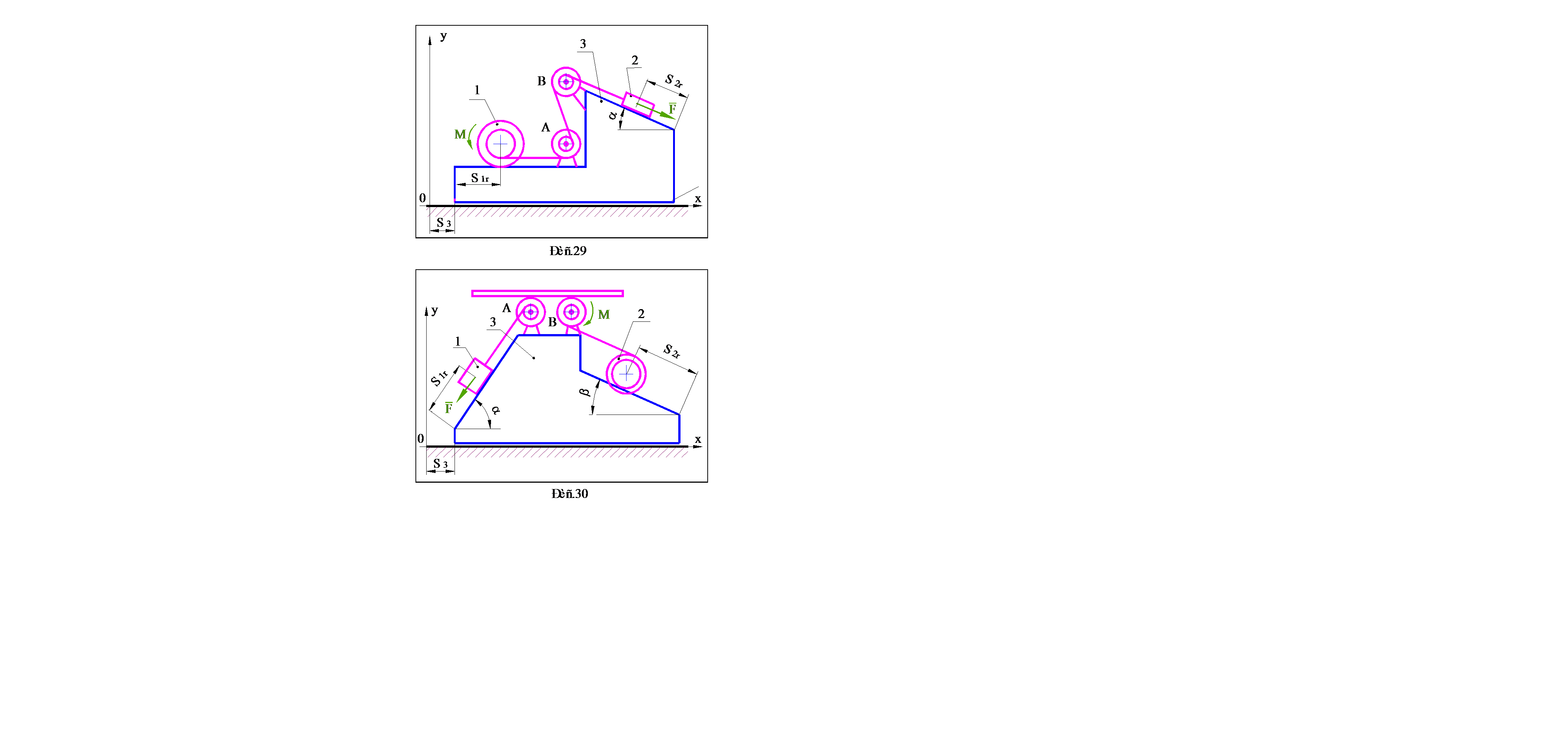
Варианты заданий выдаются преподавателем. Схемы механических систем представлены на рис.1–30, номера которых соответствуют номерам вариантов. Исходные данные, необходимые для решения, содержатся в таблице 1 (стр.31–32). Параметры, подлежащие определению, указываются в разделе 4, в котором приведена методика выполнения работы.

При решении задач учесть следующее:

· При выполнении пунктов 4.1 - 4.3, механической системой считать расположенную на идеально гладкой поверхности призму 3 и находящиеся на ней блоки A и B, а также тела 1 и 2, одно из которых скользит по поверхности призмы, а второе (каток) катится без проскальзывания. Движение системы считать происходящим только за счет сил тяжестей тел, составляющих систему, а показанные на рисунках силу F и момент M исключить.

· При выполнении пунктов 4.4 - 4.8, в качестве механической системы рассматривать тела, находящиеся на призме, а саму призму считать неподвижным основанием. Помимо сил тяжестей тел учитывать действие силы F и момента M .

· Радиусы инерции блоков и катков вычислять по формуле ;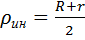

· Коэффициент трения качения для катка определять как ;

· Каток катиться без проскальзывания, коэффициент трения сцепления катка подлежит определению при решении задачи;

· Коэффициент трения скольжения тела (1 или 2), которое движется по призме 3 поступательно, принять f = 0,1;

· Нити невесомы и нерастяжимы;

· Зубчатые рейки невесомы.

Дата добавления: 2014-12-09; просмотров: 439; Нарушение авторских прав

Мы поможем в написании ваших работ!