
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Измерительные шкалы
В основе любого наблюдения и анализа лежат измерения. Измерение - это алгоритмическая операция, которая данному наблюдаемому состоянию объекта ставит в соответствие определенное обозначение: число, номер или символ. Обозначим через хi. i=1,…, m наблюдаемое состояние (свойство) объекта, а через уi, i = 1,..,m - обозначение для этого свойства. Чем теснее соответствие между состояниями и их обозначениями, тем больше информации можно извлечь в результате обработки данных. Менее очевидно, что степень этого соответствия зависит не только от организации измерений (т. е. от экспериментатора), но и от природы исследуемого явления, и что сама степень соответствия в свою очередь определяет допустимые (и недопустимые) способы обработки данных.
Свойство – философская категория, характеризующая такую сторону объекта (процесса или явления), которая обуславливает его различие или общность с другими объектами (процессами или явлениями). Свойство – категория качественная.
Множество обозначений, используемых для регистрации состояний наблюдаемого объекта, называется измерительной шкалой. Для измерения различных свойств объектов применяют различные шкалы. В общем случае под шкалойпонимается упорядоченное множество проявлений свойств объекта (качественных или количественных), отображенное на упорядоченное множество чисел или других условных знаков.
Измерительные шкалы в зависимости от допустимых на них операций различаются по их силе. Самые слабые - номинальные шкалы, а самые сильные - абсолютные.
●Шкала физических величин – это упорядоченная последовательность значений физической величины, принятая по соглашению сторон на основании точных измерений.
С нормативной информацией о шкалах можно познакомиться в МИ 2365-96 «Шкалы измерительные» (методическая инструкция).
●Шкалирование представляет собой отображение какого-либо свойства объекта или явления в числовом множестве.
Можно сказать, что чем сильнее шкала, в которой производятся измерения, тем больше сведений об изучаемом объекте, явлении, процессе дают измерения. Поэтому так естественно стремление каждого исследователя провести измерения в возможно более сильной шкале. Однако важно иметь в виду, что выбор шкалы измерения должен ориентироваться на объективные отношения, которым подчинена наблюдаемая величина, и лучше всего производить измерения в той шкале, которая максимально согласована с этими отношениями. Можно измерять и в шкале более слабой, чем согласованная (это приведет к потере части полезной информации), но применять более сильную шкалу опасно: полученные данные на самом деле не будут иметь той силы, на которую ориентируется их обработка.
Выделяют три основных атрибута измерительных шкал, наличие или отсутствие которых определяет принадлежность шкалы к той или иной категории:
1. Упорядоченность данных означает, что один пункт шкалы, соответствующий измеряемому свойству, больше, меньше или равен другому пункту;
2. Интервальность пунктов шкалы означает, что интервал между любой парой чисел, соответствующих измеряемым свойствам, больше, меньше или равен интервалу между другой парой чисел;
3. Нулевая точка (или точка отсчета) означает, что набор чисел, соответствующих измеряемым свойствам, имеет точку отсчета, обозначаемую за ноль, что соответствует полному отсутствию измеряемого свойства.
Все шкалы можно разделить на 2 группы:
1. Качественные или неметрические шкалы, в которых отсутствуют единицы измерений (номинальная и порядковая шкалы);
2. Количественные или метрические (шкала интервалов, шкала отношений и абсолютная шкала).
Виды шкал:
1. Шкалы наименований (номинальная или классификационная)
Шкала представляет собой конечный набор обозначений для никак не связанных между собой состояний (свойств) объекта (рис. 1).
Здесь отсутствуют все главные атрибуты измерительных шкал, а именно упорядоченность, интервальность, нулевая точка.
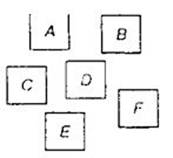
Рис. 1. Номинальная шкала.
Измерение будет состоять в том, чтобы, проведя эксперимент над объектом, определить принадлежность результата к тому или иному состоянию и записать это с помощью символа (набора символов), обозначающего данное состояние. Это самая простая шкала из тех, что могут рассматриваться как измерительные, хотя фактически эта шкала не ассоциируется с измерением и не связана с понятием «величина». Она используется только с целью отличить один объект от другого.
Номинальные шкалы применяются для объектов, свойства которых проявляются только в отношении эквивалентности .
Пр: атлас цветов, шкала запахов и т.п.
Допустимые операции, выполняемые с величинами:
= или ≠
Операции > или < недопустимы!
Если классифицируются дискретные по своей природе объекты и явления, то естественнее всего использовать шкалу наименований.
Примеры:
Для обозначения измеряемого (или оцениваемого) свойства в номинальной шкале могут быть использованы:
· слова естественного языка (например, географические названия, собственные имена людей и т. д.);
· произвольные символы (гербы и флаги государств, эмблемы родов войск, всевозможные значки и т.д.);
· номера (регистрационные номера автомобилей, официальных документов, номера на майках спортсменов);
· их различные комбинации (например, почтовые адреса, экслибрисы личных библиотек, печати и пр.).
Однако необходимость классификации возникает и в тех случаях, когда классифицируемые состояния образуют непрерывное множество (или континуум). Задача сводится к предыдущей, если все множество разбить на конечное число подмножеств, искусственно образуя тем самым классы эквивалентности; тогда принадлежность состояния к какому-либо классу снова можно регистрировать в шкале наименований. Однако условность введенных классов (не их шкальных обозначений, а самих классов) рано или поздно проявится на практике.
Примеры:
1. Например, возникают трудности точного перевода с одного языка на другой при описании цветовых оттенков: в английском языке голубой, лазоревый и синий цвета не различаются.
2. Названия болезней также образуют шкалу наименований. Психиатр, ставя больному диагноз «шизофрения», «паранойя», «маниакальная депрессия» или «психоневроз», использует номинальную шкалу; и все же иногда врачи не зря вспоминают, что «нужно лечить больного, а не болезнь»: название болезни лишь обозначает класс, внутри которого на самом деле имеются различия, так как эквивалентность внутри класса носит условный характер.
Необходимо понимать, что обозначения классов — это только символы, даже если для этого использованы номера. С этими номерами нельзя обращаться как с числами — это только цифры.
Пример: Если у одного спортсмена на спине номер 1, а другого — 2, то никаких других выводов, кроме того, что это разные участники соревнований, делать нельзя: например, нельзя сказать, что «второй в два раза лучше».
При обработке экспериментальных данных, зафиксированных в номинальной шкале, непосредственно с самими данными можно выполнять только операцию проверки их совпадения или несовпадения.
2. Шкала порядка (шкала рангов)
Она применяется в тех случаях, когда наблюдаемый (измеряемый) признак состояния имеет природу, не только позволяющую отождествить состояния с одним из классов эквивалентности, но и дающую возможность в каком-то отношении сравнивать разные классы. Порядковая шкала не имеет определенной количественной меры. При этом присутствует упорядоченность, но отсутствуют атрибуты интервальности и нулевой точки. Единственными типами отношений между неколичественными значениями шкалы могут быть:
а) равенство одинаковых значений порядковых переменных величин, соответствующих объектам одной категории,
б) неравенство разных значений переменных величин, соответствующих объектам одной категории;
в) отношения «больше» или «меньше» между разными значениями переменных величин, соответствующих объектам одной категории.
Измерение в шкале порядка может применяться, например, в следующих ситуациях:
- когда необходимо упорядочить объекты во времени или пространстве. Это ситуация, когда интересуются не сравнением степени выраженности какого-либо их качества, а лишь взаимным пространственным или временным расположением этих объектов;
- когда нужно упорядочить объекты в соответствии с каким-либо качеством, но при этом не требуется производить его точное измерение;
- когда какое-либо качество в принципе измеримо, но в настоящий момент не может быть измерено по причинам практического или теоретического характера.
Типовые порядковые шкалы
Обозначив такие классы символами и установив между этими символами отношения порядка, мы получим шкалу простого порядка:
А → В → C → D → E → F.
Примеры: Нумерация очередности, призовые места в конкурсе, социально-экономический статус («низший класс», «средний класс», «высший класс»).
Характерной особенностью порядковых шкал является то, что отношение порядка ничего не говорит о дистанции между сравниваемыми классами. Поэтому порядковые экспериментальные данные, даже если они изображены цифрами, нельзя рассматривать как числа. Например, нельзя вычислять выборочное среднее порядковых измерений.
Если свойство объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию, то количественно охарактеризовать это свойство можно по шкале порядка.
Особенностями шкал порядка являются:
1. отсутствие единицы измерений, одинаковой для всего диапазона;
2. отсутствие точных математических зависимостей при переходе от одной шкалы порядка к другой;
3. отсутствие естественно нуля;
4. единицы измерений всегда бывают условными и приближенными.
Математические операции, выполняемые с величинами:
= или ≠, > или <
Нельзя складывать величины и точно перевести из одной шкалы в другую (только приближенно)
Пример:
1. Шкала землетрясений;
2. Шкала Бофорта – силы ветра (морского шторма);
3. Шкала для определения твердости по Бринеллю (HB),
по Роквеллу (HRC, HRB, HRA),
по Виккерсу (HV).
При обозначении твердости: HRC 58…62, НВ 230…280 обозначение шкалы «HRC» или «НВ» правильней писать перед величиной твердости, а не после, так как это не единица измерений.
Примеры:
1. Шкалы землетрясений
Магниту́да землетрясе́ния — величина, характеризующая энергию, выделившуюся при землетрясении в виде сейсмических волн. Первоначальная шкала магнитуды была предложена американским сейсмологом Чарльзом Рихтером в 1935 году, поэтому в обиходе значение магнитуды ошибочно называют шкалой Рихтера.
Распространённые заблуждения
Магнитуда характеризует землетрясение как цельное, глобальное событие и не является показателем интенсивности землетрясения, ощущаемой в конкретной точке на поверхности Земли. Интенсивность землетрясения, измеряемая в баллах, не только сильно зависит от расстояния до очага; в зависимости от глубины центра и типа горных пород сила землетрясений с одинаковой магнитудой может различаться на 2—3 балла.
Магнитуда — безразмерная величина, она не измеряется в баллах.
Правильное употребление: «землетрясение с магнитудой 6.0», «землетрясение силой в 5 магнитуд по шкале Рихтера»
Неправильное употребление: «землетрясение с магнитудой 6 баллов», «землетрясение силой 6 баллов по шкале Рихтера».
а) Шкала Рихтера
Рихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах) иглы стандартного сейсмографа Вуда-Андерсона, расположенного на расстоянии не более 600 км от эпицентра: ML = lgA + f, где f — корректирующая функция, вычисляемая по таблице в зависимости от расстояния до эпицентра. Увеличение магнитуды на 1,0 соответствует увеличению амплитуды колебаний в 10 раз и увеличению энергии примерно в 32 раза.
Эта шкала имела несколько существенных недостатков:
- Рихтер использовал для градуировки своей шкалы малые и средние землетрясения южной Калифорнии, характеризующиеся малой глубиной очага.
- Из-за ограничений используемой аппаратуры шкала Рихтера была ограничена значением около 6,8.
- Предложенный способ измерения учитывал только поверхностные волны, в то время как при глубинных землетрясениях существенная часть энергии выделяется в форме объёмных волн.
В течение следующих нескольких десятков лет шкала Рихтера уточнялась и приводилась в соответствие с новыми наблюдениями. Сейчас существует несколько производных шкал, самыми важными из которых являются:
б) Сейсмический момент и шкала Канамори
В 1977 году сейсмолог Хиро Канамори из Калифорнийского технологического института предложил принципиально иную оценку интенсивности землетрясений, основанную на понятии сейсмического момента.
Сейсмический момент землетрясения определяется как , где
В единицах СИ сейсмический момент имеет размерность Па × м² × м = Н × м.
Шкала Канамори хорошо согласуется с более ранними шкалами при 3 < M < 7 и лучше подходит для оценки крупных землетрясений.
Энергия землетрясения
В каком-то смысле различные способы измерения магнитуды землетрясений являются приближениями к «идеальной» энергетической шкале:
где E — энергия землетрясения в джоулях.
Сейсмическая энергия, выделяемая при ядерном взрыве мощностью 1 мегатонна, эквивалентна землетрясению с магнитудой около 6,0. Стоит заметить, что только небольшая часть энергии взрыва преобразуется в сейсмические колебания.
За год на Земле происходит примерно:
1 землетрясение с магнитудой 8,0 и выше;
10 — с магнитудой 7,0—7,9;
100 — с магнитудой 6,0—6,9;
1000 — с магнитудой 5,0—5,9.
12-балльная шкала силы ветра
2)Шкала Бофорта — двенадцатибалльная шкала, принятая Всемирной метеорологической организацией для приближенной оценки скорости ветра по его воздействию на наземные предметы или по волнению в открытом море. Средняя скорость ветра указывается на стандартной высоте 10 м над открытой ровной поверхностью.
Шкала разработана английским адмиралом Ф. Бофортом в 1806 году. С 1874 года принята для использования в международной синоптической практике. Первоначально в ней не указывалась скорость ветра (добавлена в 1926 году). В 1955 году, чтобы различать ураганные ветры разной силы, Бюро погоды США расширило шкалу до 17 баллов.Баллы Бофорта Словесное определение силы ветра Средняя скорость ветра, м/с (км/ч) Средняя скорость ветра, узлов Действие ветра
| Штиль | 0—0,2 (< 1) | 0—1 | Дым поднимается вертикально, листья деревьев неподвижны. Зеркально гладкое море | |
| Тихий | 0,3—1,5 (1—5) | 1—3 | Дым отклоняется от вертикального направления, на море лёгкая рябь, пены на гребнях нет. Высота волн до 0,1 м | |
| Легкий | 1,6—3,3 (6—11) | 3,5—6,4 | Ветер чувствуется лицом, листья шелестят, флюгер начинает двигаться, на море короткие волны максимальной высотой до 0,3 м | |
| Слабый | 3,4—5,4 (12—19) | 6,6—10,1 | Листья и тонкие ветки деревьев колышутся, колышутся лёгкие флаги, лёгкое волнение на воде, изредка образуются маленькие "барашки". Средняя высота волн 0,6 м | |
| Умеренный | 5,5—7,9 (20—28) | 10,3—14,4 | Ветер поднимает пыль, бумажки; качаются тонкие ветви деревьев, белые "барашки" на море видны во многих местах. Максимальная высота волн до 1,5 м | |
| Свежий | 8,0—10,7 (29—38) | 14,6—19,0 | Качаются ветки и тонкие стволы деревьев, ветер чувствуется рукой, на воде видны белые "барашки". Максимальная высота волн 2,5 м, средняя — 2 м | |
| Сильный | 10,8—13,8 (39—49) | 19,2—24,1 | Качаются толстые сучья деревьев, тонкие деревья гнутся, гудят телефонные провода, зонтики используются с трудом; белые пенистые гребни занимают значительные площади, образуется водяная пыль. Максимальная высота волн — до 4 м, средняя — 3 м | |
| Крепкий | 13,9—17,1 (50—61) | 24,3—29,5 | Качаются стволы деревьев, гнутся большие ветки, трудно идти против ветра, гребни волн срываются ветром. Максимальная высота волн до 5,5 м | |
| Очень крепкий | 17,2—20,7 (62—74) | 29,7—35,4 | Ломаются тонкие и сухие сучья деревьев, говорить на ветру нельзя, идти против ветра очень трудно. Сильное волнение на море. Максимальная высота волн до 7,5 м, средняя — 5,5 м | |
| Шторм | 20,8—24,4 (75—88) | 35,6—41,8 | Гнутся большие деревья, ветер срывает черепицу с крыш, очень сильное волнение на море, высокие волны (максимальная высота — 10 м, средняя — 7 м) | |
| Сильный шторм | 24,5—28,4 (89—102) | 42,0—48,8 | На суше бывает редко. Значительные разрушения строений, ветер валит деревья и вырывает их с корнем, поверхность моря белая от пены, сильный грохот волн подобен ударам, очень высокие волны (максимальная высота — 12,5 м, средняя — 9 м) | |
| Жестокий шторм | 28,5—32,6 (103—117) | 49,0—56,3 | Наблюдается очень редко. Сопровождается разрушениями на больших пространствах. На море исключительно высокие волны (максимальная высота — до 16 м, средняя — 11,5 м), суда небольших размеров временами скрываются из виду | |
| Ураган | > 32,6 (> 117) | > 56 | Серьёзные разрушения капитальных строений |
4)Шкала́ Мо́оса (минералогическая шкала твёрдости) — набор эталонных минералов для определения относительной твёрдости методом царапания. В качестве эталонов приняты 10 минералов, расположенных в порядке возрастающей твёрдости.
Предложена в 1811 году немецким минералогом Фридрихом Моосом.
Значения шкалы от 1 до 10 соответствуют 10 достаточно распространённым минералам от талька до алмаза. Твёрдость минерала измеряется путём поиска самого твёрдого эталонного минерала, который он может поцарапать; и/или самого мягкого эталонного минерала, который царапает данный минерал. Например, если минерал царапается апатитом, но не флюоритом, то его твёрдость находится в диапазоне от 4 до 5.
Предназначена для грубой сравнительной оценки твёрдости материалов по системе мягче-твёрже. Испытываемый материал либо царапает эталон и его твёрдость по шкале Мооса выше, либо царапается эталоном и его твёрдость ниже эталона. Таким образом, шкала Мооса информирует только об относительной твёрдости минералов. Например, корунд (9) в 2 раза твёрже топаза (8), но при этом почти в 4 раза менее твёрдый, чем алмаз (10).
В приведённой ниже таблице приведено соответствие твёрдости по шкале Мооса с абсолютной твёрдостью, измеренной склерометром.
| Твёрдость по Моосу | Эталонный минерал | Абсолютная твёрдость | Обрабатываемость | Другие минералы с аналогичной твердостью |
| Тальк (Mg3Si4O10(OH)2) | Царапается ногтем | Графит | ||
| Гипс (CaSO4·2H2O) | Царапается ногтем | Галит, хлорит | ||
| Кальцит (CaCO3) | Царапается медной монетой | Биотит, золото, серебро | ||
| Флюорит (CaF2) | Царапается ножом, оконным стеклом | Доломит, сфалерит | ||
| Апатит (Ca5(PO4)3(OH-,Cl-,F-)) | Царапается ножом, оконным стеклом | Гематит, лазурит | ||
| Ортоклаз (KAlSi3O8) | Царапается напильником | Опал, рутил | ||
| Кварц (SiO2) | Поддаётся обработке алмазом, царапает стекло | Гранат, турмалин | ||
| Топаз (Al2SiO4(OH-,F-)2) | Поддаётся обработке алмазом, царапает стекло | Берилл, шпинель | ||
| Корунд (Al2O3) | Поддаётся обработке алмазом, царапает стекло | |||
| Алмаз (C) | Режет стекло |
Помимо шкалы Мооса есть и другие методы определения твёрдости, но различные шкалы твёрдости нельзя однозначно соотнести друг с другом. Практикой приняты несколько более точных систем измерения твёрдости материалов, ни одна из которых не покрывает весь спектр шкалы Мооса.
3) Шкала интервалов (разностей)
применяется для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка, аддитивности.
Следующая по силе шкала - шкала интервалов (интервальная шкала), которая в отличие от предыдущих, качественных, шкал уже является количественной шкалой. Эта шкала применяется, когда упорядочивание значений измерений можно выполнить настолько точно, что известны интервалы между любыми двумя из них (рис. 2).

Рис. 2. Соотношение шкал интервалов для одной и той же физической величины.
В шкале интервалов присутствуют упорядоченность и интервальность, но нет нулевой точки. Шкалы могут иметь произвольные начала отсчета, а связь между показаниями в таких шкалах является линейной:
Примеры:
1. Температура, время, высота местности — величины, которые по физической природе либо не имеют абсолютного нуля, либо допускают свободу выбора в установлении начала отсчета.
2. Часто можно услышать фразу: «Высота ... над уровнем моря». Какого моря? Ведь уровень морей и океанов разный, да и меняется со временем. В России высоты точек земной поверхности отсчитывают от среднемноголетнего Уровня Балтийского моря в районе Кронштадта.
В этих шкалах присутствует условный 0, интервал равный для всей шкалы, условная единица измерений.
Примеры:
1. Шкала температур (не Кельвин)
Шкала шведского ученого Цельсия (в 1742г) 1 0С= 1/100 (разница t0 кипения и t0 замерзания воды),
Шкала Фаренгейта (в 1727г) 1 0F= 1/180 (разница t0 кипения и t0 замерзания воды),
Шкала Реомюра (в 1730г) 1 0R= 1/80 (разница t0 кипения и t0 замерзания воды),
Δt=1 0C=1,8 0F; 10F =5/90C
0 0C=+32 0F или 0 0F = -17.78 0C
t0C=5/9(t0F –32)
Возможен точный перевод из одной шкалы в другую
2. Шкала летосчисления в разных религиозных традициях
Примеры условного задания начала отсчета летосчисления или «0»:
· «0»в Христианском календаре – от рождества Христова, 0 год н.э. Но одновременно существует Юлианский календарь (введен Юлием цезарем), по которому живет православная церковь и Григорианский (введен в 1582г Папой римским Григорием ХIII), по которому живет Европа и Северная Америка.
· «0»в Иудаистском календаре – от сотворения мира 3760 г до н.э., год лунный, в году 354 (355) дней,
· «0»в Мусульманском календаре –622 год н.э. – от даты переселения пророка Мухаммеда из Мекки в Медин;
· «0»в Буддистском календаре – 543 г до н.э., год перехода Будды Гаутамы в Нирвану.
А возможно и от Большого взрыва или от возникновения планеты Земля (~4,5 млрд лет) и т.д.
Если основное уравнение измерений Q=q |Q|
То по шкале интервалов оно выглядит так
Q= Q 0 +q |Q| , где Q0 – начало отсчета.
Принципы построения шкалы интервалов:
1) Выбираются 2 реперные точки, которые назначаются условно, обычно они связаны с каким- то событием или состоянием.
1) Интервал между этими 2-мя точками делится на несколько частей, причем количество частей может быть произвольным.
2) Единица/интервал получаются естественно (год, сутки) или условно (неделя, градус Цельсия, градус по Фаренгейту), «0» – устанавливается условно (это одна из реперных точек).
Математические операции, выполняемые с величинами:
= или ≠ (эквивалентность); > или < (порядок)
+∆ или -∆ (аддитивность), но складывать и вычитать имеет смысл только интервалы значений, а не значения целиком.
Например:
1941г + 4г =1945г- это выражение имеет смысл,
а 1945г+1945г = 3990г – смысла не имеет.
| <== предыдущая страница | | | следующая страница ==> |
| | | Шкала отношений |
Дата добавления: 2014-02-27; просмотров: 1220; Нарушение авторских прав

Мы поможем в написании ваших работ!